食物链

食物链（3.15）

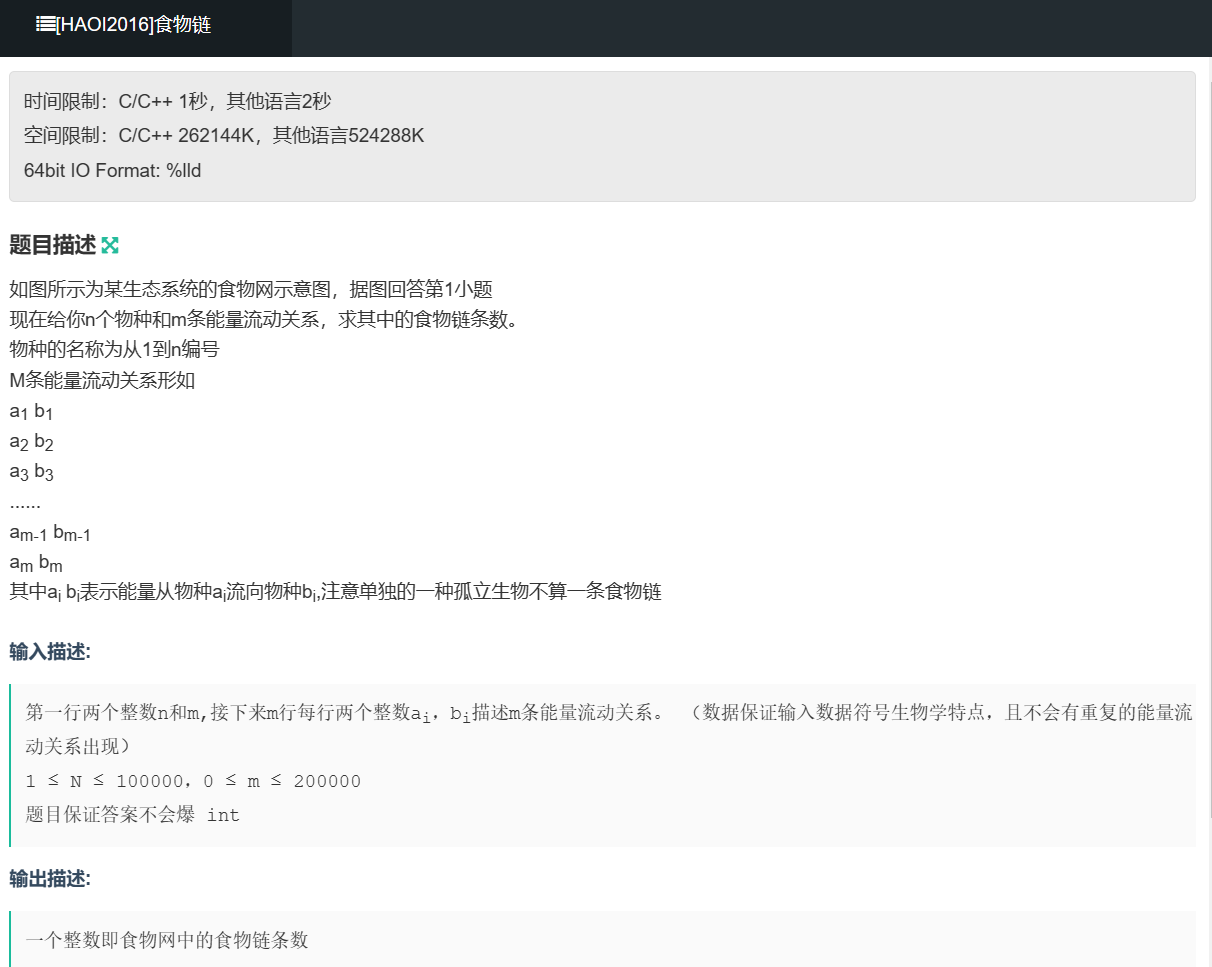
思路

1，拓扑排序

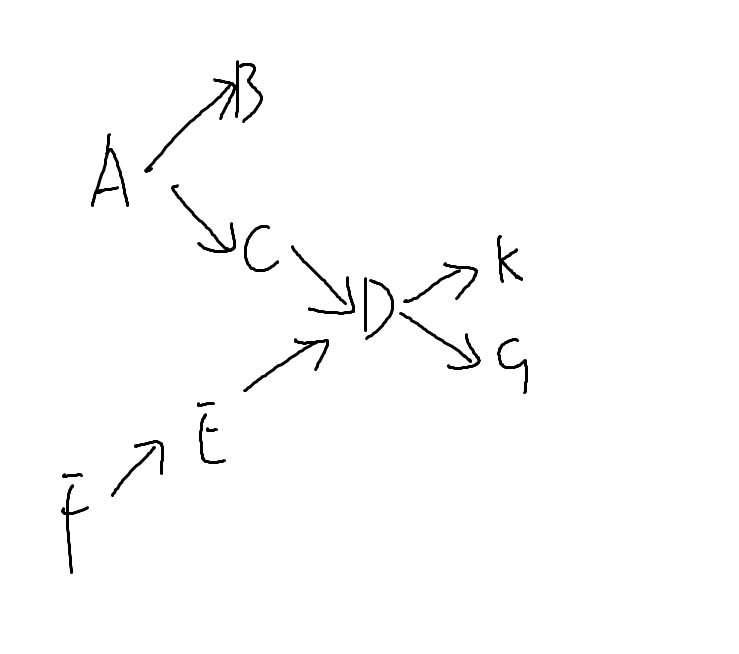
可以发现，食物网实则是一个有向无环图。
对食物链进行计数，就是看能到达"出口"，就是如图中\(K,G\)这样出度为\(0\)的点的路径数的总和。

在计数能到达一个点的路径数，实际上就是计数在它前一步的所有点的路径数的总和。
比如，图中到达点\(D\)的路径数，实际上就是到达点\(C,E\)的路径数的总和。

计数一个点的路径数前，必然是要先计数该点的前一步的点的路径数，这是存在一个先后顺序的。
实际上就是在进行拓扑排序，同时每个点会把路径数汇总到下一步的点。

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+5;

int n,m;

//in为入度,out为出度
int in[N],out[N];
//cnt[x]为到达x的路径数
int cnt[N];

//邻接表
vector<int>h[N];


int main()
{
    cin>>n>>m;
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        h[a].push_back(b);
        in[b]++;
        out[a]++;
    }
    
    //拓扑排序
    queue<int>q;
    for(int i=1;i<=n;i++)
    {
        //注意,单独一个点不计数
        //in[i]和h[i]都为0,说明该点为单独的点
        if(!in[i] && h[i].size()) 
        {
            q.push(i);
            cnt[i] = 1;
        }
    }
    while(q.size())
    {
        int t = q.front();
        q.pop();
        for(int i:h[t])
        {
            in[i]--;
            //把当前点t的路径数汇总到其下一步的点i的路径数中
            cnt[i]+=cnt[t];
            if(!in[i]) q.push(i);
        }
    }
    int ans = 0;
    for(int i=1;i<=n;i++)
    {
    	//食物链数量 = 到达出度为0的点的路径数的总和
        if(!out[i]) ans += cnt[i];
    }
    cout<<ans;
    
    return 0;
}

2，记忆化搜索

同样是这个图，换个角度考虑，可以去计数，从起点开始，可以延伸出多少条路径出来。

计数一个点能延伸出的路径数，实则就是计算它下一步的点能延伸出的路径数的总和。
比如图中的起点\(A\)，可以延伸出往点\(B\)和往点\(C\)的路径，点\(A\)能延伸的路径数就是点\(B,C\)能延伸出的路径数的总和。

可以发现，先计算下一步的点能延伸的路径数，再汇总回前一步的点，这是递归再回溯的过程，就是一个\(dfs\) 的过程。

但是，像图中点\(D\)这样的点，从起点\(A\)和从起点\(F\)开始\(dfs\)，它会被搜索多次，复杂度是会很高的。
可以对一个点能延伸出的路径数进行记忆化，开一个数组\(f[x]\)，记录点\(x\)能延伸出的路径数，这样就能保证每个点只会搜一次。

代码实现

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5+5;

int n,m;
//入度
int in[N];
//cnt[x]为点x能延伸出的路径数
int cnt[N];
//邻接表
vector<int>h[N];

int dfs(int u)
{
	//当搜到"出口"的时候,只可能有一条路径,返回1
    if(!h[u].size()) return 1;
    if(cnt[u]) return cnt[u];
    
    int res = 0;
    for(int i:h[u])
    {
    	//汇总下一步的点能延伸出的路径数
        res += dfs(i);
    }
    return cnt[u] = res;
}

int main()
{
    cin>>n>>m;
    while(m--)
    {
        int a,b;
        cin>>a>>b;
        h[a].push_back(b);
        in[b]++;
    }
    int ans = 0;
    for(int i=1;i<=n;i++)
    {
        if(!in[i])
        {
        	//如果入度为0,但没有下一步的点,说明是单独的点
            if(!h[i].size()) continue;
            ans += dfs(i);
        }
    }
    cout<<ans;
    
    return 0;
}