luogu P2233 [HNOI2002]公交车路线

[HNOI2002]公交车路线

题目描述

在长沙城新建的环城公路上一共有 $8$ 个公交站，分别为 A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行，因此你从某一个公交站到另外一个公交站往往要换几次车，例如从公交站 A 到公交站 D，你就至少需要换 $3$ 次车。

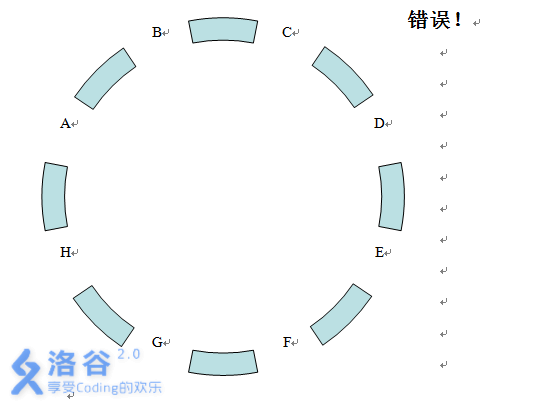
Tiger 的方向感极其糟糕，我们知道从公交站 A 到公交 E 只需要换 $4$ 次车就可以到达，可是 tiger 却总共换了 $n$ 次车，注意 tiger 一旦到达公交站 E，他不会愚蠢到再去换车。现在希望你计算一下 tiger 有多少种可能的乘车方案。

输入格式

仅有一个正整数 $n$，表示 tiger 从公交车站 A 到公交车站 E 共换了 $n$ 次车。

输出格式

输出一个正整数表示方案数，由于方案数很大，请输出方案数除以 $1000$ 后的余数。

样例 #1

样例输入 #1

6

样例输出 #1

8

提示

8 条路线分别是：

(A→B→C→D→C→D→E)，(A→B→C→B→C→D→E)，

(A→B→A→B→C→D→E)，(A→H→A→B→C→D→E)，

(A→H→G→F→G→F→E)，(A→H→G→H→G→F→E)，

(A→H→A→H→G→F→E)，(A→B→A→H→G→F→E)。

数据范围

$4\le n\le {10}^7$。

思路

显然我们两维状态dp[i][j]表示当前为第i次乘车 我们在第j个站
切记我们不可从E转移过去 所以我们的答案为dp[n-1][0]+dp[n-1][6]

#include <bits/stdc++.h>
using namespace std;
const int N = 1e7+10;
const int M = 998244353;
const int mod = 1000;
//#define int long long
#define endl '\n'
#define all(x) (x).begin(),(x).end()
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
#define _ 0
#define pi acos(-1)
#define INF 0x3f3f3f3f3f3f3f3f
#define fast ios::sync_with_stdio(false);cin.tie(nullptr);
int dp[2][7];
void solve() {
    int n;cin>>n;
    dp[0][3]=1;
    for(int i=1;i<n;i++){
        for(int j=0;j<7;j++){
            if(j==0)(dp[i&1][j]=dp[(i-1)&1][j+1])%=mod;
            else if(j==6)(dp[i&1][j]=dp[(i-1)&1][j-1])%=mod;
            else (dp[i&1][j]=dp[(i-1)&1][j-1]+dp[(i-1)&1][j+1])%=mod;
        }
    }
    cout<<(dp[n&1^1][0]+dp[n&1^1][6])%mod<<endl;
}
signed main(){
    fast
    int T;T=1;
    while(T--) {
        solve();
    }
    return ~~(0^_^0);
}

当然我们可以只考虑一边
但是这样我们和A和E一样属于端点 所以dp时要*2

#include <bits/stdc++.h>
using namespace std;
const int N = 1e7+10;
const int M = 998244353;
const int mod = 1000;
//#define int long long
#define endl '\n'
#define all(x) (x).begin(),(x).end()
#define YES cout<<"YES"<<endl;
#define NO cout<<"NO"<<endl;
#define _ 0
#define pi acos(-1)
#define INF 0x3f3f3f3f3f3f3f3f
#define fast ios::sync_with_stdio(false);cin.tie(nullptr);
int dp[2][4];
void solve() {
    int n;cin>>n;
    dp[0][0]=1;
    for(int i=1;i<n;i++){
        for(int j=0;j<4;j++){
            if(j==0)(dp[i&1][j]=2*dp[(i-1)&1][j+1])%=mod;
            else if(j==3)(dp[i&1][j]=dp[(i-1)&1][j-1])%=mod;
            else (dp[i&1][j]=dp[(i-1)&1][j-1]+dp[(i-1)&1][j+1])%=mod;
        }
    }
    cout<<(dp[n&1^1][3]*2)%mod<<endl;
}
signed main(){
    fast
    int T;T=1;
    while(T--) {
        solve();
    }
    return ~~(0^_^0);
}