完整教程:【Algorithm】Day-6
本篇文章主要讲解算法练习题
1 接雨水
题目描述:
给定
n个非负整数表示每个宽度为1的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。示例 2:
输入:height = [4,2,0,3,2,5] 输出:9提示:
n == height.length1 <= n <= 2 * 10^40 <= height[i] <= 10^5
题目解析:
这道题目的题意还是很好理解的,就是给你一个 height 数组,然后这个数组 height[i] 代表的是 i 下标位置柱子的高度,假设天空中下了一场大雨,问你这些柱子能存储多少格子的水量。比如:height = [1, 3, 4, 2, 0, 1, 2, 1, 0],用图来表示就是:
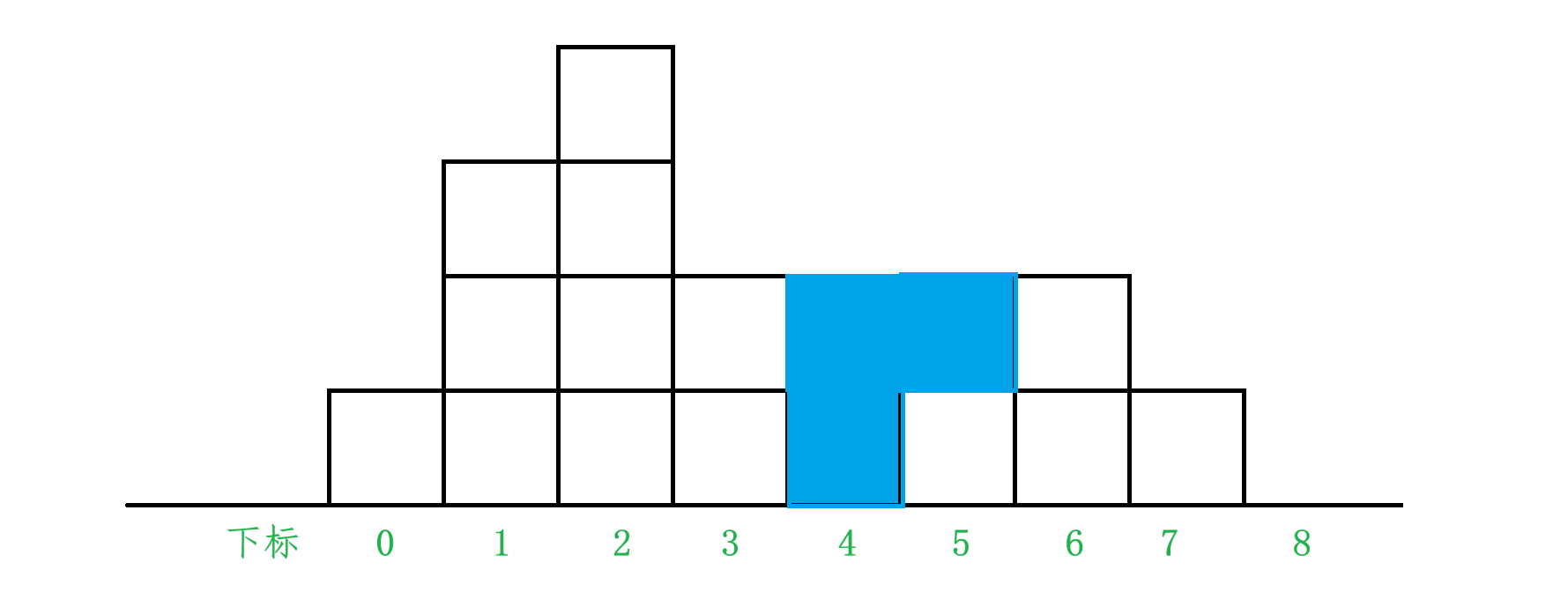
所以所能存储的水量就为3。
算法解析:
这道题目比较难,首先我们需要先想到一个办法,怎么能够求出总的水量呢?最简单的方法就是求出每根柱子上所能存储的水量,然后把每根柱子能存储的水量加起来,最后就是总的存水量了,那么怎么求出一个柱子的存水量呢?
我们可以模拟一下下雨时,下标为 i 的柱子是如何存水的:
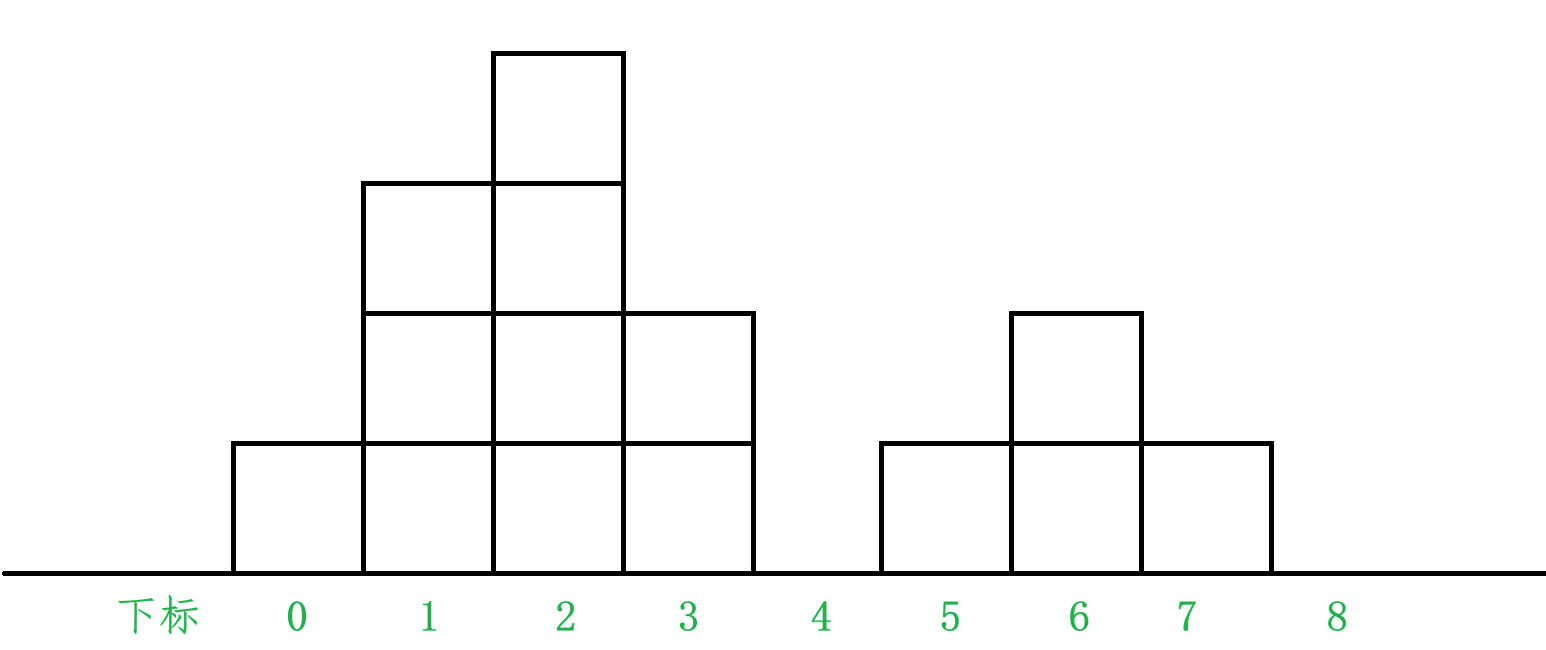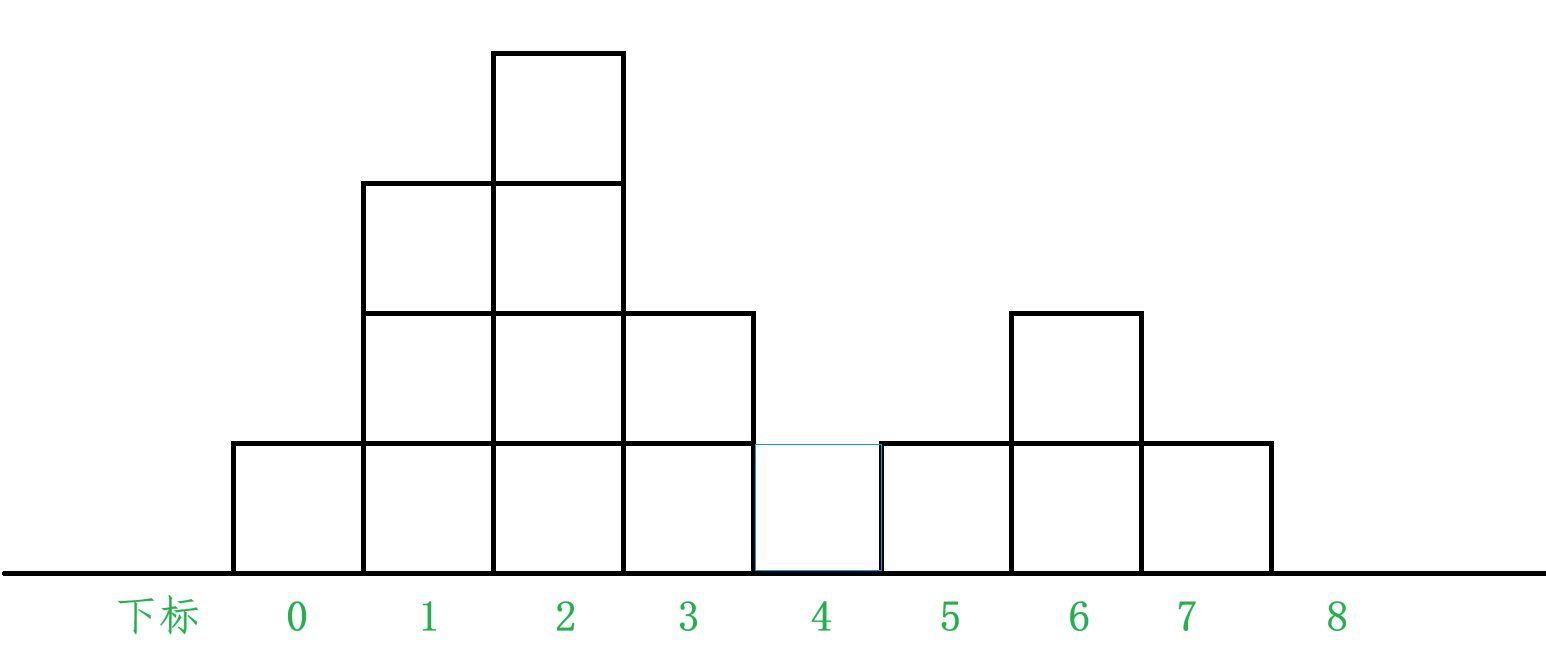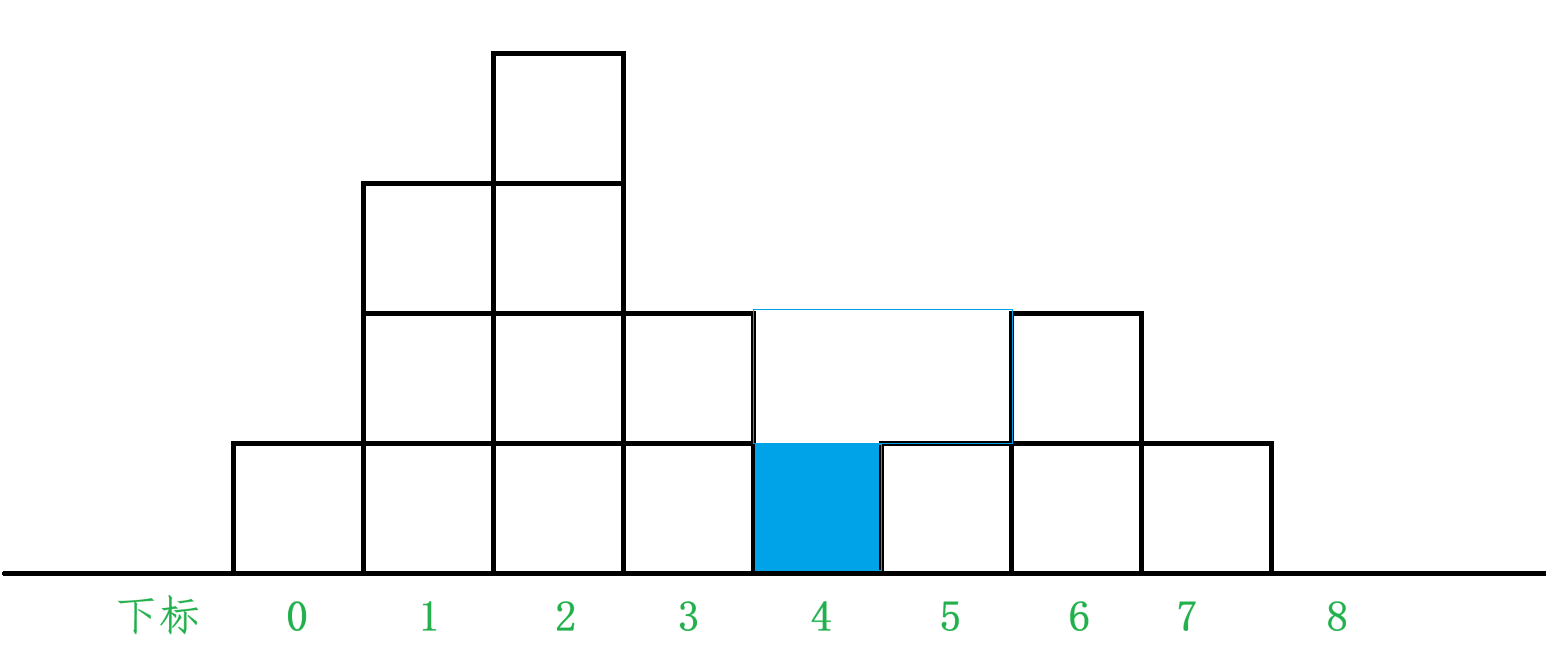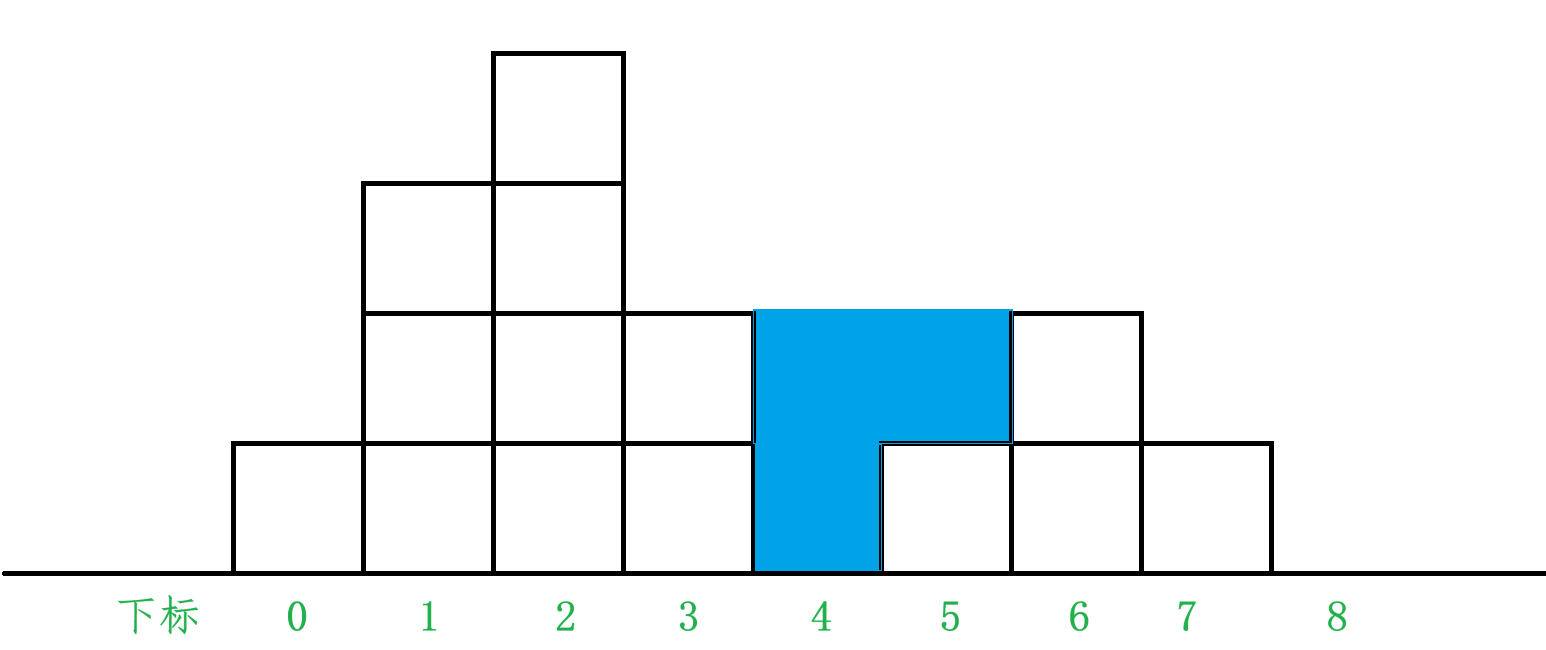
我们来看 4 下标的这个柱子是如何存水的,因为 4 下标的高度为 0,所以首先会先存一格水,然后由于它的右边有一个柱子高度为2, 3 号柱子的高度也为2,所以其能够再存储一格水,所以其存水量就是2,然后继续下雨,由于其右边柱子的最高高度为2,所以存的水会从右边流出去,所以其存水量就是2格。我们再来看 3 号柱子的存水量为什么是0,当 3 号柱子开始存水的时候,由于其左边柱子高度为 4,右边所有柱子的最高高度为2,所以当 4 与 5 号柱子存水量满了之后,其存的水会从右边流出去,所以其存水量就是 0。所以通过对这两个柱子存水量的分析,我们可以发现,其实 i 号柱子的存水量,是跟其左边所有柱子与右边所有柱子中的最高高度相关的(包括自己)。假设 leftmax 为其左边所有柱子的最大高度,rightmax 为其右边所有柱子的最大高度,i 号柱子的存水量 = min(leftmax, rightmax) - height[i]。
有了上述理论之后,我们就可以开始分析这道题目的解决办法了。首先我们先创建一个 leftmax 变量与 rightmax 变量用来记录第 i 号柱子左边与右边所有柱子的最大高度,所以这道题目的解题关键就是如何求出 leftmax 与 rightmax。我们假设有两个变量 left 和 right ,我们始终让其指向左边和右边中较高的那个柱子,起初我们假设最左边的柱子和最右边的柱子就是左边和右边的最高柱子,也就是 left = 0, right = height.size() - 1;此时 leftmax = height[0], rightmax = height[height.size() - 1],那么为了求出每一根柱子的存水量,我们可以进行如下操作:
(1) 如果 height[left] < height[right],说明 leftmax < rightmax,因为在遍历过程中,我们会让 left 和 right 中较小的那一个先向中间移动,所以移动到 height[left] 位置时,说明其前面的柱子高度是比 height[right] 小的,即leftmax < height[right] <= rightmax,所以此时只要 sum += (leftmax - height[left]),再 ++left 就可以了(sum 为接雨水的总量)。
(2) 同理,如果 height[left] >= height[right],那么只需要 sum += (rightmax - height[right]),--right 就可以了
(3) 在 left 和 right 移动过程中,更新 leftmax 和 rightmax
代码:
class Solution
{
public:
int trap(vector& height)
{
int sum = 0;
int left = 0, right = height.size() - 1;
int leftmax = 0, rightmax = 0;
while (left < right)
{
leftmax = max(height[left], leftmax);
rightmax = max(height[right], rightmax);
if (height[left] < height[right])
{
sum += leftmax - height[left];
++left;
}
else
{
sum += rightmax - height[right];
--right;
}
}
return sum;
}
}; 2 字符串的排列
题目描述:
给你两个字符串
s1和s2,写一个函数来判断s2是否包含s1的 排列。如果是,返回true;否则,返回false。换句话说,
s1的排列之一是s2的 子串 。示例 1:
输入:s1 = "ab" s2 = "eidbaooo" 输出:true 解释:s2 包含 s1 的排列之一 ("ba").示例 2:
输入:s1= "ab" s2 = "eidboaoo" 输出:false提示:
1 <= s1.length, s2.length <= 104s1和s2仅包含小写字母
题目解析:
这道题目题意很简单,题目会给我们两个字符串 s1 与 s2,判断 s2 中是否有 s1 字符串的排列,如果有,返回 true,没有返回 false。其中 s1 字符串中所有字符以任意顺序构成的字符串,就成为 s1 字符串的排列。比如 s1 = "abc","abc"、"acb"、"bac"、"bca"、"cab"、"cba" 都是 s1 字符串的排列。
算法讲解:
这道题目与之前的找到字符串中所有字母以为词很像,这道题目就是其变形,所以这道题目的解法就是:哈希表 + 滑动窗口。
(1) 首先利用 hash1 整数数组统计出 s1 字符串中字符出现的次数。之后定义 left = 0, right = 0, int hash2[128] = { 0 },count = 0,count 统计有效字符出现的次数
(2) 进窗口:hash2[s2[right]]++,++right,如果 hash1[s2[right]] >= hash1[s2[right]],++count
(3) 判断:如果 right - left + 1 > s1.size(),那就出窗口:if (hash1[s2[left]] >= hash2[s2[left]]),--count,hash2[s2[left]]--,++left
(4) 更新结果:由于判断是不满足条件时出窗口,所以我们在判断后进行更新结果,如果 count == s1.size(),代表 s2 中有效字符个数等于 s1 字符个数,那就返回 true
代码:
class Solution
{
public:
bool checkInclusion(string s1, string s2)
{
//用一个 hash 表来记录 s1 中字符出现次数
int hash1[128] = { 0 };
for (auto& ch : s1) hash1[ch]++;
//用 hash2 来记录 s2 中字符出现次数
int hash2[128] = { 0 };
int left = 0, right = 0, count = 0;
while (right < s2.size())
{
//进窗口
hash2[s2[right]]++;
if (hash1[s2[right]] >= hash2[s2[right]]) ++count;
//判断
while (right - left + 1 > s1.size())
{
//出窗口
if (hash1[s2[left]] >= hash2[s2[left]]) --count;
hash2[s2[left]]--;
++left;
}
//更新结果
if (count == s1.size()) return true;
++right;
}
return false;
}
};

 浙公网安备 33010602011771号
浙公网安备 33010602011771号