完整教程:模拟实现并查集

目录
并查集
概念
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集。
并查集(Union-Find)是一种树型的数据结构,用于处理一些不交集的合并及查询问题。它主要用于处理一些动态连通性问题。比如,在社交网络中判断两个人是否属于同一个社交网络群,或者在图论中判断两个顶点是否连通等。
举例
比如:某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体,数组中的数字代表:该小集体中具有成员的个数。【其中负号表示对应下标的人是“队长”,负数的绝对值代表该队伍有多少个人】

毕业后,学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,于是:
西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}就相互认识了,10个人形成了三个小团体。假设右三个群主0,1,2担任队长,负责大家的出行。
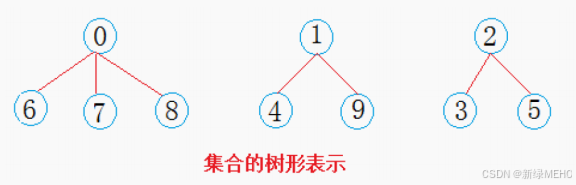
一趟火车之旅后,每个小分队成员就互相熟悉,称为了一个朋友圈。
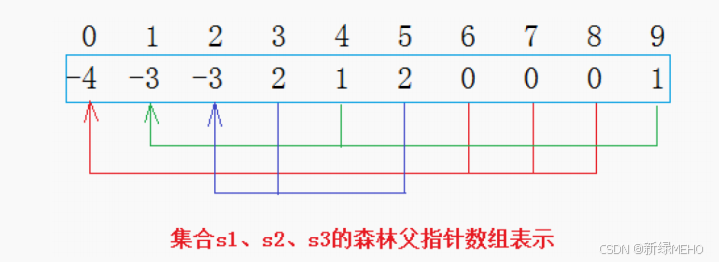
从上图可以看出:编号6,7,8同学属于0号小分队,该小分队中有4人(包含队长0);编号为4和9的同学属于1号小分队,该小分队有3人(包含队长1),编号为3和5的同学属于2号小分队,该小分队有3个人(包含队长1)。
仔细观察数组中内融化,可以得出以下结论:
1. 数组的下标对应集合中元素的编号
2. 数组中如果为负数,负号代表根,数字代表该集合中元素个数
3. 数组中如果为非负数,代表该元素双亲在数组中的下标
在公司工作一段时间后,西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起,两个小圈子的学生相互介绍,最后成为了一个小圈子:
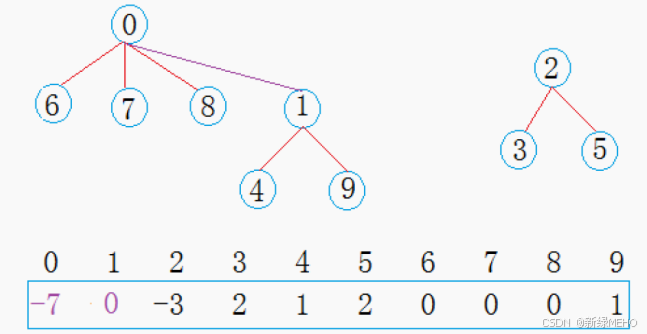
现在0集合有7个人,2集合有3个人,总共两个朋友圈。
通过以上例子可知,并查集一般可以解决一下问题:
1. 查找元素属于哪个集合
沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3. 将两个集合归并成一个集合
将两个集合中的元素合并
将一个集合名称改成另一个集合的名称
4. 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
模拟实现
基本框架
public class UnionFindSet {
public int[] elem;
public UnionFindSet(int n) {
this.elem = new int[n];
Arrays.fill(elem,-1);
}
}寻找该节点的根节点
public int findRoot(int x) {
if(x < 0) {
throw new IndexOutOfBoundsException("下标不合法,是负数");
}
while (elem[x] >= 0 ) {
x = elem[x];//1 0
}
return x;
}判断两个元素是否在同一集合中
public boolean isSameUnionFindSet(int x1,int x2) {
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2) {
return true;
}
return false;
}将不同集合里的两个元素合并到同一个集合
步骤:
1.首先找到两个不同元素的根节点
2.判断两个不同元素的根节点是否是同一个节点
3.如果是同一个节点,则返回,不进行合并
4.如果不是同一个节点,则将其中一个节点合并到另一个节点上
5.合并对应的操作是:将一个节点的值改为两个节点的值相加,被合并到另一个元素上的值为另一元素的下标
public void union(int x1,int x2) {
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2) {
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}统计并查集元素的数量
public int getCount() {
int count = 0;
for (int x : elem) {
if(x < 0) {
count++;
}
}
return count;
}打印整个并查集元素的值
public void print() {
for (int x : elem) {
System.out.print(x+" ");
}
System.out.println();
}完整代码
import java.util.Arrays;
public class UnionFindSet {
public int[] elem;
public UnionFindSet(int n) {
this.elem = new int[n];
Arrays.fill(elem,-1);
}
public int findRoot(int x) {
if(x < 0) {
throw new IndexOutOfBoundsException("下标不合法,是负数");
}
while (elem[x] >= 0 ) {
x = elem[x];//1 0
}
return x;
}
public boolean isSameUnionFindSet(int x1,int x2) {
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2) {
return true;
}
return false;
}
public void union(int x1,int x2) {
int index1 = findRoot(x1);
int index2 = findRoot(x2);
if(index1 == index2) {
return;
}
elem[index1] = elem[index1] + elem[index2];
elem[index2] = index1;
}
public int getCount() {
int count = 0;
for (int x : elem) {
if(x < 0) {
count++;
}
}
return count;
}
public void print() {
for (int x : elem) {
System.out.print(x+" ");
}
System.out.println();
}
}代码测试
public static void main(String[] args) {
UnionFindSet unionFindSet = new UnionFindSet(10);
System.out.println("合并:0和6:");
unionFindSet.union(0,6);
System.out.println("合并:0和7:");
unionFindSet.union(0,7);
System.out.println("合并:0和8:");
unionFindSet.union(0,8);
System.out.println("合并:1和4:");
unionFindSet.union(1,4);
System.out.println("合并:1和9:");
unionFindSet.union(1,9);
System.out.println("合并:2和3:");
unionFindSet.union(2,3);
System.out.println("合并:2和5:");
unionFindSet.union(2,5);
unionFindSet.print();
System.out.println("合并:8和1:");
unionFindSet.union(8,1);
unionFindSet.print();
System.out.println("查找是不是同一个集合");
System.out.println(unionFindSet.isSameUnionFindSet(6, 9));
System.out.println(unionFindSet.isSameUnionFindSet(8, 2));
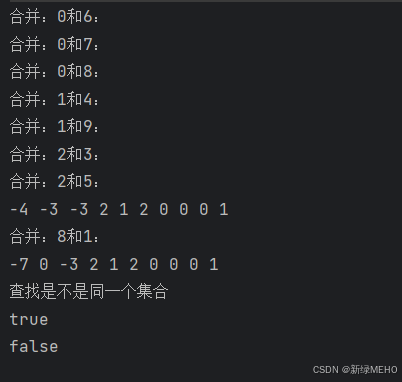
}运行结果:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号