少女折寿中

Luogu P4013 数字梯形问题

说实话这道题挺乐的，去年11月学网络流时碰到这道题，一直没想通，结果碰到考试月，被遣返回家，一个多月没摸了，今天看到这道题一下子想通了，于是想记下来。

题目传送门

P4013 数字梯形问题

题意

给定一个由 n 行数字组成的数字梯形如下图所示。

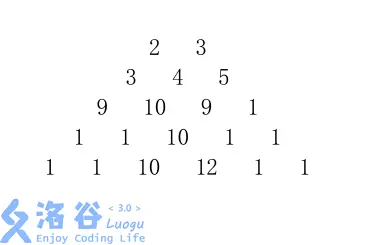
image

梯形的第一行有 m 个数字。从梯形的顶部的 m 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。

分别遵守以下规则：

  1. 从梯形的顶至底的 m 条路径互不相交；
  2. 从梯形的顶至底的 m 条路径仅在数字结点处相交；
  3. 从梯形的顶至底的 m 条路径允许在数字结点相交或边相交。

将按照规则 1，规则 2，和规则 3 计算出的最大数字总和并输出，每行一个最大总和。

思路

很显然，这道题的思路是最大费用最大流。但三个规则中，我认为2、3是比较简单的，而规则1建图略微复杂一点。我们先从规则3讲起。

规则3

从梯形的顶至底的 m 条路径允许在数字结点相交或边相交，也可以说是没有任何限制了。

我们按以下思路建图：

  1. 源点到第一行各点建容量为1，费用为0的边；
  2. 除最后一行的每一个点向下一行左下、右下两个点分别建容量为INF，费用为负的该点数字的边；
  3. 最后一行的每一个点向汇点建容量为INF，费用为为负的该点数字的边。

按样例建图如下图所示。

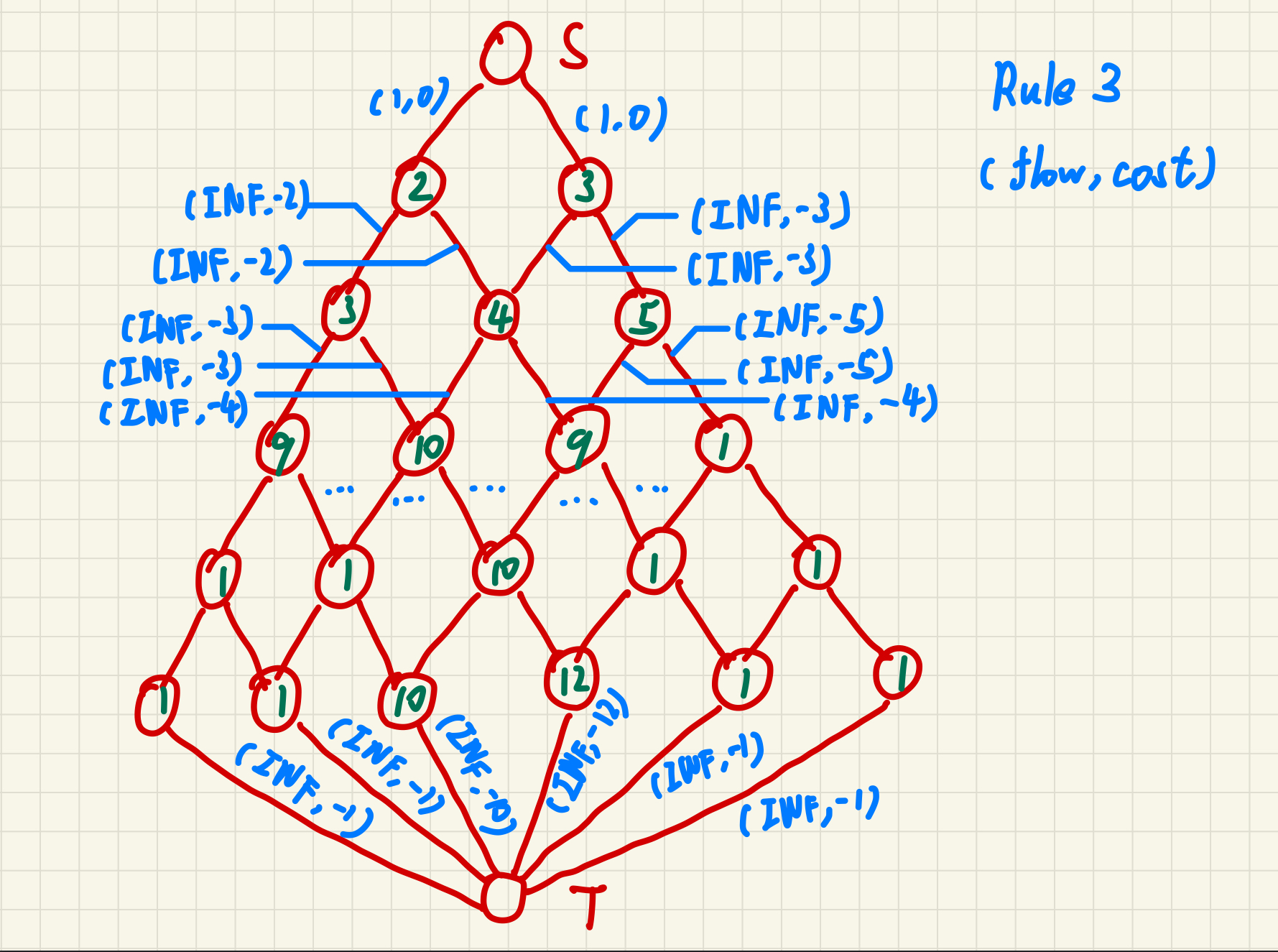
image

图中S为源点，T为汇点。

按上述建边方法，源点向第一行两个点分别建边（1，0）；第一行第一个点向第二行第一、二个点分别建边（INF，-2）；第一行第二个点分别向第二行第二、三个点分别建边（INF，-3）……；最后一行各点向汇点建边（INF，-该点数字）。建完边后跑费用流，负的费用即为答案。

规则2

从梯形的顶至底的 m 条路径仅在数字结点处相交，相比第3条规则，路径两两不能共用一条边，即每条边允许容量为1。

稍微改一下规则3，我们就可以得到下面建图方法：

  1. 源点到第一行各点建容量为1，费用为0的边；
  2. 除最后一行的每一个点向下一行左下、右下两个点分别建容量为1，费用为负的该点数字的边；
  3. 最后一行的每一个点向汇点建容量为INF，费用为为负的该点数字的边。注意这里建边容量为INF，因为最底层向汇点不用限制流量。

按样例建图如下图所示。

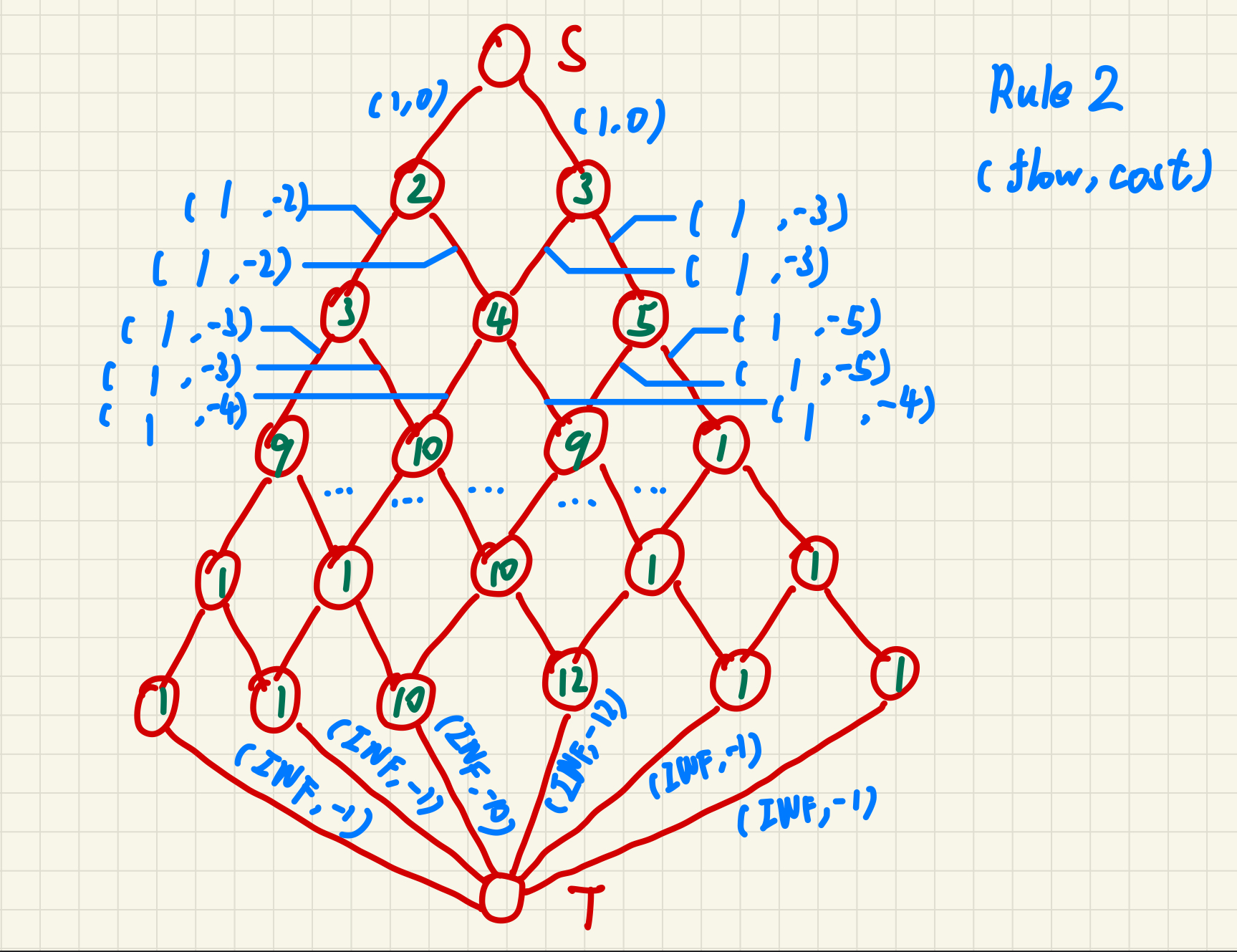
image

按此方法建图即可保证这些路径不会在边处重合。建图完后依旧跑费用流取负费用即为答案。

规则1

从梯形的顶至底的 m 条路径互不相交，相较于第2条规则，各路径也不能在点处相交，这意味着我们需要在规则2的基础上，对点限流。

对点限流的方法即为拆点，将一个点拆为两个点，分别为“入点”和“出点”，所有连向该点的边都应连向该点的入点，该点的所有出边都应从出点连出；每个点的入点还需要向该点的出点连一条容量为1，费用为0的边，即可限制每一点的流量。

我们可以得到如下建图方法：

  1. 源点到第一行各点的入点建容量为1，费用为0的边；
  2. 除最后一行的每一个点的出点向下一行左下、右下两个点的入点分别建容量为1，费用为负的该点数字的边；
  3. 最后一行的每一个点的出点向汇点建容量为INF，费用为为负的该点数字的边。注意这里建边容量为INF，因为最底层向汇点不用限制流量；
  4. 每个点的入点向出点建一条容量为1，费用为0的边。

代码

规则3

void ans3() {
    cnt = 0;//初始化图
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            if (i == 1)add(S, get(i, j, 0), 1, 0);//源点到第一行各点建容量为1，费用为0的边
            if (i == n)add(get(i, j, 0), T, INF, -num[i][j]);//最后一行的每一个点向汇点建容量为INF，费用为为负的该点数字的边
            else {
                //除最后一行的每一个点向下一行左下、右下两个点分别建容量为INF，费用为负的该点数字的边
                add(get(i, j, 0), get(i + 1, j, 0), INF, -num[i][j]);
                add(get(i, j, 0), get(i + 1, j + 1, 0), INF, -num[i][j]);
            }
        }
    }
    int flow, cost;
    EK(flow, cost);//跑EK费用流
    cout << -cost << endl;//输出负费用
}

规则2

void ans2() {
    cnt = 0;//初始化图
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            if (i == 1)add(S, get(i, j, 0), 1, 0);//源点到第一行各点建容量为1，费用为0的边
            if (i == n)add(get(i, j, 0), T, INF, -num[i][j]);//最后一行的每一个点向汇点建容量为INF，费用为为负的该点数字的边。注意这里建边容量为INF，因为最底层向汇点不用限制流量
            else {
                //除最后一行的每一个点向下一行左下、右下两个点分别建容量为1，费用为负的该点数字的边
                add(get(i, j, 0), get(i + 1, j, 0), 1, -num[i][j]);
                add(get(i, j, 0), get(i + 1, j + 1, 0), 1, -num[i][j]);
            }
        }
    }
    int flow, cost;
    EK(flow, cost);//跑EK费用流
    cout << -cost << endl;//输出负费用
}

规则1

void ans1() {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            if (i == 1)add(S, get(i, j, 0), 1, 0);//源点到第一行各点的**入点**建容量为1，费用为0的边
            if (i == n)add(get(i, j, 1), T, 1, -num[i][j]);//最后一行的每一个点的**出点**向汇点建容量为INF，费用为为负的该点数字的边。注意这里建边容量为INF，因为最底层向汇点不用限制流量
            else {
                //除最后一行的每一个点的**出点**向下一行左下、右下两个点的**入点**分别建容量为1，费用为负的该点数字的边
                add(get(i, j, 1), get(i + 1, j, 0), 1, -num[i][j]);
                add(get(i, j, 1), get(i + 1, j + 1, 0), 1, -num[i][j]);
            }
            //每个点的**入点**向**出点**建一条容量为1，费用为0的边
            add(get(i, j, 0), get(i, j, 1), 1, 0);
        }
    }

    int flow, cost;
    EK(flow, cost);//跑EK费用流
    cout << -cost << endl;//输出负费用
}

完整代码

点击查看代码 
/*
 * ycccc319
 */
#include <bits/stdc++.h>

using namespace std;
const int N = 2010, M = 100100, INF = 0x3f3f3f3f;

class node {
public:
    int v, f, w, next;
} edge[M];

int n, m, S, T;
int cnt = 0, head[N];
int d[N], pre[N], q[N], incf[N];
bool vis[N];

void add(int u, int v, int c, int w) {
    edge[cnt].v = v, edge[cnt].f = c, edge[cnt].w = w, edge[cnt].next = head[u], head[u] = cnt++;
    edge[cnt].v = u, edge[cnt].f = 0, edge[cnt].w = -w, edge[cnt].next = head[v], head[v] = cnt++;
}

bool spfa() {
    int hh = 0, tt = 1;
    memset(d, INF, sizeof d);
    memset(incf, 0, sizeof incf);
    q[0] = S, d[S] = 0, incf[S] = INF;
    while (hh != tt) {
        int now = q[hh++];
        if (hh == N)hh = 0;
        vis[now] = 0;
        for (int i = head[now]; ~i; i = edge[i].next) {
            int to = edge[i].v;
            if (edge[i].f && d[to] > d[now] + edge[i].w) {
                d[to] = d[now] + edge[i].w;
                pre[to] = i;
                incf[to] = min(edge[i].f, incf[now]);
                if (!vis[to]) {
                    q[tt++] = to;
                    if (tt == N)tt = 0;
                    vis[to] = 1;
                }
            }
        }
    }
    return incf[T] > 0;
}

void EK(int &flow, int &cost) {
    flow = cost = 0;
    while (spfa()) {
        int t = incf[T];
        flow += t, cost += t * d[T];
        for (int i = T; i != S; i = edge[pre[i] ^ 1].v) {
            edge[pre[i]].f -= t;
            edge[pre[i] ^ 1].f += t;
        }
    }
    return;
}

int num[22][42];

int get(int x, int y, int c) {//在规则1中，c为1时是出点，为0时是入点，规则2、3里不适用
    return x * 40 + y + c * 1000;//这里为了省事直接对出点+1000了
}

void ans1() {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            if (i == 1)add(S, get(i, j, 0), 1, 0);//源点到第一行各点的**入点**建容量为1，费用为0的边
            if (i == n)
                add(get(i, j, 1), T, 1,
                    -num[i][j]);//最后一行的每一个点的**出点**向汇点建容量为INF，费用为为负的该点数字的边。注意这里建边容量为INF，因为最底层向汇点不用限制流量
            else {
                //除最后一行的每一个点的**出点**向下一行左下、右下两个点的**入点**分别建容量为1，费用为负的该点数字的边
                add(get(i, j, 1), get(i + 1, j, 0), 1, -num[i][j]);
                add(get(i, j, 1), get(i + 1, j + 1, 0), 1, -num[i][j]);
            }
            //每个点的**入点**向**出点**建一条容量为1，费用为0的边
            add(get(i, j, 0), get(i, j, 1), 1, 0);
        }
    }

    int flow, cost;
    EK(flow, cost);//跑EK费用流
    cout << -cost << endl;//输出负费用
}

void ans2() {
    cnt = 0;//初始化图
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            if (i == 1)add(S, get(i, j, 0), 1, 0);//源点到第一行各点建容量为1，费用为0的边
            if (i == n)
                add(get(i, j, 0), T, INF, -num[i][j]);//最后一行的每一个点向汇点建容量为INF，费用为为负的该点数字的边。注意这里建边容量为INF，因为最底层向汇点不用限制流量
            else {
                //除最后一行的每一个点向下一行左下、右下两个点分别建容量为1，费用为负的该点数字的边
                add(get(i, j, 0), get(i + 1, j, 0), 1, -num[i][j]);
                add(get(i, j, 0), get(i + 1, j + 1, 0), 1, -num[i][j]);
            }
        }
    }
    int flow, cost;
    EK(flow, cost);//跑EK费用流
    cout << -cost << endl;//输出负费用
}

void ans3() {
    cnt = 0;//初始化图
    memset(head, -1, sizeof(head));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            if (i == 1)add(S, get(i, j, 0), 1, 0);//源点到第一行各点建容量为1，费用为0的边
            if (i == n)add(get(i, j, 0), T, INF, -num[i][j]);//最后一行的每一个点向汇点建容量为INF，费用为为负的该点数字的边
            else {
                //除最后一行的每一个点向下一行左下、右下两个点分别建容量为INF，费用为负的该点数字的边
                add(get(i, j, 0), get(i + 1, j, 0), INF, -num[i][j]);
                add(get(i, j, 0), get(i + 1, j + 1, 0), INF, -num[i][j]);
            }
        }
    }
    int flow, cost;
    EK(flow, cost);//跑EK费用流
    cout << -cost << endl;//输出负费用
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> m >> n;
    S = 0, T = 1;
    memset(head, -1, sizeof head);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < m + i; j++) {
            cin >> num[i][j];
        }
    }
    ans1();
    ans2();
    ans3();
    return 0;
}
posted @ 2023-01-15 10:13  ycccc319  阅读(36)  评论(1)    收藏  举报