斜率优化

斜率优化

前置芝士：\(斜率 = \frac{a_y-b_y}{a_x-b_x}\)

列题：P3195 [HNOI2008] 玩具装箱

首先你要知道这是 \(dp\)。

其次你要写出暴力来，这里简略一下，设 \(q_i\) 为前缀和：\(f_i = min(f_j + (q_i - q_j + i - j - 1 - l)^2)\)。
正片开始：

首先，我们发现 \(dp\) 式太复杂了，所以化简一下，因为 \(i\) 和 \(l\) 属于暂时常数，所以将其分离出来，可设 \(x_i=q_i+i,r_i=x_i-l-1\)，则

\(原式 = f_j+(r_i-x_j)^2\)，

将括号分解：

\(= f_j+{r_i}^2+{x_j}^2-2r_ix_j\)

再将 \(i\) 分离（单单与 \(i\) 有关的，这里消掉了，但是最终要加上！）：

\(f_j+{x_j}^2-2r_ix_j\)

这里出来了单独式和系数式，可以在将两种分离开来，设 \(y_i=f_i+{x_i}^2\)：

\(y_j-2r_ix_j\)

这里化不下去了，所以可设两个决策点 \(a, b\)，设 \(a\) 比 \(b\) 更优，有：

\(y_a-2r_ix_a < y_b-2r_ix_b\)

\(y_a-y_b < 2r_i(x_b-x_a)\)

\(y_a-y_b > 2r_i(x_a-y_b)\)

因为我们并不关心 \(x_a\) 和 \(y_b\) 之间的关系，所以不管了：

\(\frac{y_a-y_b}{x_a-x_b} > 2r_i\)

此时我们发现，\(\frac{y_a-y_b}{x_a-x_b}\) 是个斜率式，所以可以建系，此时有：如果斜率大于 \(2r_i\)，则 \(a\) 的比 \(b\) 的更优。

考虑如何用斜率来优化，很明显，当我们把一个个点维护出来后，会有一个由斜率连成的线，此时会有凸壳：

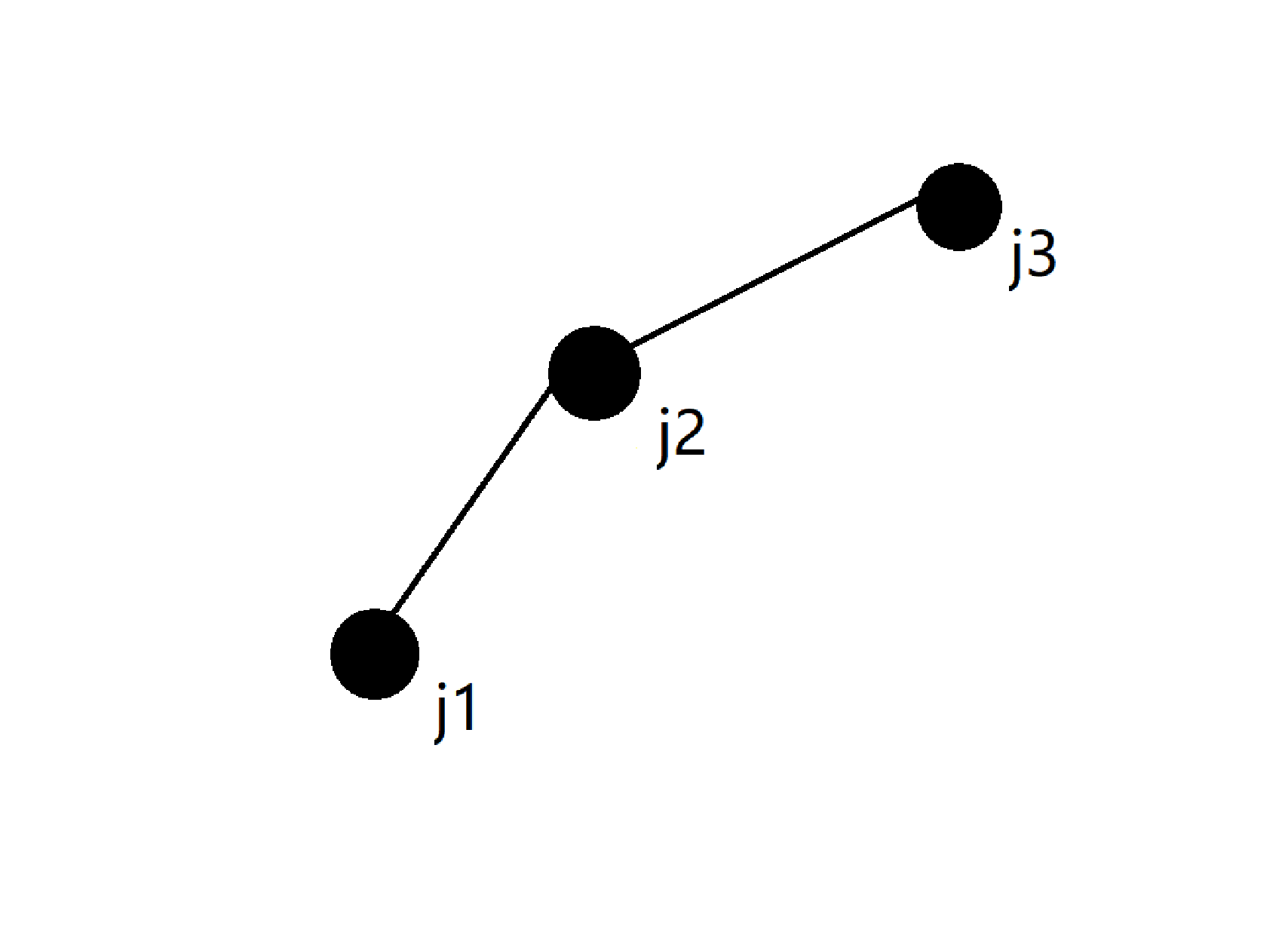
通过此图，我们可以得知：此时 \(j2\) 永远也不可能是最优的，因为如果 \(j2\) 是最优的，那么 \(2r_i\) 必然是小于 \(j2\) 和 \(j3\) 的斜率，那么 \(2r_i\) 就会小于 \(j1\) 到 \(j2\) 的斜率（一个上凸，斜率自然大一些），所以 \(j1\) 比 \(j2\) 优，所以 \(j2\) 永远不是最优的。那么对于这些完全不可能是最优的点，我们就没有必要在维护了，那么我们可以用个栈维护，因为新加的点只会对最近的几个点有影响，所以用栈即可满足。

可是维护了这样一个凸壳有什么用呢？

当我们考虑到了 \(i\)，就必然有一个 \(2r_i\)（似乎是废话），先说结论：用斜率为 \(2r_i\) 的直线去切我们维护的凸壳，第一个切到的点，就是最优决策点。

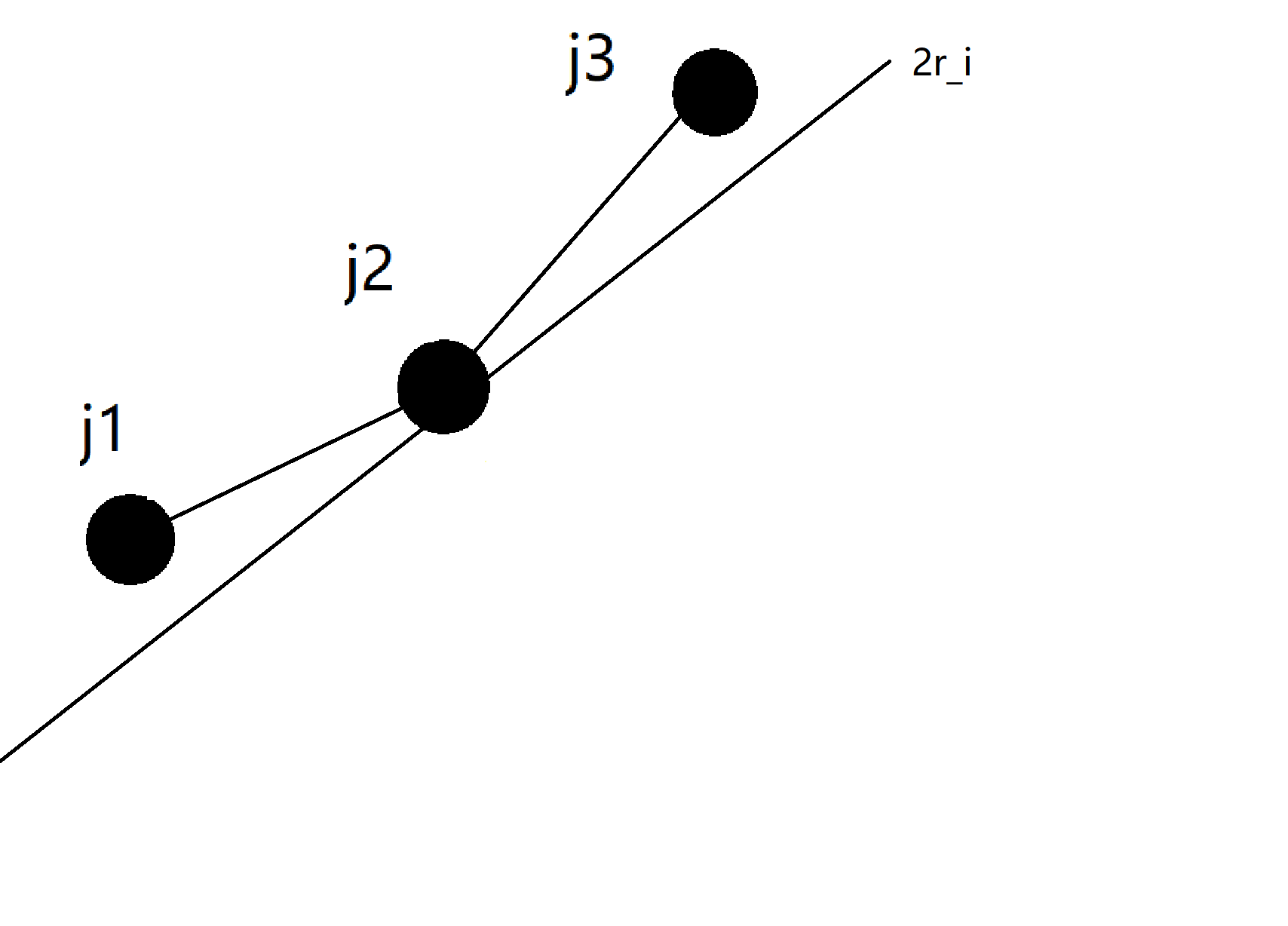
为什么是这样呢？（以上为图示，可以结合食用）我们可以思考这个点（待会被称为当前点），在它往前走（也就是上面的那个）的点的斜率比 \(2r_i\) 大，所以当前点是优的，在它往后走（也就是下面的那个）的点的斜率比 \(2r_i\) 小，所以当前点更优，所以是最优决策点。

由图可知，其实切上去，就是找到第一个上面斜率大于 \(2r_i\) 的点，二分即可。

最后提醒一句，这道题很水，所以这么做就行了，因为我们的 \(x_i\) 永远在递增，可是像 [NOI2007] 货币兑换 这种不递增的，就得用 \(CDQ\) 了！

code

#include <algorithm>
#include <iostream>
#define int long long

using namespace std;

const int MaxN = 5e4 + 10;
const double eps = 1e-7;

int f[MaxN], s[MaxN], p[MaxN], y[MaxN], x[MaxN], o[MaxN], tot, n, l, len;

bool Check(int d, int e) {
  if (y[s[d + 1]] == -1e18 && x[s[d + 1]] == -1e18) {
    return 1;
  }
  return (y[s[d + 1]] - y[s[d]]) > e * (x[s[d + 1]] - x[s[d]]);
}

signed main() {
  cin >> n >> len;
  for (int i = 1; i <= n; i++) {
    cin >> p[i], p[i] += p[i - 1], x[i] = p[i] + i;
  }
  x[n + 1] = -1e18, y[n + 1] = -1e18;
  f[1] = (p[1] - len) * (p[1] - len), s[++tot] = 1, o[1] = x[1] - len - 1, y[1] = f[1] + x[1] * x[1];
  for (int i = 2; i <= n; i++) {
    int l = 1, r = tot;
    s[tot + 1] = n + 1;
    /*for (int j = 1; j <= tot; j++) {
      cout << s[j] << " ";
    }
    cout << endl;*/
    o[i] = x[i] - len - 1;
    while (l < r) {
      int mid = (l + r) >> 1;
      Check(mid, 2 * o[i]) ? r = mid : l = mid + 1;
    }
    l = s[l];
    f[i] = min(o[i] * o[i] + y[l] - 2 * o[i] * x[l], (p[i] + i - 1 - len) * (p[i] + i - 1 - len)), y[i] = f[i] + x[i] * x[i];
    //cout << T(y[1], y[2], x[1], x[2]) << " " << f[i] << " " << o[i] << " " << y[l] << " " << x[l] << ' ' << l << endl;
    while (tot > 1 && (y[s[tot]] - y[s[tot - 1]]) * (x[i] - x[s[tot]]) > (y[i] - y[s[tot]]) * (x[s[tot]] - x[s[tot - 1]])) {
      tot--;
    }
    s[++tot] = i;
  }
  cout << f[n] << endl;
  return 0;
}