MathBasic - 02 - (初级)代数方程&(初级)直角坐标系

前言

• 这是我学习美国数学课程-从小学到大学-中英cc字幕-数学英语课程的笔记，我的数学基础巨差，看这个刚合适，不太难又容易理解。

• 其中会添加一些我自己的理解和示例

• 本次核心内容（该课程的p23-p46讲）

  • 代数导论

    • 多项式基本
    • 多项式化简与运算
    • 一元二次方程基本形式与求解方法

  • 直角坐标系

    推荐好用的在线绘图工具：GeoGebra

    • 直线方程
    • 坐标系与一元二次方程组求解

  • 绝对值与数字分类

023 代数导论

算数运算与代数运算不同

运算对象不同

• 算术运算:常量
• 代数运算:变量

代数运算表达式

包含一个或多个变量&常量的运算式

• 示例：\(x + 5 = 0\)

如何列出代数运算表达式非常重要

024 代数的基本运算性质

• 加法以及乘法的结合律 交换律 分配律

  • 分配律以及逆分配律在代数运算中非常常见

  • 示例：

    \[分配律：3x(x+2) = 3x^2 + 6x\\ 逆分配律(找到两个代数表达式的最大公因子)\\ 5x^2 + 10x = 5x(x+2) \]

• 代数项减去0和代数项乘以1运算结果都为其本身:\(x - 0 = x\);\(x \times 1 = x\)

• 代数项加上负的代数项的和为0: \(x + (-x) = 0\)

• 任何代数项乘以它的倒数都为1:\(x \times \frac{1}{x} = 1(x\neq0)\)

025 代数方程及其解(简单一元一次方程求解)

方法

• 在方程两边执行撤回操作(将运算撤销)，直到只剩代数项

示例：

\[x + 5 = 0 \\x + 5 - 5 = 0 - 5 \\x = -5 \]

026 存在系数的一元一次方程求解

求解方法

1. 常数项处理后，再处理代数项
2. 消除代数项系数，求解

示例：\((5x-4)/3=2(x+2)\)

\[(5x-4)/3=2(x+2)\\ 5x-4 = 6(x+2)\\ 5x-4 = 6x+12\\ -16 = x \]

027 代数文字题 (现实应用题)

构建代数方程，求解方程

• 厘清题目之间的关系
• 设定恰当的未知数
• 利用关系构建方程、解决方程

028 代数不等式

形式

• 诸如 \(x<5\)
  • x的值可以是任何小于5的数字

代数不等式求解

• 求解范围：代数不等式的求解是一个范围，即解集(配合数轴能够更好理解)

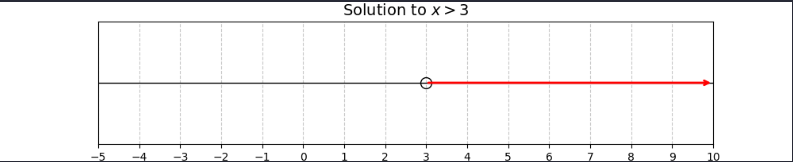
• 注意：未知数项为负数，在去除符号计算时关系运算符应该反转关系符号

  • \(-x>1 ==> x<1\)

029 平方根 立方根 其他根(代数方程)

一元二次方程

• 形式:\(x^2=4\)
• 解存在两个：\(\sqrt{4}=\pm2\)​

完全平方根、算数平方根 、奇偶次跟解的数量与无理数根

• 算数平方根： 一元二次方程 正值解

• 完全平方根：4 9 16 25 36 49 64 81 100 121 ...

• 无理数根(不能被分数表示)：$\sqrt{2} $

• 奇偶次根的解的数量

  • 偶数次根：两个解
  • 奇数次根：一个解

根与分数指数幂的相互转化

口诀：上下对内外

\(x^\frac{a}{b} = \sqrt[b]{x^a}\)

030 表达式简化 （分数以及指数、根）

应用分数、指数和根式的运算规则

示例：\(\frac{(x^\frac{1}{3}·x^\frac{2}{3})^2}{x^\frac{3}{2}}\)​

\[\frac{(x^\frac{1}{3}·x^\frac{2}{3})^2}{x^\frac{3}{2}}\\ =\frac{x^2}{x^\frac{3}{2}}\\ =x^\frac{1}{2} \]

031 使用根和指数求解代数方程

有根式与未知数方程的简单求解，依旧应用指数运算规则即可

示例：\(\sqrt[3]{x^3+9}=6\)

\[\sqrt{x^3+9}=6\\x^3+9 = 36\\x^3=27\\x=3 \]

032 多项式介绍 - (一元多项式)

多项式的基本形式

\(\boxed{a_0 + a_1X + ...+a_{n-1}X^{n-1} + a_nX^n}\)

• 多项式的项数

• 多项式的未知数的最高次幂称为该多项式的次数:也被称为*次多项式。

  • 如：\(5x^2 -2x + 7\);这被称为2次多项式

• 复杂多项式的求解是非常具有难度的

示例

• 单项式：\(2x\)
• 二项式：\(2x^2 + 1\)
• 三项式：\(2x^2 + x + 1\)
• 多项式：\(3x^3+2x^2 + x + 1\)

033 多项式化简1：多项式间的加减法

• 运算规则与之前整数间运算相同，可采用竖式运算的方式（合并同幂项&常数项）

• 示例：\((x^3 + 6x - 1) - (-5x^2 -x + 8)\)​

  \[(x^3 + 6x - 1) + 5x^2 + x - 8)\\ =x^3 + 5x^2 + 7x -9 \]

034 多项式化简2：多项式与多项式相乘

• 采用乘法的分配律即可(FOIL方法)

  • FOIL：即第一个多项式的首项依次乘以第二个多项式的每一项直至尾项，之后第一个多项式的第二项依次乘以第二个多项式的每一项直至尾项，如此循环直至第一个多项式结束，此后化简即可

• 示例：\((2x-9)(3x+5)\)

  \[(2x-9)(3x+5)\\=6x^2+10x-27x-45\\=6x^2-17x-45 \]

035 方程求解1：通过因式分解求解一元二次方程

一元二次方程的标准形式

• \(\boxed{ax^2 + bx+c=0(a\neq0)}\)

因式分解

上高中前的第一课！“因式分解”大梳理,这个非常容易听明白

• \(\boxed{Ax^2 + Bx +c = (ax+b)(cx+d)}\)

定义：把一个多项式化成几个整式的乘积的形式（把和转换成积的形式）

其中的重要的方法 - 十字相乘法：十字相乘（首尾化积，十字相乘，求和凑中，横向书写）

如何判断一个二次多项式是否能够因式分解

• 假想一个二次多项式的结果为0，,之后利用接下来学习的求根公式来判断是否有解，如有解，那么其中一个因式分解子项为\((x-根)\)。

例题

• \[6x^2+7x-3=0\\因式分解可得：(2x+3)(3x-1) \]

• \[x^2-2y^2+xy+x+5y-2=0 \]
  \[首先观察能不能将多项式转化成关于x或者关于y的2次多项式\\ x^2+xy+x-2y^2+5y-2 = 0\\ \boxed{x^2}+\boxed{(y+1)x}-\boxed{(2y^2-5y+2)}=0\\ x^2+(y+1)x-(2y-1)(y-2)=0\\ x^2+(y+1)x+(2y-1)(2-y)=0\\ (x+2y-1)(x+2-y)=0 \]

特殊的一元二次方程

满足：\(a+b+c=0\)的一元二次方程，其因式分解为\((x-1)(ax-c)=0\)

036 方程求解2： 凑完全平方(配平方法)求解一元二次方程

1.配平方法

需要将方程转化为一个完全平方形式(是下一节求根公式的应用)

​ \(\boxed{ax^2 + bx+c=0(a\neq0)}\)

1. 将方程转化为标准形式：\(ax^2 + bx+c=0\)
2. 将二次项系数化为1：\(x^2 + \frac{b}{a}x+\frac{c}{a}=0\)
3. 凑完全平方
   • 将常数项移动到等号右侧：\(x^2 + \frac{b}{a}x=-\frac{c}{a}\)
   • 添加常数项来凑完全平方式：\((\frac{b}{a}\div2)^2 = \frac{b^2}{4a^2}\)
4. 将添加的常数项加到等式的左右两边
5. 将等式写成完全平方形式：\((x+\frac{b}{2a})^2= -\frac{c}{a}+\frac{b^2}{4a^2}\)
6. 最后合并等号右侧的常数项，两边同时开方即可得解

2.示例

\[4x^2+x-3=0\\ 移动常数项\\ 4x^2+x=3\\ 将2次项的系数化为1\\ x^2+\frac{x}{4}=\frac{3}{4}\\ 凑完全平方 - 找到常数项\\ x^2+\frac{x}{4}+\frac{1}{64}=\frac{3}{4}+\frac{1}{64}\\ 写成完全平方形式\\ (x+\frac{1}{8})^2 = \frac{49}{64}\\ 两边同时开平方\\ x + \frac{1}{8} = \pm\frac{7}{8}\\ 得解 x = \pm\frac{7}{8} - \frac{1}{8}\\ x_1 = \frac{3}{4},x_2 = -1 \]

037 方程求解3： 求根公式求解一元二次方程

1.求根公式(韦达定理)

\[\boxed{x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}} \]

2.求根公式推导过程 - 配平方法

\[ax^2+bx+c=0\\ x^2+\frac{b}{a}=-\frac{c}{a}\\ x^2+\frac{b}{a}+(\frac{b}{2a})^2 = -\frac{c}{a}+(\frac{b}{2a})^2\\ (x+\frac{b}{2a})^2=-\frac{c}{a}+\frac{b^2}{4a^2}=\frac{b^2-4ac}{4a^2}\\ x+\frac{b}{2a}=\frac{\pm\sqrt{b^2-4ac}}{2a}\\ x = \frac{-b\pm\sqrt{b^2-4ac}}{2a} \]

3.示例

\(2x^2+5x-25=0\)

• 由求根公式可得：\(x_1=\frac{-b+\sqrt{b^2-4ac}}{2a}=\frac{5}{2};x_2=\frac{-b-\sqrt{b^2-4ac}}{2a}=-5\)

一元二次方程的特殊关系

一元二次方程根与系数的关系

\[x_1+x_2=-\frac{b}{a}\\ x_1x_2=\frac{c}{a} \]

一元二次方程根的判别式

\[\Delta = b^2-4ac\\ \begin{Bmatrix} \Delta>0方程有两个不相等的实数根\\ \Delta=0方程有两个相等的实数根\\ \Delta<0方程有两个复根 \end{Bmatrix} \]

038 高数知识：高次项方程求解综合除法(就离谱 - 这节可以跳过)

1.综合除法简介

• 定义：用来判断一个式子是否是一个多项式的因式 可以用来求解高次项方程

2.如何使用

• 假设一个式子是一个多项式的解,直接猜多项式的解

• 如何假设解(并非所有解，只是可能性)：\(\pm\)常数项因数组与最高次项的系数的因数组之比

  • \[\boxed2x^3 + 3x^2 -3x -\boxed2 = 0\\ \pm\frac{常数项因数组:1,2}{最高次项因数组:1,2} \]

• 代入解：

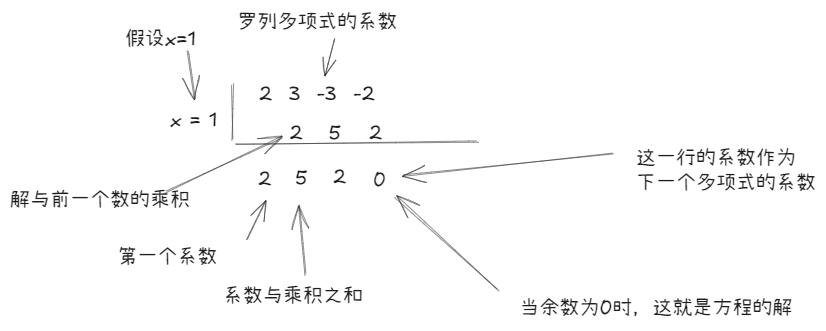  \[因为x=1是多项式的一个解\\ 因此原方程可以改写为: (x-1)(2x^2+5x+2)=0;\\ 后面是一个1元2次方程，可以利用因式分解或者求根公式来求解 \]

• 高次项降次之后方便计算。

3.示例

\[15x^4+x^3-52x^2+20x=16 \]

039 代数分式方程式化简 - 示例

为接下来绘制图做准备

\[\frac{1}{1-\sqrt{2}}=\frac{1\times(1+\sqrt{2})}{(1-\sqrt{2})\times(1+\sqrt{2})}=-1-\sqrt{2} \]

\[\frac{1+\frac{1}{x}}{1-\frac{1}{x}}=\frac{\frac{x+1}{x}}{\frac{x-1}{x}}=\frac{x+1}{x-1} \]

040 代数方程式和坐标系

有一个非常好用的工具：GeoGebra绘图

平面坐标系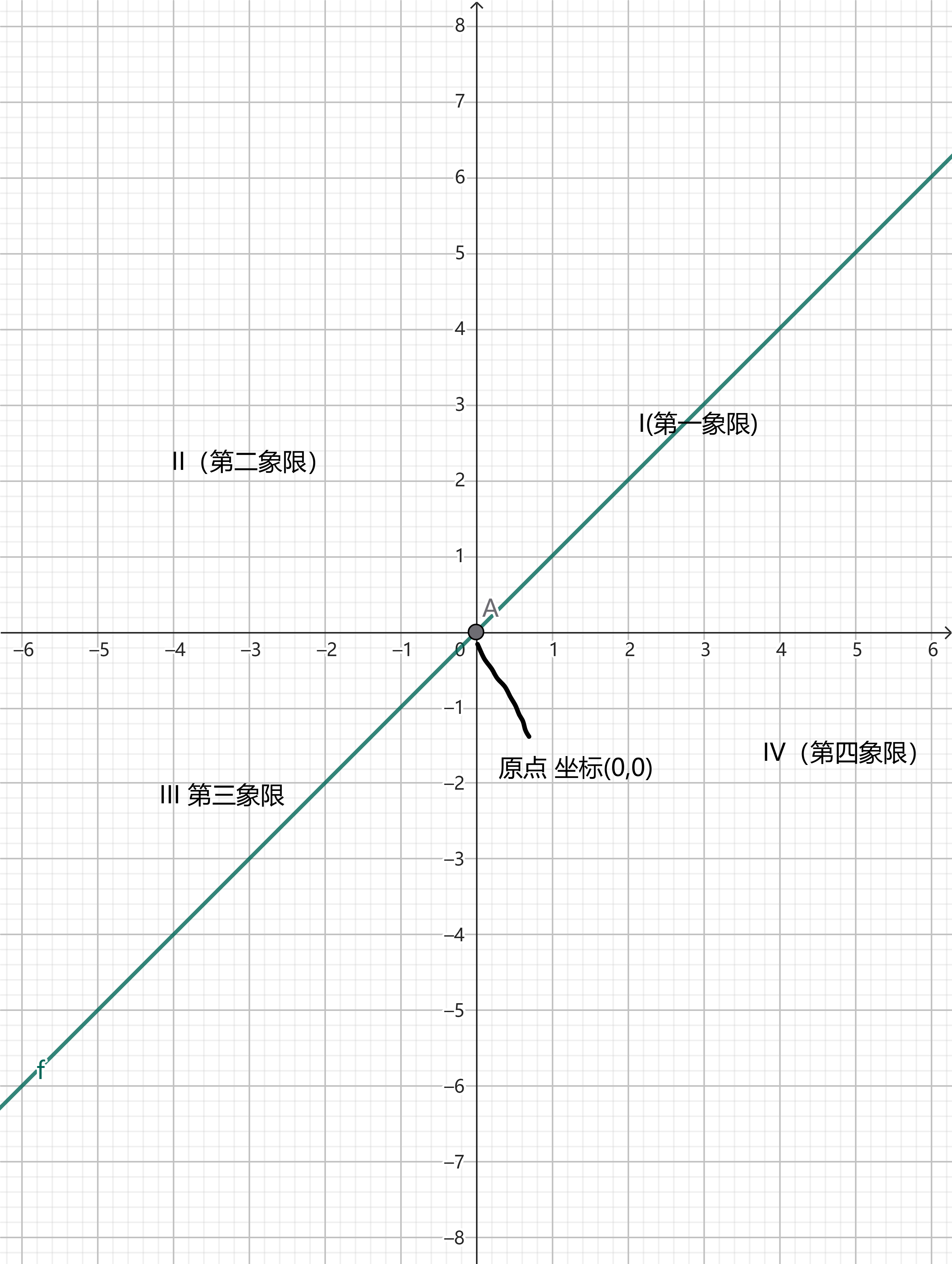

• 由横向的X轴和纵向的Y轴组成
• 象限：右上角开始依次逆时针为 第一至第四象限

图形是方程的可视化表示,方便展示两个变量间的关系

示例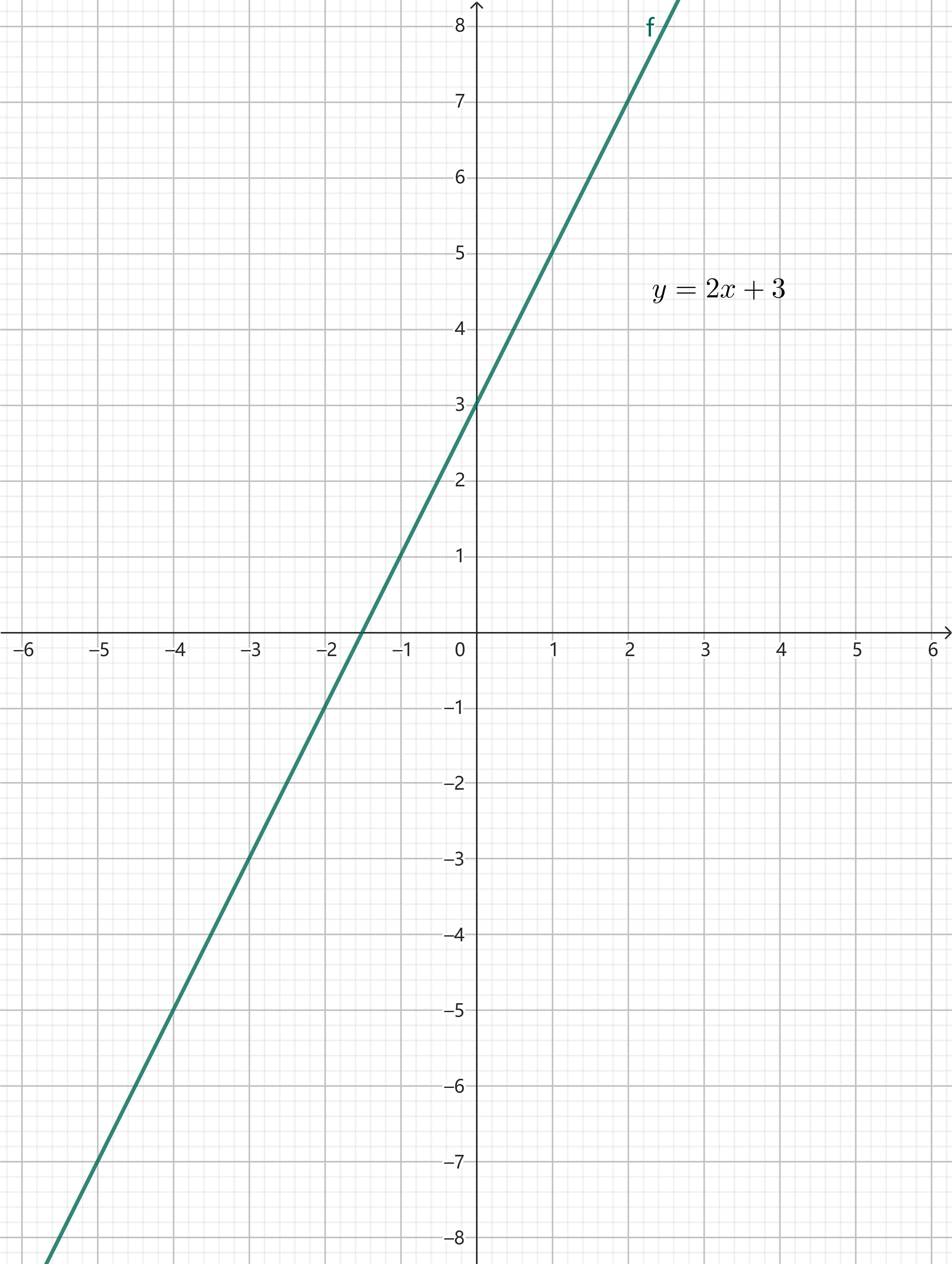

041 斜率截距方程 - 斜截式

斜率截距方程

对于直角坐标系，一次函数：\(y=mx+b\)，若m&均不等于0，则m是斜率，b是截距。

• m表示斜率；b表示截距(当x为零时，y的值,也就是该直线与y轴交点的纵坐标的值)

计算斜率

• 变化量计算

\[m = \frac{\Delta y}{\Delta x}(\Delta指变化量) \]

• 已知直角坐标系内两点的坐标\((x_1,y_1)和(x_2,y_2）\)
  \[m=\frac{y_2=y_1}{x_2-x_1} \]

斜率的特殊情况

• 与x轴平行时：斜率为0
• 与y轴平行时：斜率未定义
• y=x时；斜率为1
• 斜率的正负决定了线段的朝向
  • 正：朝向右侧
  • 负：朝向左侧

042 根据已知条件求斜截式

已知两点坐标

• 先求斜率，再代入任意坐标值求取截距

已知一点坐标和斜率

• 代入坐标值和斜率求取截距

已知斜率和截距

那还算什么，直接写了

043 线性方程的标准模式 - 一般式

标准形式

\(ax+by+c=0(最简形式，系数应为整数)\)

斜率-截距形式

\(y=mx+b\)

两种形式之间的相互转换

044 平行线和垂直线

平行线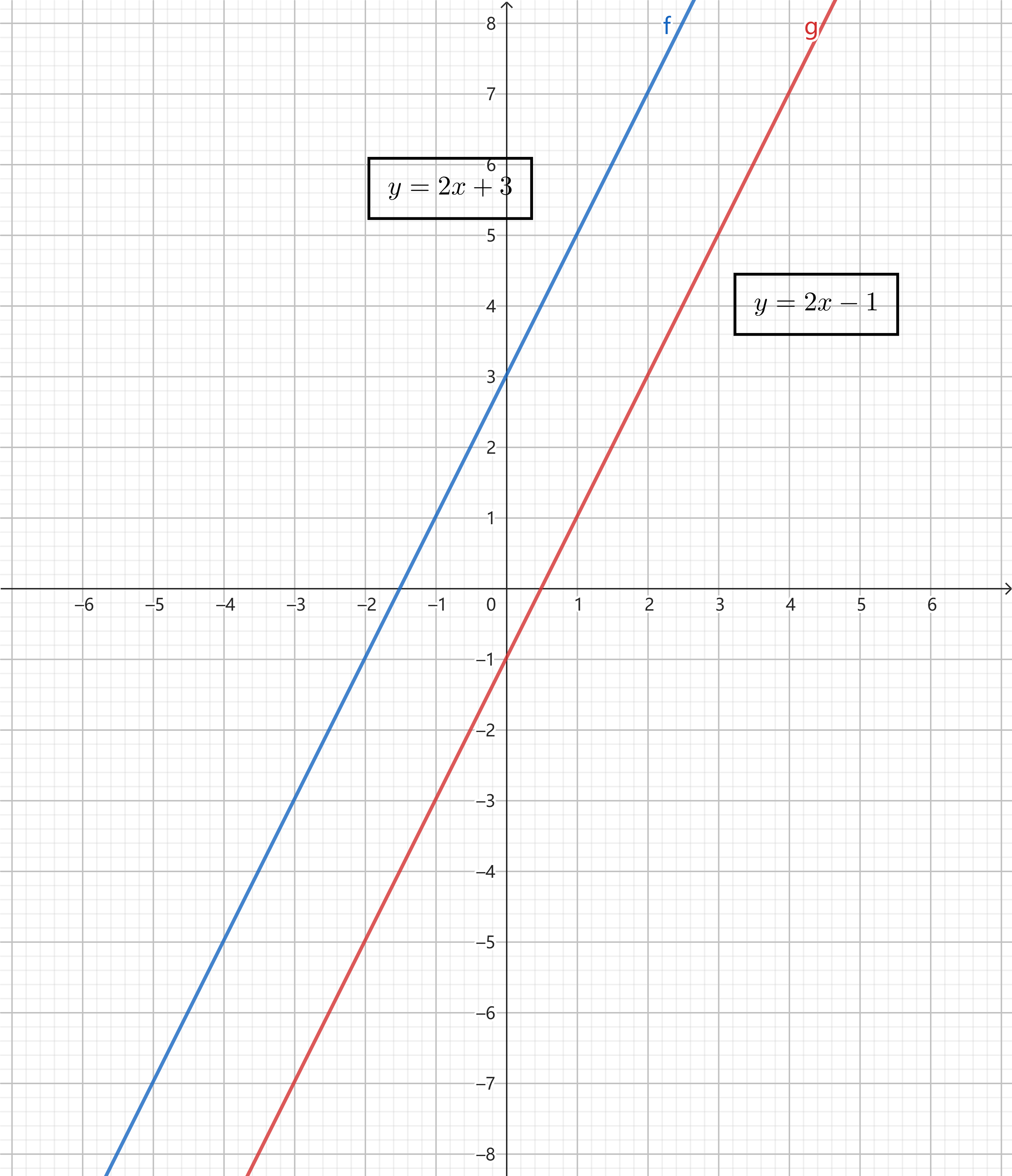

性质：两条线段的斜率相同，只是截距不同

垂直线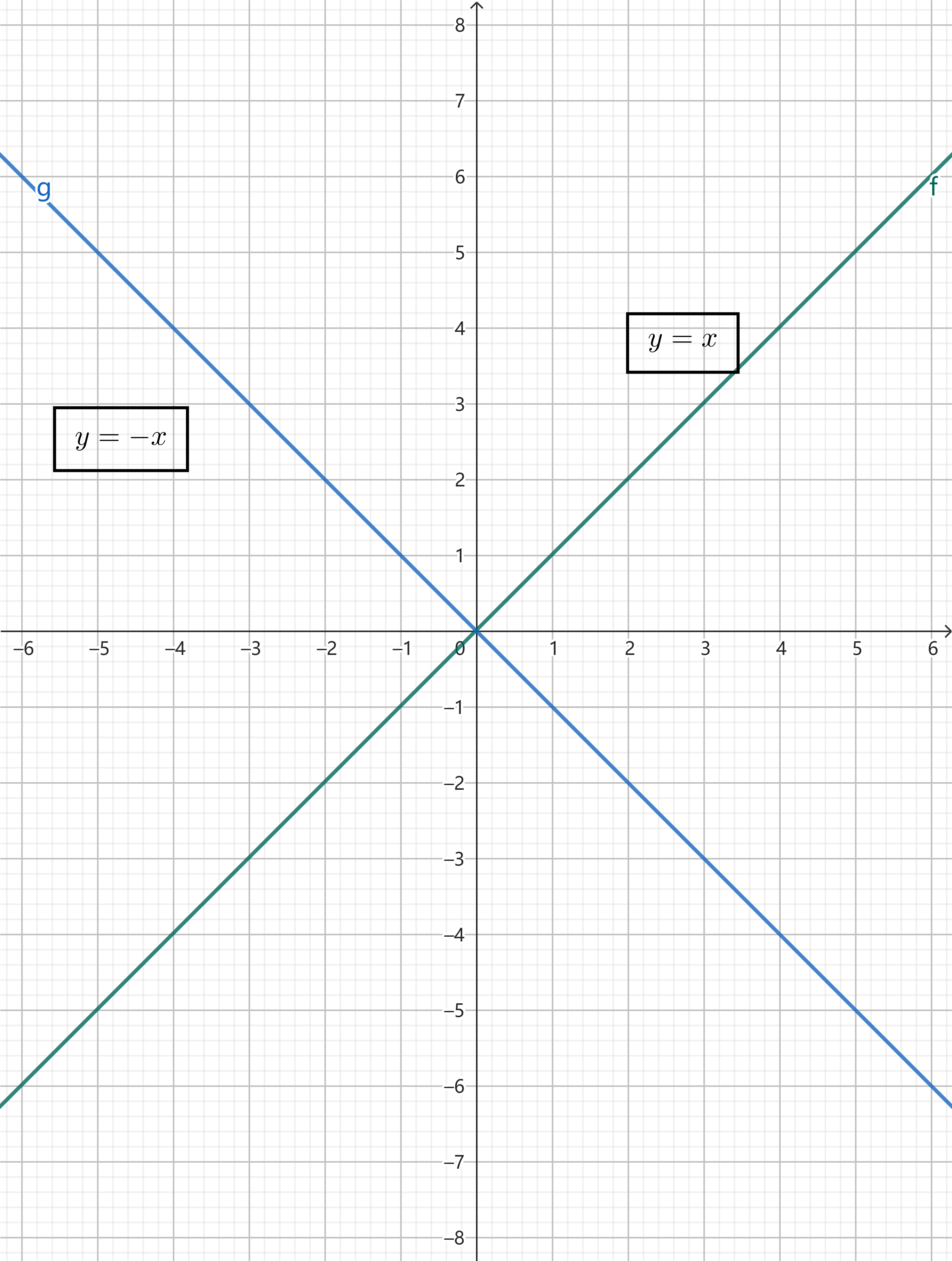

性质：斜率的乘积为-1（除了y轴和x轴这种，未定义的）

常见求解

• 已知与某线平行，且该线段经过某个点
  • 已知斜率和一点
• 已知与某线垂直，且该线段经过某个点
  • 已知斜率和线上一点

045 求解二元一次方程组

\[\begin{Bmatrix} 2x-1=9\\ x+y=36 \end{Bmatrix} \]

方法1：绘图，看两条线段的交点坐标

• 每条线上的点就是该方程的解

方法2：换元法

• 求y或者x，之后使用将(x/y)表达式放入到第二个方程中

方法3：消元法

• 要使得想要消除的未知数的系数相同或者相反,之后两个方程相加或相减

046 绝对值 绝对值方程求解 绝对值绘图

绝对值：|x|

表示的是x所表示的数距离0的距离。(使用数轴进行理解)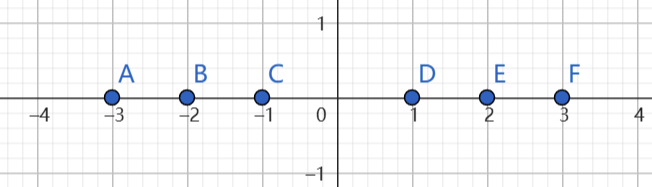

绝对值方程求解

• 去除绝对值的符号 需要分别求\(\pm\)情况
  \(|2x-1|=5\)

• \[\begin{Bmatrix} 2x-1=5\\ 2x-1=-5 \end{Bmatrix} \]

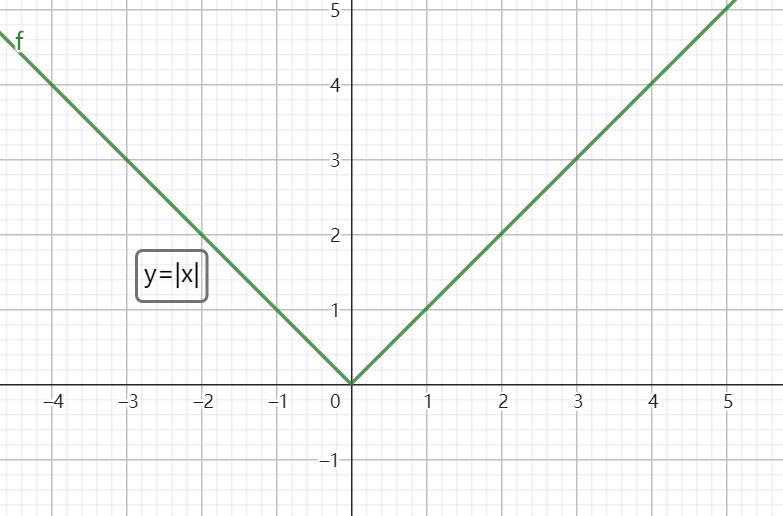
绝对值线性方程绘图

• 示例：y=|x|

  y的值绝不为负值，因此该线性方程所表示的线段在第一与第二象限

047 数字类型 实数与虚数 有理数与无理数

虚数：\(\sqrt{-1}=\imath\)(就念“i”)/\(\jmath\)

有理数：可以表示为两个整数比的数\(\frac{b}{a}(a\neq0)\);整数和整数分数统称为有理数(无限循环小数等：\(0.\bar{3}\))

无理数：有理数以外的实数（比如：\(\sqrt{2};\pi\)等无限不循环小数）

graph LR A[数字] --> B[实数] A --> C[虚数] B --> D[有理数] B --> E[无理数] D --> F[分数] D --> G[整数]

补充栏

因式分解-补充

法1：增添项

法2：长除法