10大现实多目标问题

ZZZ测试集问题分析

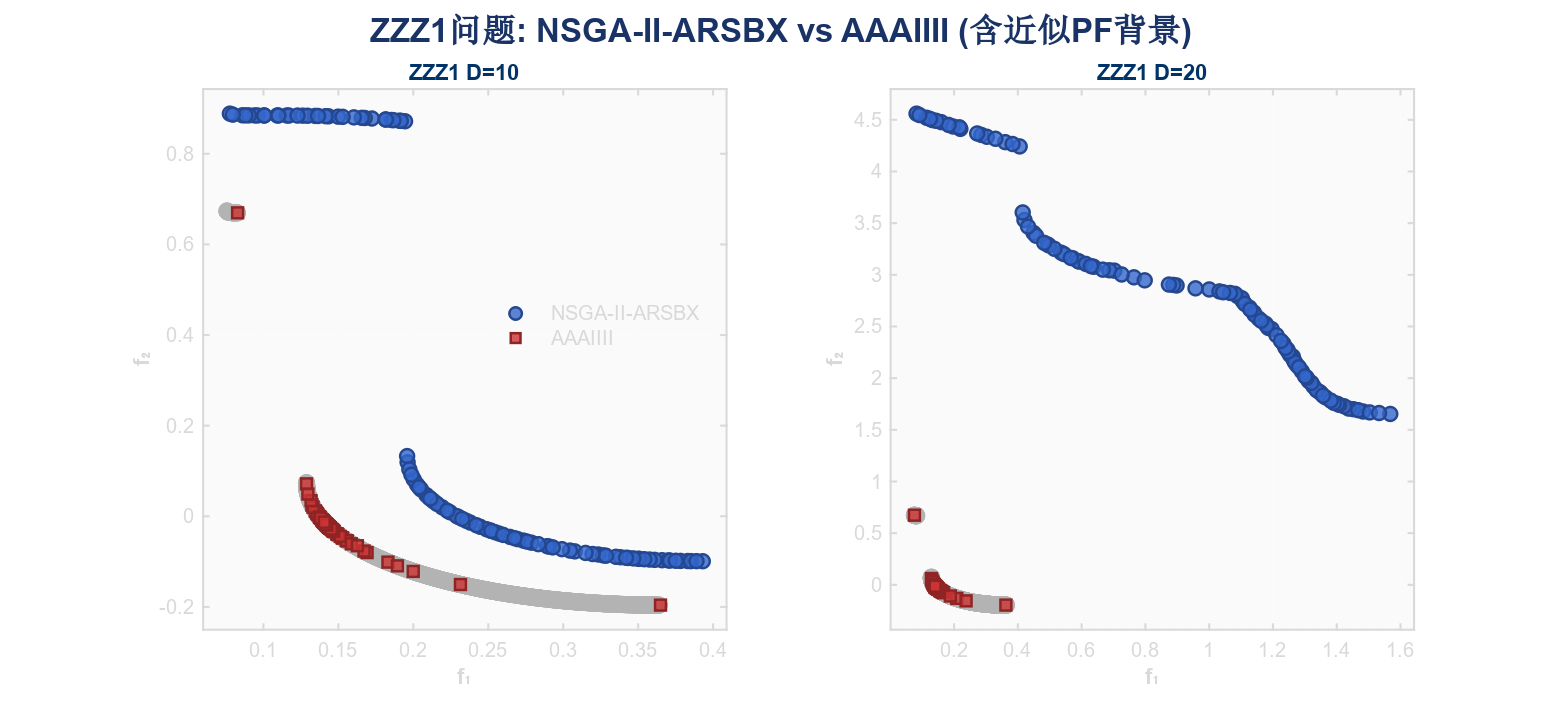
ZZZ1：非均匀权重和具有欺骗性局部Pareto前沿的问题

• 目标函数：
  • \(f_1 = x_1\)
  • \(f_2 = g \cdot (1 - \sqrt{f_1/g} - (f_1/g) \cdot \sin(10\pi f_1))\)
  • 非均匀权重：\(w_1 = 0.7 + 0.3\sin(6\pi x_1)\)，\(w_2 = 1 - w_1\)
  • 最终目标：\(F_1 = w_1 f_1 + (1-w_1)f_2\)，\(F_2 = w_2 f_1 + (1-w_2)f_2\)
• PF求解：未提供显式PF函数，通过GetOptimum采样。
• 现实应用：智能电网优化调度（PSO: Power System Optimization）。非均匀权重模拟不同时段电价或负荷优先级，欺骗性局部前沿反映不同调度策略下的次优解（如风电/光伏出力波动）。

---

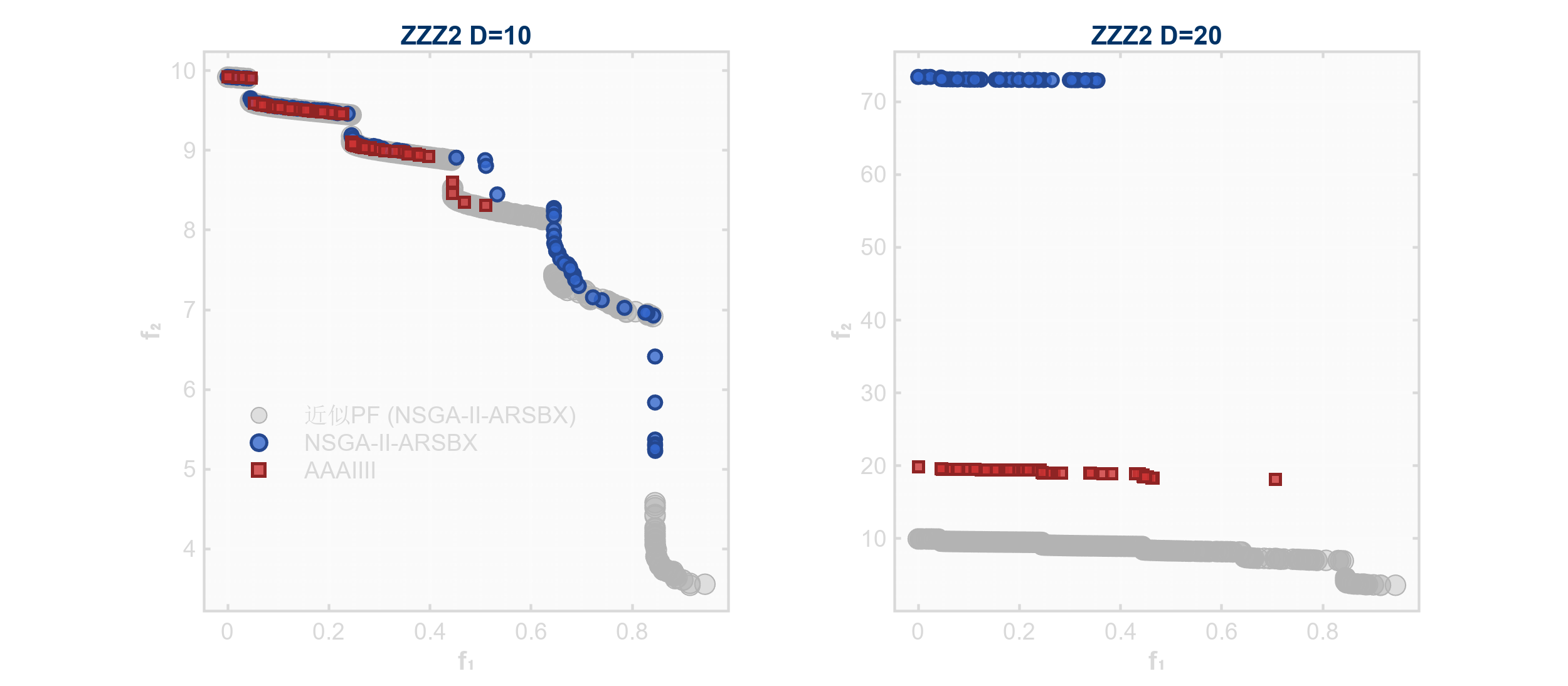
ZZZ2：多模态凹性多目标问题

• 目标函数：
  • \(f_1 = x_1 + 0.1\sin(10\pi x_1)\)（多模态）
  • \(g = 1 + \sum_{i=2}^D [100(x_i - x_{i-1}^2)^2 + (1-x_{i-1})^2]\)（类Rosenbrock函数）
  • \(f_2 = g \cdot (1 - (f_1/g)^2)\)
• PF求解：未提供显式PF函数，通过GetOptimum采样。
• 现实应用：机器人轨迹规划（RTP: Robot Trajectory Planning）。多模态对应多条可行路径，凹性前沿表示能耗与平滑性之间的权衡，Rosenbrock项模拟关节运动约束。

---

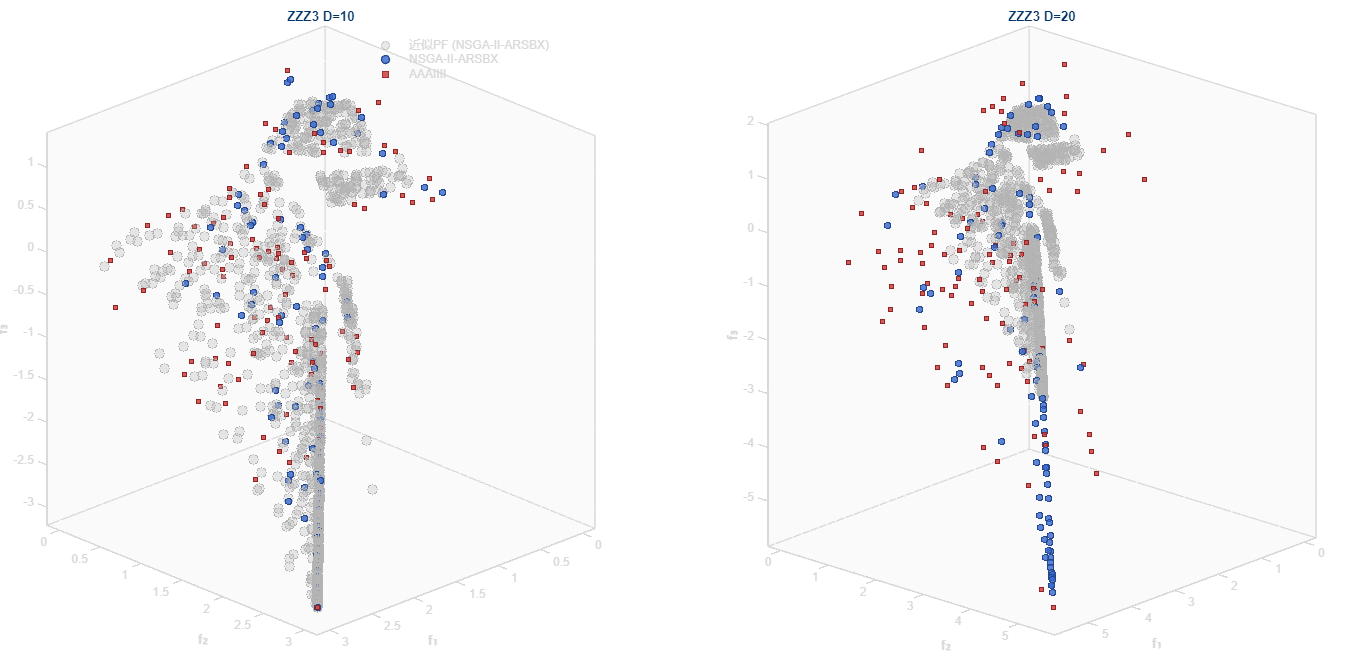
ZZZ3：分段耦合Mackey-Glass类问题（三目标）

• 目标函数：分三个区域：
  1. \(x_1<0.3\)：凸前沿（球面）
  2. \(0.3 \leq x_1 < 0.7\)：凹前沿（平面）
  3. \(x_1 \geq 0.7\)：线性前沿
• PF求解：分段解析形式，但未提供显式PF函数。
• 现实应用：多目标投资组合优化（MPT: Modern Portfolio Theory）。分段结构对应不同市场状态（牛市/熊市/震荡），球面区域表示高风险高回报，平面区域表示均衡配置，线性区域表示保守策略。

---

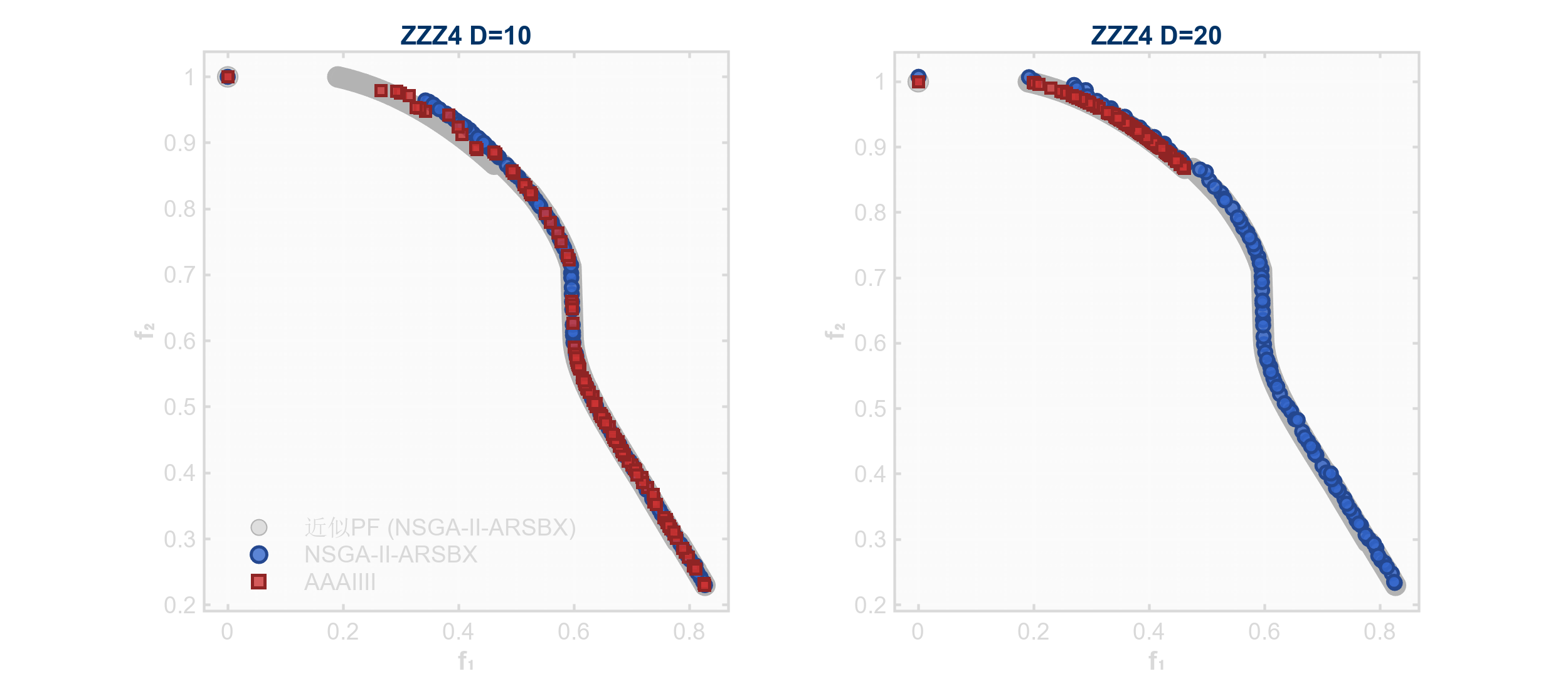
ZZZ4：时滞反馈动态优化问题

• 目标函数：
  • \(f_1 = \text{mean}(x_{\text{current}}) + 0.2 \cdot \text{feedback}\)
  • \(f_2 = (1 + 9 \cdot \text{mean}(x_{\text{delayed}})) \cdot (1 - f_1^2 + 0.1 \cdot \text{feedback})\)
  • 反馈项：\(\text{feedback} = \sin(2\pi \cdot \text{mean}(x_{\text{current}}, \text{mean}(x_{\text{delayed}})))\)
• PF求解：未提供显式PF函数，通过GetOptimum采样。
• 现实应用：网络流量控制（TCP: Transmission Control Protocol）。时滞模拟网络延迟，反馈对应拥塞窗口调整，目标是最小化延迟与最大化吞吐量。

---

ZZZ5：偏置缩放非均匀密度问题

• 目标函数：
  • \(f_1 = x_1^2\)
  • \(g\)：分段函数（\(x_i<0.5\)为平方惩罚，否则为四次惩罚）
  • \(f_2 = g \cdot e^{-2f_1/g} \cdot (1 + 0.1\cos(10\pi f_1))\)
• PF求解：提供解析PF：\(f_1 \in [0,1]\)，\(f_2 = e^{-2f_1} \cdot (1 + 0.1\cos(10\pi f_1))\)（当\(x_i=0.5, i>1\)）。
• 现实应用：无线传感器网络部署（WSN Deployment）。偏置缩放反映热点区域覆盖密度，非均匀密度对应能耗与覆盖率的权衡。

---

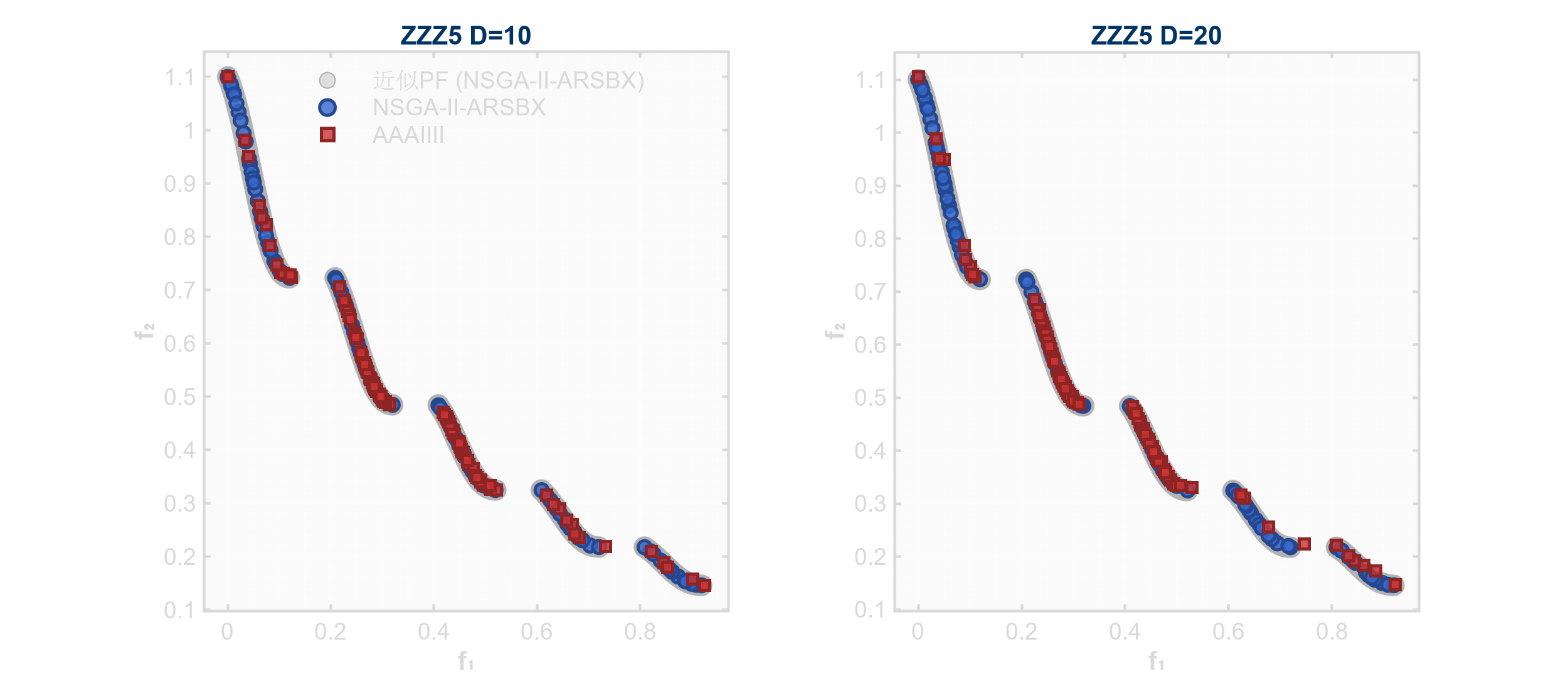
ZZZ6：凸不连续多目标问题

• 目标函数：
  • \(f_1 = x_1\)
  • \(g = 1 + 9 \cdot \text{mean}(x_{2:D})\)
  • \(f_2 = g \cdot (1 - \sqrt{f_1/g} - (f_1/g) \cdot \sin(5\pi f_1))\)
• PF求解：提供解析PF：\(f_1 \in [0,1]\)，\(f_2 = 1 - \sqrt{f_1} - f_1 \cdot \sin(5\pi f_1)\)（当\(x_i=0, i>1\)）。
• 现实应用：云计算任务调度（CTS: Cloud Task Scheduling）。不连续前沿对应任务抢占或资源中断，凸段表示不同VM配置下的成本-时间权衡。

---

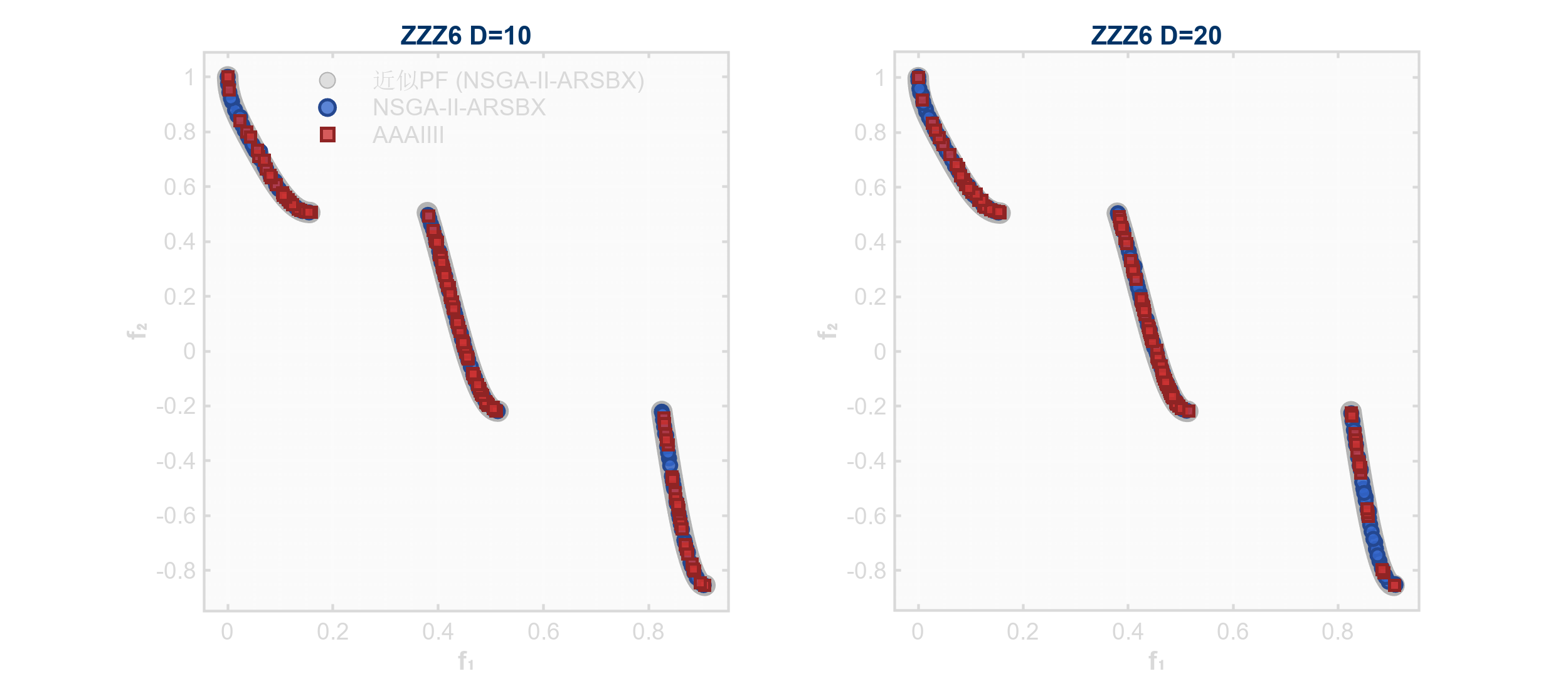
ZZZ7：非对称线性-二次多目标问题

• 目标函数：
  • \(f_1 = x_1\)
  • \(g\)：区域依赖（\(x_1<0.3\)为平方，\(0.3 \leq x_1 < 0.7\)为绝对值，否则为四次）
  • \(f_2 = g \cdot (1 - f_1/g - 0.2\sin(3\pi f_1))\)
• PF求解：提供近似PF：\(f_1 \in [0,1]\)，\(f_2 = 1 - f_1 - 0.2\sin(3\pi f_1)\)（假设\(x_i\)取区域最优值）。
• 现实应用：供应链多级库存优化（MISO: Multi-echelon Inventory System Optimization）。非对称性表示不同仓库级别的成本结构，区域依赖对应安全库存策略。

---

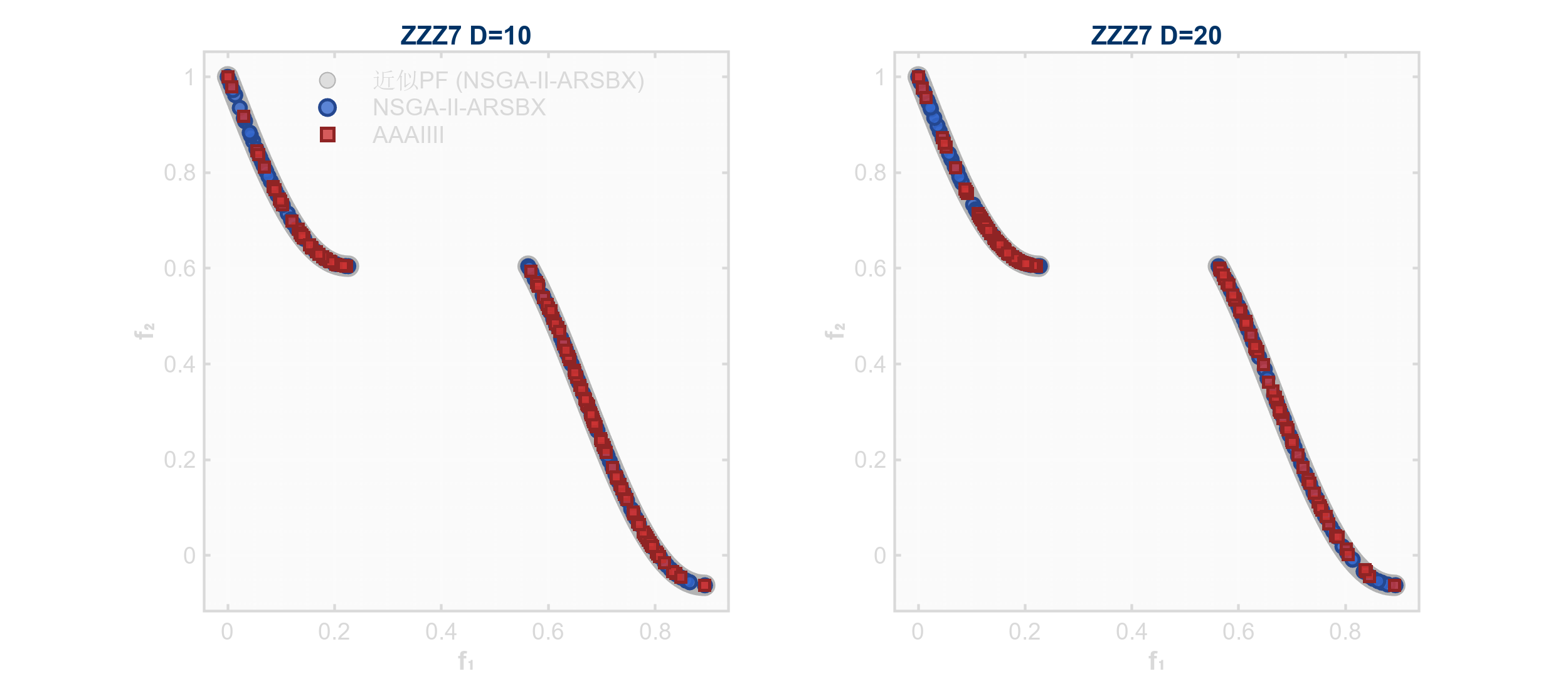
ZZZ8：自适应惩罚Shekel函数扩展

• 目标函数：基于Shekel函数（多峰）：
  • \(f_1, f_2 = \sum_{i=1}^5 \frac{1}{A_{i,k}(x-C_{i,k})^2 + \ldots + 1}\)
  • 自适应惩罚项：\(penalty = 1 + 9 \cdot \text{mean}(x_{2:D})\)
  • 最终目标：加权和 \(F_k = (1-penalty) \cdot f_k + penalty \cdot \text{term}_k\)
• PF求解：提供PF：\(f_1 = x_1\)，\(f_2 = 1 - x_1^2\)（当\(x_i=0.5, i>1\)），但局部最优点被删除。
• 现实应用：化学过程多目标优化（CPO: Chemical Process Optimization）。Shekel函数模拟反应釜多稳态，自适应惩罚对应环保约束，局部前沿表示不同催化剂配比。

---

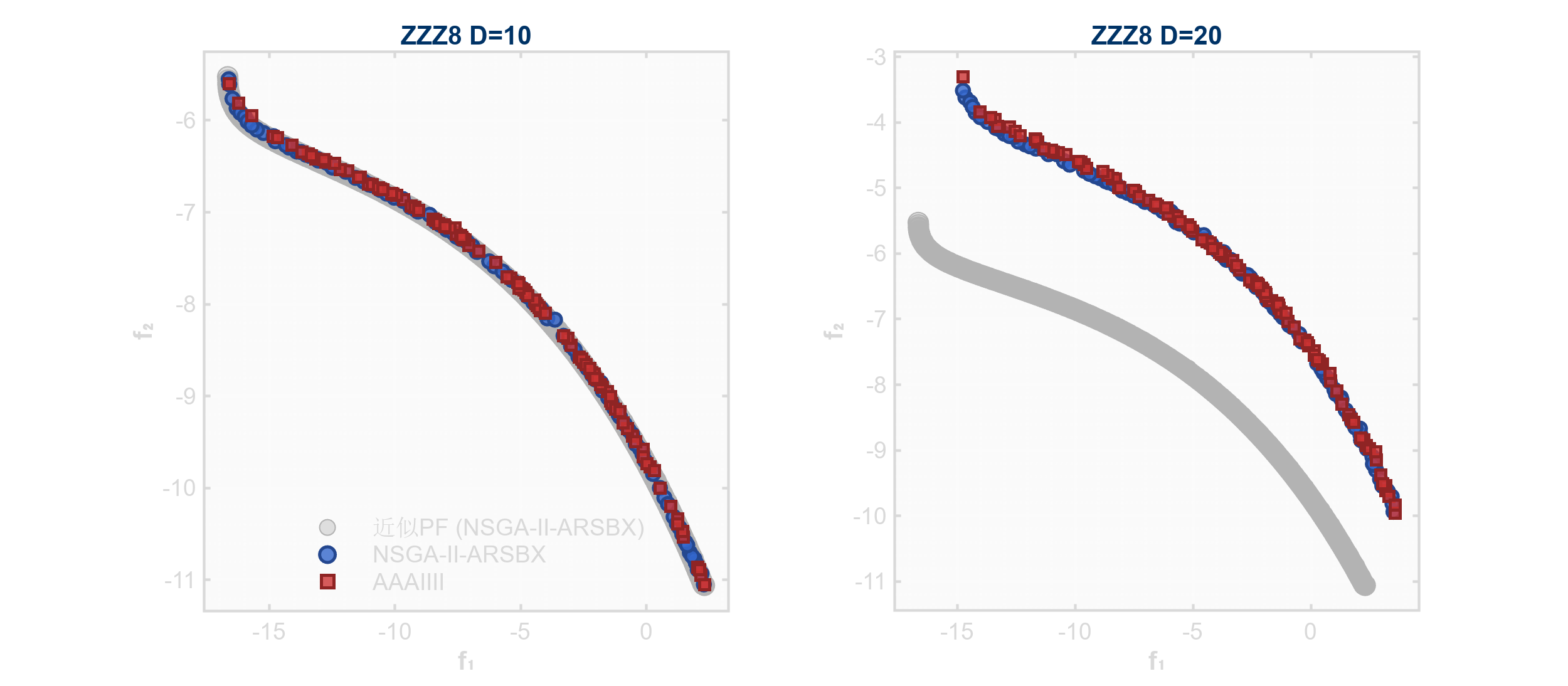
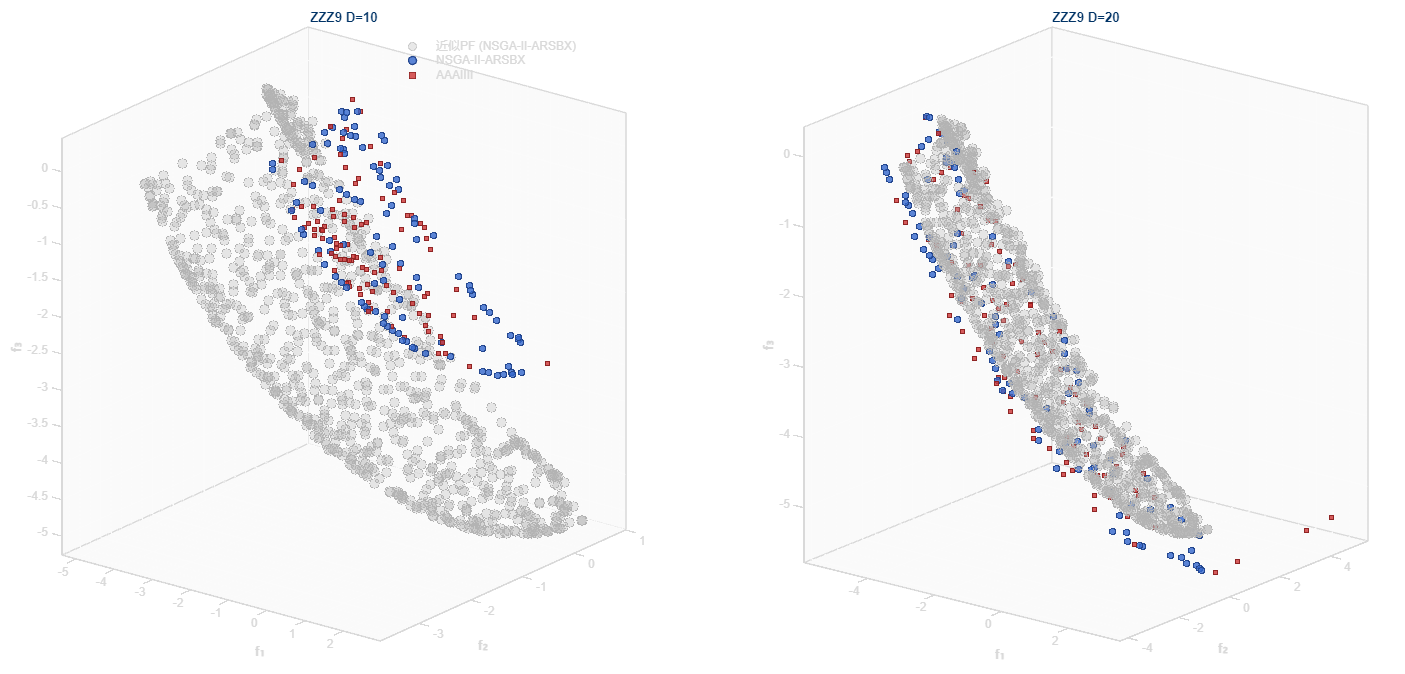
ZZZ9：混合变量复杂耦合问题（多目标/三目标）

• 目标函数：
  • 非线性变换：\(\theta=2\pi x_1\)，\(\phi=\pi x_2/2\)
  • 指数权重：\(\alpha=e^{-5|x_1-0.5|}\)，\(\beta=e^{-5|x_2-0.5|}\)
  • \(f_1 = (1+g)[\alpha \cos\theta \cos\phi + (1-\alpha)x_1] + \text{扰动}\)
  • \(f_2 = (1+g)[\beta \cos\theta \sin\phi + (1-\beta)x_2] + \text{扰动}\)
  • \(f_3 = (1+g)\sin\theta\)
• PF求解：通过球面坐标采样并应用非线性变换生成PF。
• 现实应用：航空航天器多学科设计优化（MDO: Multidisciplinary Design Optimization）。复杂耦合模拟气动-结构-控制交互，指数权重表示设计约束的急剧变化，扰动模拟制造公差。

---

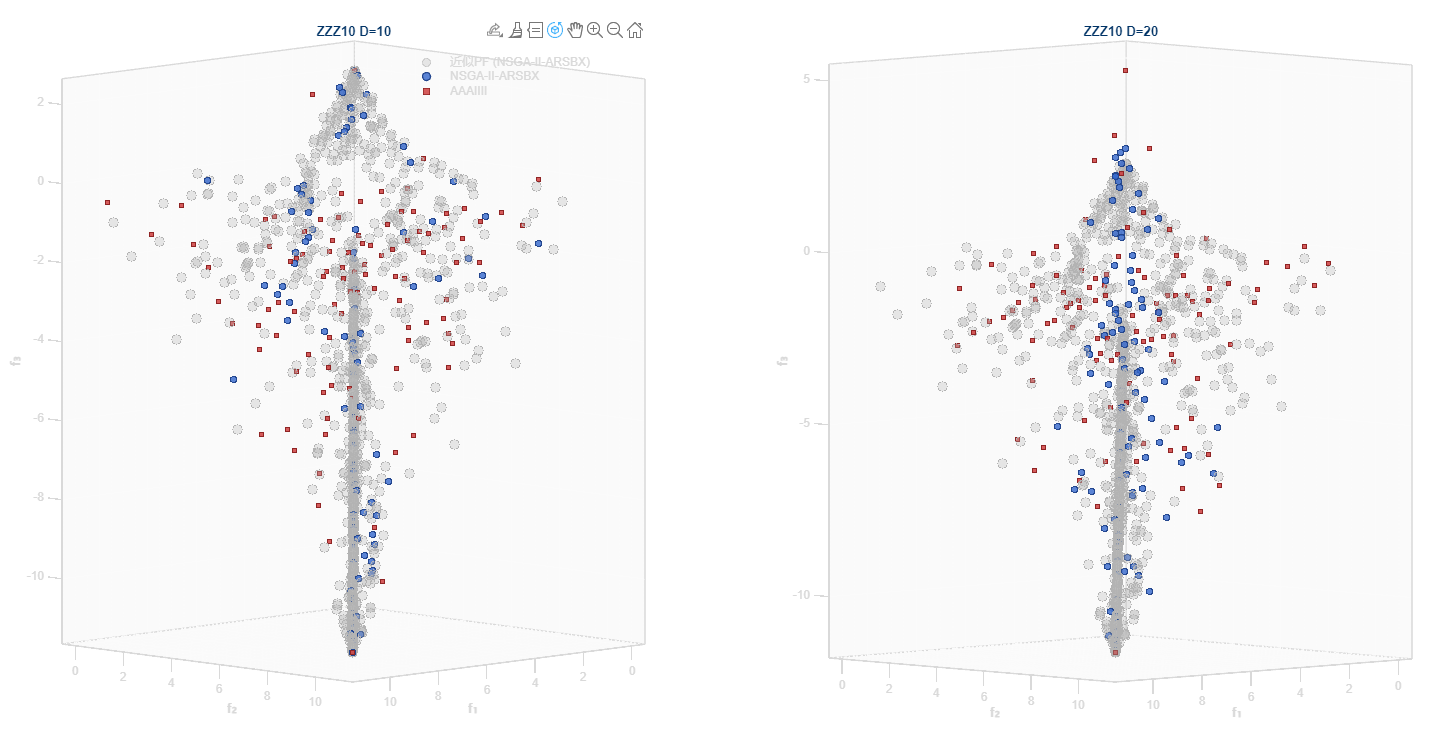
ZZZ10：三目标退化问题（二维Pareto前沿）

• 目标函数：
  • \(f_1 = (1+g) \cdot x_1\)
  • \(f_2 = (1+g) \cdot x_2\)
  • \(f_3 = (1+g) \cdot (1 - x_1 - x_2)\)
  • 约束：\(f_1 + f_2 + f_3 = 1+g\)
• PF求解：PF是三维空间中的二维三角平面，通过均匀采样三角形生成。
• 现实应用：资源分配中的三目标权衡（RAM: Resource Allocation in Multimedia Systems）。例如视频编码中的码率、分辨率、帧率三目标优化，退化前沿表示三者之和恒定。