左右手（直角）坐标系叉乘计算公式
左右手（直角）坐标系叉乘计算公式
右手坐标系下叉乘公式
设右手坐标系基为\(\{\vec{i},\vec{j},\vec{k}\}\)，并满足以下条件:
\[\vec{i}\times\vec{i} =\vec{j}\times\vec{j} =\vec{k}\times\vec{k} =\vec{0}
\]
\[\vec{i}\times\vec{j}=-\vec{j}\times\vec{i} =\vec{k}
\]
\[\vec{k}\times\vec{i} =-\vec{i}\times\vec{k} =\vec{j}
\]
\[\vec{j}\times\vec{k} =-\vec{k}\times\vec{j} =\vec{i}
\]
并设\(\vec{v_1},\vec{v_2}\)如下：
\[\vec{v_1}=\begin{pmatrix}\vec{i} & \vec{j} & \vec{k}\end{pmatrix}\begin{pmatrix}x_1 \\ y_1 \\ z_1\end{pmatrix}=x_1\vec{i} + y_1\vec{j} + z_1\vec{k}
\]
\[\vec{v_2}=\begin{pmatrix}\vec{i} & \vec{j} & \vec{k}\end{pmatrix}\begin{pmatrix}x_2 \\ y_2 \\ z_2\end{pmatrix}=x_2\vec{i} + y_2\vec{j} + z_2\vec{k}
\]
则\(\vec{v_1}\times \vec{v_2}\)为：
\[\vec{v_1}\times \vec{v_2}
=(x_1\vec{i} + y_1\vec{j} + z_1\vec{k})\times(x_2\vec{i} + y_2\vec{j} + z_2\vec{k})
\]
\[=\begin{vmatrix}\vec{j}\times\vec{k} & \vec{k}\times\vec{i} & \vec{i}\times\vec{j} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2\end{vmatrix}
=\begin{vmatrix}\vec{i} & \vec{j} & \vec{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2\end{vmatrix}
\]
左手坐标系下叉乘公式
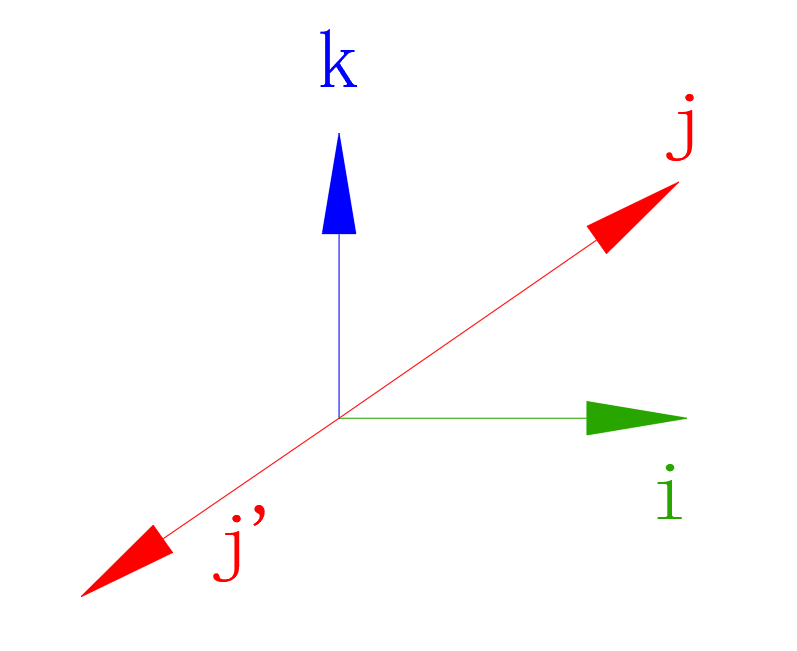
设左手坐标系基为\(\{\vec{i},\vec{j'},\vec{k}\}\)，其中\(\vec{j'}=-\vec{j}\)，并满足以下条件:
\[\vec{i}\times\vec{i} =\vec{j'}\times\vec{j'} =\vec{k}\times\vec{k} =\vec{0}
\]
\[\vec{i}\times\vec{j'}=-\vec{j'}\times\vec{i} =-\vec{k}
\]
\[\vec{k}\times\vec{i} =-\vec{i}\times\vec{k} =-\vec{j'}
\]
\[\vec{j'}\times\vec{k} =-\vec{k}\times\vec{j'} =-\vec{i}
\]
并设\(\vec{v_1},\vec{v_2}\)如下：
\[\vec{v_1}=\begin{pmatrix}\vec{i} & \vec{j'} & \vec{k}\end{pmatrix}\begin{pmatrix}x_1' \\ y_1' \\ z_1'\end{pmatrix}=x_1'\vec{i} + y_1'\vec{j'} + z_1'\vec{k}
\]
\[\vec{v_2}=\begin{pmatrix}\vec{i} & \vec{j'} & \vec{k}\end{pmatrix}\begin{pmatrix}x_2' \\ y_2' \\ z_2'\end{pmatrix}=x_2'\vec{i} + y_2'\vec{j'} + z_2'\vec{k}
\]
则\(\vec{v_1}\times \vec{v_2}\)为：
\[\vec{v_1}\times \vec{v_2}
=(x_1'\vec{i} + y_1'\vec{j'} + z_1'\vec{k})\times(x_2'\vec{i} + y_2'\vec{j'} + z_2'\vec{k})
\]
\[=\begin{vmatrix}-\vec{i} & -\vec{j'} & -\vec{k} \\ x_1' & y_1' & z_1' \\ x_2' & y_2' & z_2'\end{vmatrix}=-\begin{vmatrix}\vec{i} & \vec{j'} & \vec{k} \\ x_1' & y_1' & z_1' \\ x_2' & y_2' & z_2'\end{vmatrix}=\begin{vmatrix}\vec{i} & \vec{j} & \vec{k} \\ x_1' & -y_1' & z_1' \\ x_2' & -y_2' & z_2'\end{vmatrix}
\]
左手系下计算左手系坐标：
\[\vec{v_1}\times \vec{v_2}
=-\begin{vmatrix}\vec{i} & \vec{j'} & \vec{k} \\ x_1' & y_1' & z_1' \\ x_2' & y_2' & z_2'\end{vmatrix}
\]
左手系下计算右手系坐标：
\[\vec{v_1}\times \vec{v_2}
=\begin{vmatrix}\vec{i} & \vec{j} & \vec{k} \\ x_1' & -y_1' & z_1' \\ x_2' & -y_2' & z_2'\end{vmatrix}
\]
左手系坐标与右手系坐标之间关系
\[\begin{pmatrix}x_1' \\ y_1' \\ z_1'\end{pmatrix}
=\begin{pmatrix}e_1 & -e_2 & e_3\end{pmatrix}\begin{pmatrix}x_1 \\ y_1 \\ z_1\end{pmatrix}
=\begin{pmatrix}1 & 0 & 0\\0 & -1 & 0\\0 & 0 & 1\end{pmatrix}\begin{pmatrix}x_1 \\ y_1 \\ z_1\end{pmatrix}
=\begin{pmatrix}x_1 \\ -y_1 \\ z_1\end{pmatrix}
\]
同理，\(\begin{pmatrix}x_1 \\ y_1 \\ z_1\end{pmatrix}=\begin{pmatrix}x_1' \\ -y_1' \\ z_1'\end{pmatrix}\)
从而，左手系叉乘法
\[\vec{v_1}\times \vec{v_2}
=\begin{vmatrix}\vec{i} & \vec{j} & \vec{k} \\ x_1' & -y_1' & z_1' \\ x_2' & -y_2' & z_2'\end{vmatrix}
=\begin{vmatrix}\vec{i} & \vec{j} & \vec{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2\end{vmatrix}
\]
