P8340 [AHOI2022] 山河重整
\(20pts\) 给 \(O(2^n)\) 枚举,\(60pts\) 是 \(O(n^2)\),先看看怎么做。计数题无非容斥和 \(dp\),不妨从 \(dp\) 入手。多项式复杂度的做法意味着无法将 \([1,n]\) 中是否能全部被表示直接存入状态,考虑将其转化为另一个充要条件,注意到:
- \(\forall i\in [1,n]\),需要满足 \(S\) 中 \(\le i\) 的元素之和 \(\ge i\)。
证明:必要性显然,考虑使用数学归纳法证明其必要性。\(i=1,2\) 时显然,对于 \(i \ge 3\),假设找到最小的 \(x\) 使得 \(\le x\) 的值相加的和 \(\ge i\),设这个和为 \(s\),则有 \(s \lt 2i\)(否则由于 \(x \le i\) 则 \(x\) 不是最小),而又有 \(i \le s\),所以 \(s - i \lt i\),由于 \(\lt i\) 的可以被表示,所以 \(\gt s - i\) 的也可以,即 \(\ge i\) 的可以被表示,证毕。
于是进行 \(O(n^2)\) 的背包 \(dp\),可以获得 \(60pts\),具体做法不再赘述。
然而这个状态不太好优化。思考完 \(dp\),来考虑容斥(正难则反),即考虑不合法的情况有多少种。显然可以找到最小的 \(x\) 使得 \(S\) 中 \(\le x\) 的元素之和 \(\lt x\),将其方案数从总和内减去。又发现,若 \(\le x\) 的元素之和 \(\lt x\) 且 \(x\) 最小,则 \(\le x-1\) 的元素之和必定 \(=x-1\)。如此一来,不妨设 \(f_i\) 为 \(\le i\) 的元素之和为 \(i\) 并且任意 \(x \le i\) 都合法的方案数,状态数量被优化为线性。
那么,问题转化为如何快速求出 \(f_i\),同样可以容斥,用总方案数减去不合法的情况。总方案数就是 \(i\) 的整数拆分方案数,这个后面会讲。而不合法的方案数就是全局不合法方案的一部分,可以通过 \(f_{1\cdots i-1}\) 计算出。
现在考虑对一个数 \(n\) 进行整数拆分的方案数,一个 trivial 的想法是使用 \(O(n^2)\) 的背包。注意到背包的第二维值域为 \(n\),而由于每次第二维要加上 \(i\),使得增长速度很快,所以只会进行 \(\sqrt n\) 次第二维的增加操作,这给了我们优化的空间。
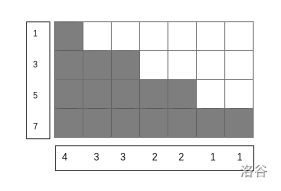
可以通过下图便于理解。行代表从小到大加入的不同的数,由于总方格数量为 \(n\),所以行数是 \(O(\sqrt n)\) 级别的。但如果按照一行一行地做就不免要枚举第一维加入的 \(i\) 以及第二维的总和,复杂度是 \(O(n^2)\)。换一种思路,一列一列地做,相当于对 \([1,\sqrt{2n}] \cap \mathbb{Z}\) 做类似完全背包,并且为了保证每行互不相同,就需要让加入的数是连续的,只需要在 \(dp\) 时多留心一下,就得到了 \(O(n\sqrt n)\) 计算整数拆分的算法。
考虑前面的 \(f_j\) 对后面 \(f_i\) 的贡献,根据 \(f_j\) 的定义,一定有 \(j+1\) 没法被表示,所以 \(j+(j+2) \le i\),同时要求 \([j+2,i]\cap S\) 的总和 \(s+j=i\)。类似于整数拆分,枚举新加入的列即可。如此一来,想要算出 \(f_i\) 就要求前面的 \(f_j\) 值已经确定。
考虑到 \(j \le \frac{i}{2}\),可以通过类似于分治的方法,先计算出 \(f_{1\cdots n/2}\),然后在 \(O(n \sqrt n)\) 的复杂度内贡献到 \(f_{n/2\cdots n}\) 中。总的时间复杂度为 \(T(n) = O(n \sqrt n) + T(n / 2) = O(n \sqrt n)\)。
代码如下:
int n, p, pw2[MAXN], f[MAXN], g[MAXN];
inline void add(int& x, int y) { x += y, x >= p && (x -= p); }
void solve(int n) {
if (n <= 1) return void(f[0] = 1);
solve(n >> 1);
for (int i = 0; i <= n; ++i) g[i] = 0;
for (int i = sqrt(n * 2); i >= 1; --i) {
for (int j = n; j >= i; --j) g[j] = g[j - i];
for (int j = 0; j + (j + 2) * i <= n; ++j) add(g[j + (j + 2) * i], f[j]);
for (int j = i; j <= n; ++j) add(g[j], g[j - i]);
}
for (int i = n / 2 + 1; i <= n; ++i) if (g[i]) add(f[i], p - g[i]);
}
signed main() {
read(n), read(p), pw2[0] = 1;
for (int i = 1; i <= n; ++i) pw2[i] = 2ll * pw2[i - 1] % p;
for (int i = sqrt(n * 2); i >= 1; --i) {
for (int j = n; j >= i; --j) f[j] = f[j - i];
add(f[i], 1);
for (int j = i; j <= n; ++j) add(f[j], f[j - i]);
}
solve(n);
int ans = pw2[n];
for (int i = 0; i < n; ++i)
add(ans, p - (ll)f[i] * pw2[n - i - 1] % p);
write(ans), putchar('\n');
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号