力扣-494-目标和

官解的思路是这样的
假设数组元素总和为sum，其中添加“-”号的元素和为neg
那么target=添加+号的元素和-添加-号的元素和=(sum-neg)-neg=sum-2neg
移项可以得到：neg=(sum-target)/2

那么题目就变成了：从数组中挑元素，使其和为(sum-target)/2，有几种可能？

定义dp[i][j]为从前i个元素中取，使之总和等于j的种数

这边留两个空行方便理解，两个0行全部置0

很明显是个二维dp，但是j可以只取到neg，那么这个dp是怎么状态转移的呢？

PS：accumulate()第三个参数是要计算的初始值，一般应该填0

	int n = nums.size();
	int sum = accumulate(nums.begin(), nums.end(),0);
	int neg = 0;
	// 剪枝，如果不存在整数neg，则不存在
	if ((sum - target) % 2 == 0) neg = (sum - target) / 2;
	else return neg;
 
	vector<vector<int>> dp(n + 1, vector<int>(neg + 1,0));
	// 没有元素可选时，和为0
	dp[0][0] = 1;
 
	for (int i = 1; i < n + 1; i++) 
		for (int j = 0; j < neg + 1; j++) 
			// 因为要和为j，所以如果有大于j的一定不能要
			if (nums[i - 1] > j) dp[i][j] = dp[i - 1][j];
			// 如果小于j，等于有这个num能凑成的加上没这个num能凑成的
			else dp[i][j] = dp[i][j - nums[i - 1]] + dp[i - 1][j];
		// 这个过程画出来跟背包差不多
 
	return dp[n][neg];
}

这么写有问题就是，第一行初始化了，但是第一列没有，如果这里
dp[i][j] == dp[i][j - nums[i - 1]]
那么初始值就特别重要了，所以还是要考虑第一列的初始化，==不只是dp[0][0]=1，只要是等于0的dp[i][0]都等于1

	for (int i = 1; i < n + 1; i++)
		for (int j = 0; j < neg + 1; j++)
			// 对第一列的初始化
			if (j == 0 && nums[i - 1] == 0) dp[i][j] = 1;
			// 因为要和为j，所以如果有大于j的一定不能要
			else if (nums[i - 1] > j) dp[i][j] = dp[i - 1][j];
			// 如果小于j，等于有这个num能凑成的加上没这个num能凑成的
			else dp[i][j] = dp[i][j - nums[i - 1]] + dp[i - 1][j];
		// 这个过程画出来跟背包差不多

然后，这初始化还不能这样写到里面去了？！
但是这样写到外面很不优雅，还会有额外的遍历

	for (int i = 0; i < n + 1; i++) if (nums[i] == 0) dp[i][0] = 1;

其实不是不能写到里面去，而是不能写成if-else

也不对，这里不是简单地初始化为1

我之前以为这么写

			if (nums[i - 1] > j) dp[i][j] = dp[i - 1][j];
			else dp[i][j] = dp[i][j - nums[i - 1]] + dp[i - 1][j];

和这么写，本质上没区别，但其实不是的！！

			dp[i][j] = dp[i - 1][j];
			if (nums[i - 1] <= j) dp[i][j] += dp[i][j - nums[i - 1]];

第二种写法的第一句是重要的初始化过程，因为j没变，所以先把前面i-1个继承过来

啊，然后又错了，这里是i-1

			if (nums[i - 1] <= j) dp[i][j] += dp[i-1][j - nums[i - 1]];

因为这里加上的是选了num的情况，状态转移中不应该包括num

天！！这是来恶心我的吧

做空间优化，只需要上一行，01背包的空间优化是从后往前的

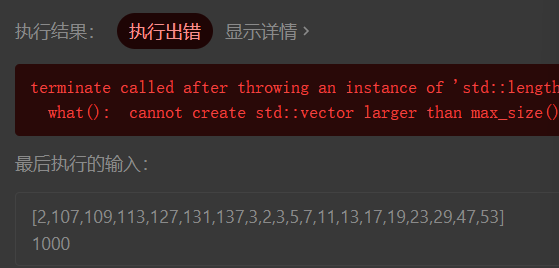
[2,107,109,113,127,131,137,3,2,3,5,7,11,13,17,19,23,29,47,53]
1000

这个测试用例有点怪，我以为是数组太长了，虽然我觉得这不太可能，然后断点发现sum-target居然是个负数

这就是在坑我了，坑我没检查参数

int findTargetSumWays(vector<int>& nums, int target) {
	int n = nums.size();
	int sum = accumulate(nums.begin(), nums.end(),0);
	int neg = 0;
	// 剪枝，如果不存在整数neg，则不存在
	if ((sum - target) % 2 != 0 || (sum - target) < 0) return neg;
	else neg = (sum - target) / 2;
 
	vector<int> dp(neg + 1, 0);
	dp[0] = 1;
 
	for (int i = 1; i < n + 1; i++)
		for (int j = neg; j >= 0; j--) {
			dp[j] = dp[j];
			if (nums[i - 1] <= j) dp[j] += dp[j - nums[i - 1]];
		}
	// 这个过程画出来跟背包差不多
 
	return dp[neg];
}

这就是最终版本了，WA了4次
下次回头试试回溯