剑指Offer-15-二进制中1的个数/力扣191-位1的个数

位运算

基础概念

1. 与：&（有0为0）
2. 或：|（有1为1）
3. 异或：^（相同0，不同1）
4. 非：~（取反）
5. 左移：相当于乘2；在左移n位时，最左边的n位将被丢弃，右边补上n个0
6. 右移：相当于除2；在右移n位时，最右边的n位将被丢弃，左边补位分为两种情况，无符号数补0，有符号数补符号位（1）

使用技巧

1. 判奇偶

(x&1)：将被测数与1做”与“运算，判断数的（二进制）最后一位是0还是1

string judge(int num) {
    // 比较运算符的优先级高于位运算符号
    if ((num & 1) == 0) {
        // 数的二进制末位为0
        // 那么这里就有一个隐式的”转二进制“操作？
        return "even";
    }
    else {
        return "odd";
    }
}

int main()
{
    cout << judge(100) << endl;
    cout << judge(7) << endl;
    cout << judge(-4) << endl;

    return 0;
}

2. 不适用额外变量，交换两数

void swap(int &a, int &b) {
    a ^= b;
    b ^= a;
    // b=b^a=b^(a^b)=(b^b)^a=0^a=a
    // 一个数异或0等于它本身
    a ^= b;
    // a=a^b=(a^b)^a=0^b=b
}

int main()
{
    int a = 1, b = -8;
    swap(a, b);
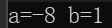
    cout << "a=" << a << " b=" << b;
    //cout << (7 ^ 2);// =5？
    // 两个不同的数异或=无进制加法
    // 二进制111^10=101=5

    return 0;
}

3. 异或可以被当做无进位加法使用，与操作可以用来获取进位

剑指Offer-65-不用加减乘除做加法

题目

可能引起死循环的解法

书上给出了一种可能引起死循环的解法，是这样的：

1. 判断低位是否为1
2. 将数右移一位
3. 重复以上步骤
   引起死循环的原因则是，当二进制数为负数时，右移操作后高位便会补1，最终数字变成全是1（0xFFFFFFFF）并持续进行下去

常规解法

为了避免上面的情况发生，那么不要右移原数字，而是左移1（由低到高用来”与“每一位来判1）

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;
        unsigned int flag =1;
        // 循环次数等于整数二进制的位数
        // 即1从低位移到了高位
        while(flag){
            if(n&flag) count++;
            // 当与运算结果为1，即当前位为1
            // 与运算是默认和低位进行的吗？
            // 不是二进制则转换成二进制在进行运算吗
            flag<<=1;
        }
        return count;
    }
};

但很明显，大多数情况下执行了不必要的循环次数

最优解

分析到一种情况，将一个二进制数减一，则：

• 最右边的1变为0，它右边有0则变1，左边不变
  在与原整数做”与运算“

总结下来是：把一个整数减一再与原整数做”与“运算=把该整数最右边的1变为0
那么有多少个1就可以进行多少次这样的操作了

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count = 0;
        while(n){
            // 当原整数中所有的1都变成0的时候，循环结束
            ++count;
            n=(n-1)&n;// 相当于把最右边的1变为0
        }
        return count;
    }
};

就是用某种位操作消从最右边开始消1