Occ 求点到直线的距离

计算一个点到2d基本曲线的距离使用这个类Extrema_ExtPElC2d。距离可以是最小或者最大。

Extrema是极值的意思，P是point点，ELC是elementary curve基本曲线。

 

点到直线的距离

假设一个点 Y 和一条直线 L

 

 

 

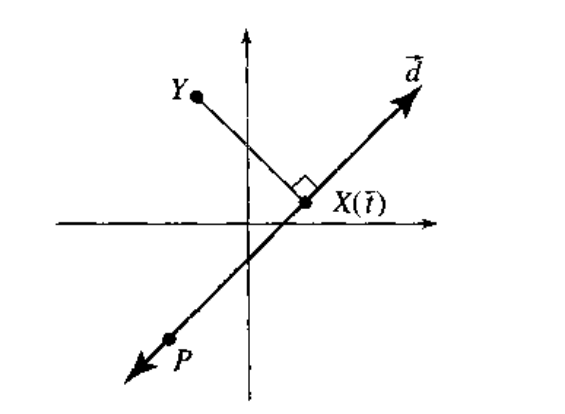
直线 L 的参数形式为

$ X(t) = P + t\overrightarrow{d}  $  // 式1

 

1. 先求点在直线上的投影点  X(t)；

2. 再求点 Y 到 X(t) 的距离，即可求得点到直线的距离；

3. 要求 X(t) 就是要求参数 t

 

向量 Y - X(t) 必然垂直于直线方向，因此

$ 0 = \overrightarrow{d} \cdot (Y - X(t)) $ // 式2

式1带入到式2

$ 0 = \overrightarrow{d} \cdot (Y - P - t\overrightarrow{d} ) =\overrightarrow{d} \cdot (Y - P) - t\left \| \overrightarrow{d}  \right \| ^{2}   $

变换之后可得

$ t = \frac{\overrightarrow{d}\cdot (Y - P) }{\left \| \overrightarrow{d}  \right \| ^{2} }   $

Y ，P 都是已知点，直线方向向量 d 也是已知，即可求得 t，从而求得点 Y 在直线上的投影，从而求得点 Y 到直线的距离。

 

下面来看一下 Occ 的实现 

 

void Extrema_ExtPElC2d::Perform(const gp_Pnt2d&     P, 
  const gp_Lin2d&     L,
  const Standard_Real Tol,
  const Standard_Real Uinf, 
  const Standard_Real Usup)
{
  myDone = Standard_True;
  gp_Pnt2d OR, MyP;
  myNbExt = 0;

  gp_Vec2d V1 = gp_Vec2d(L.Direction());
  OR = L.Location();
  gp_Vec2d V(OR, P);
  Standard_Real Mydist = V1.Dot(V);
  if ((Mydist >= Uinf -Tol) && 
    (Mydist <= Usup+ Tol)){ 
      myNbExt = 1;
      MyP = OR.Translated(Mydist*V1);
      Extrema_POnCurv2d MyPOnCurve(Mydist, MyP);
      mySqDist[0] = P.SquareDistance(MyP);
      myPoint[0] = MyPOnCurve;
      myIsMin[0] = Standard_True;
  }
}

V1 是直线的方向向量，就是上面推导过程的 直线 d 方向；

OR 是直线的参数 t = 0 的点，V 是 OR 往 P点的向量，就是上面推导出来的 （Y - P）；

由于 V1 在这里是个单位向量，因此分母部分就是1，那么Mydist 就是上面推导过程的 t；

这里有一个步骤是要判断 Mydist 必须在 两个参数Uinf， Usup之间，才能有结果。

MyP 就是 Or 沿着 V1 方向移动 Mydist 参数长度，即为 P 在 直线 L 上的投影点。

 

需要特别注意：这个算法只有当 P 的投影点在 Umin，Usup参数范围内，才有结果。

如果是想求点在整条直线的距离，只需把参数范围传入负无穷到正无穷