ch02_Probability_Distributions

目录

• 基本介绍
• 二元binary变量
• 多项式multinomial变量
• 高斯Gaussian分布
  • 条件高斯分布
  • 边际高斯分布
  • 分块高斯Partitioned Gaussians
  • 高斯变量的贝叶斯定理
  • 高斯分布的最大似然
  • 最大似然的序列估计
  • 高斯分布的贝叶斯推断
  • 学生t分布Student’s t-distribution
  • 周期变量Periodic variables
  • 高斯混合分布Mixtures of Gaussians
• 指数族
• 代码实现
• 原书存疑的地方

基本介绍

• 这一章讨论的概率分布的一个作用就是给定一个有限观测集合\(\vec{x}_1,\vec{x}_2,...,\vec{x}_N\)建模随机变量\(\vec{x}\)的概率分布\(p(\vec{x})\)。假设数据点独立同分布，应该强调的是，密度估计问题从根本上是ill-posed，因为有无限多的概率分布可能导致given rise to观测到的有限数据集。确实任何在数据点\(\vec{x}_1,...,\vec{x}_N\)处是非零的分布\(p(\vec{x})\)都是潜在的candidate。选择适当分布的问题涉及到模型选择问题，该问题在第一章多项式曲线拟合的背景下已经遇到，这是模式识别中的一个中心问题
• 我们首先考虑离散随机变量的二项式binomial和多项式multinomial分布以及连续随机变量的高斯分布。这些是参数分布的具体例子。之所以称为参数分布是因为它们受少量可调参数的控制，例如高斯分布的均值和方差。为了将这样的模型应用到密度估计问题，需要一个给定一个观测到的数据集确定合适参数值的过程。在一个频率者的解法treatment里，通过优化某个标准criterion如似然函数选择具体的参数值。相反，在一个贝叶斯解法里，引入参数的先验分布然后使用贝叶斯定理来计算对应的后验分布(给定观测数据)
• 共轭conjugate先验将起重要作用，使得后验分布的函数形式与先验一样。因此导致一个更简化的贝叶斯分析。例如：多项式分布参数的共轭先验是狄利克雷Dirichlet分布，高斯分布的均值的共轭先验是另一个高斯分布。所有这些分布都是指数分布族exponential family of distributions的例子，指数分布族拥有大量重要属性
• 参数方法的一个限制是它假设分布的一个具体函数形式，结果表明这可能不适合特定应用。另一个方法是则是无参nonparametric密度估计方法，分布的形式通常依赖于数据集的大小。这样的模型仍旧包含参数，但是这些参数控制着模型的复杂度而非分布的形式。三种无参方法：分别基于直方图histograms、最近邻nearest-neighbours和核kernels

二元binary变量

• 考虑一个单独的二元随机变量\(x\in \{0,1\}\)，例如，x可描述掷硬币flipping a coin的结果，x=1表示“头heads”，x=0表示“尾tails”。我们可以想象这是枚损坏damaged的硬币，因此头部落地的概率不一定与尾部相同。x=1的概率可用参数\(\mu\)表示：\(p(x=1|\mu)=\mu ,0\le \mu \le 1\)，\(p(x=0|\mu)=1-\mu\)。因此x上的概率分布可被写成：\(Bern(x|\mu)=\mu^x(1-\mu)^{1-x}\)，称作贝努利Bernoulli分布，该分布是标准化的且其均值和方差为\(E[x]=\mu,var[x]=\mu(1-\mu)\)
• 假设有一个数据集\(D=\{x_1,...,x_N\}\)(x的观测值)，可以创建似然函数，是\(\mu\)的函数(基于观测是从\(p(x|\mu)\)中独立获得的假设)：\(p(D|\mu)=\prod_{n=1}^Np(x_n|\mu)=\prod_{n=1}^N\mu^{x_n}(1-\mu)^{1-x_n}\)。在频率者设置下，可通过最大化似然函数估计一个\(\mu\)值，或等价地通过最大化似然的对数。在贝努利分布情况下，对数似然函数为\(logp(D|\mu)=\sum_{n=1}^Np(x_n|\mu)=\sum_{n=1}^N\{x_nln\mu+(1-x_n)ln(1-\mu)\}\)。对数似然函数只通过\(\sum_nx_n\)取决于\(x_n\)的N个观测。这个和提供了在这个分布下数据的充分统计量sufficient statistic的一个例子。关于\(\mu\)求导，可得到\(\mu\)的最大似然值\(\mu_{ML}=\frac{1}{N}\sum_{n=1}^Nx_n\)，称作样本均值。将x=1(头)的观测数设为m，则\(\mu_{ML}=\frac{m}{N}\)。因此，在这个最大似然框架下，头部落地的概率由数据集中头部观测的分数给出
• 现假设掷一枚硬币3次，且3次观测到头。那么N=m=3，\(\mu_{ML}=1\)。在这种情况下，最大似然结果会预测所有未来的观测都是头。常识common sense告诉我们这不合理，事实上这是与最大似然相关的过拟合的一个极端例子。引入\(\mu\)的先验分布得到更合理的结论
• 给定数据集的大小N，也可计算出x=1的观测数m的分布，称作二项binomial分布。从\(p(D|\mu)\)可看出，该分布与\(\mu^{m}(1-\mu)^{N-m}\)成比例。为了得到标准化系数，我们注意到，在N次掷硬币中，我们必须将所有可能获得m个头的方法加起来，所以二项分布为：\(Bin(m|N,\mu)=\begin{pmatrix} N \\ m \\ \end{pmatrix}\mu^{m}(1-\mu)^{N-m}\)，\(\begin{pmatrix} N \\ m \\ \end{pmatrix}=\frac{N!}{(N-m)!m!}\)表示从N个相同的物体中选择m个物体的方法数。对于独立事件，和的均值等于均值的和，和的方差等于方差的和。\(m=x_1+...+x_N\)，每个观测的均值和方差为\(E[x]=\mu,var[x]=\mu(1-\mu)\)，所以\(E[m]=\sum_{m=0}^NmBin(m|N,\mu)=N\mu,var[m]=\sum_{m=0}^N(m-E[m])^2Bin(m|N,\mu)=N\mu(1-\mu)\)
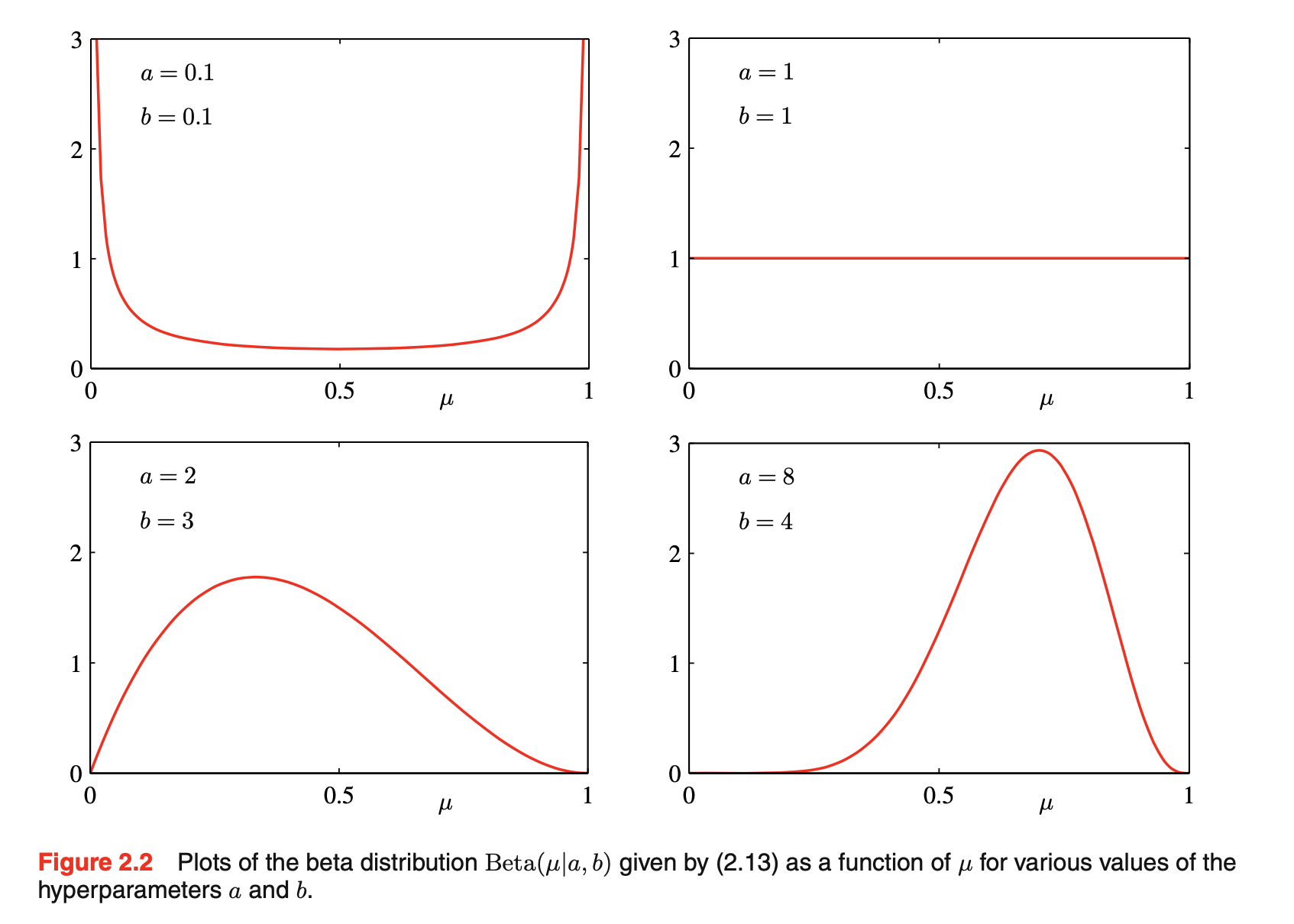
• 贝塔beta分布：为了发展一个贝叶斯解法，需要引入一个先验分布\(p(\mu)\)。这里我们考虑一种先验分布形式，它有一个简单的解释和一些有用的分析属性。为了motivate这个先验，我们注意到似然函数具有因子\(\mu^{x}(1-\mu)^{1-x}\)的乘积形式。若选择一个先验，它与\(\mu\)和\(1-\mu\)的幂成比例，那么后验分布与先验分布和似然函数的乘积成比例则具有和先验分布一样的函数形式，这种属性称作共轭conjugacy。因此选择一个先验称作贝塔分布：\(Beta(\mu|a,b)=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\mu^{a-1}(1-\mu)^{b-1}\)，\(\Gamma(x)=\int_0^{\infty}u^{x-1}e^{-u}du\)是伽马函数。上式的系数确保贝塔分布被标准化：\(\int_{0}^1Beta(\mu|a,b)d\mu=1\)。贝塔分布的均值和方差为：\(E[\mu]=\frac{a}{a+b},var[\mu]=\frac{ab}{(a+b)^2(a+b+1)}\)，参数a和b称作超参数，因为它们控制参数的分布。下图是贝塔分布。\(\mu\)的后验分布：将贝塔先验和二项式似然函数相乘并标准化，只保持依赖于\(\mu\)的因子：\(p(\mu|m,l,a,b)\propto \mu^{m+a-1}(1-\mu)^{l+b-1},l=N-m\)，有和先验分布一致的\(\mu\)的函数依赖，反映先验关于似然函数的共轭属性。确实，它是另一个贝塔分布，它的标准化系数可对比贝塔先验获得：\(p(\mu|m,l,a,b)=\frac{\Gamma(m+a+l+b)}{\Gamma(m+a)\Gamma(l+b)}\mu^{m+a-1}(1-\mu)^{l+b-1}\)。观测一个有m个x=1的观测和l个x=0观测的数据集的效果：从先验到后验，以m增加a值，以l增加b值。将先验中的超参数a和b解释成一个观测x = 1和x = 0的有效数目effective number of observations，a和b不需要是整数。如果随后观测到额外的数据，后验分布会和先验一样表现。想象一次只进行一次观测，每次观测后，通过乘以新观测的似然函数，更新当前的后验分布。然后标准化，得到新的修正的后验分布。在每个阶段，后验是个贝塔分布，由参数a和b给出的x=1和x=0的观测值的总数(包括先验和实际)。包含一个额外的x=1的观测只要对应于以1增加a值，然而x=0的一个观测则以1增加b。当我们采纳一个贝叶斯观点，这个序列sequential学习方法就会很自然地产生。它独立于先验的选择和似然函数的选择，仅依赖于独立同分布i.i.d.数据的假设。序列方法一次利用一个观测或一小批，然后在下一次观测被使用前抛弃它们。例如，它们可以用于实时学习场景中，在实时学习场景中，稳定的数据流将要到达，并且必须在看到所有数据之前进行预测。因为它们不需要将整个数据集存储或加载到内存中，所以序列方法对于大型数据集也很有用。最大似然方法也可以被转换成cast一个序列框架
  
  • 如果我们的目标是尽可能预测好下一次实验的结果，那么我们必须计算给定观测数据集D，x的预测分布。从概率的求和和乘积规则可得：\(p(x=1|D)=\int_0^1p(x=1|\mu)p(\mu|D)d\mu=\int_0^1\mu p(\mu|D)d\mu=E[\mu|D]\)，使用贝塔后验分布的结果以及贝塔分布的均值，可得: \(p(x=1|D)=\frac{m+a}{m+a+l+b}\)。简单解释为观测的总分数(对应于x=1，包括真实观测和虚拟fictitious先验观测)。在一个无限大数据下，\(m,l\to \infty\)，reduce to退化成最大似然结果。在一个无限大数据集下，贝叶斯和最大似然结果会是一致的agree，这是非常一般的属性。对于一个有限数据集，\(\mu\)的后验均值总是存在于先验均值和\(\mu\)的最大似然估计(对应于事件的相对relative频率)之间。从上图可见，随着观测数的增加，后验分布变得更加尖锐sharply peaked，这也可从贝塔分布的方差看出(当\(a\to \infty\)或\(b\to \infty\)方差变成0)。我们想知道是否这是贝叶斯学习的一个一般属性：当我们观测到越来越多的数据，后验分布所代表的不确定性将稳步降低。为了解决这个问题，我们可对贝叶斯学习采取一种频率者观点，并表明，平均而言，这样的属性确实成立

多项式multinomial变量

• 二元变量可用于描述可以取两个可能值之一的量，但我们经常会遇到具有K种可能互斥状态之一的离散变量。虽然有各种方法来表达这样的变量，但一个特别方便的表示是1-of-K scheme(变量由一个K维向量\(\vec{x}\)表示，其中某个元素\(x_k=1\)，其余元素为0)。例如有一个变量，可取K=6个状态，且该变量的一个特定的观测碰巧是\(x_3=1\)的状态，那么\(\vec{x}=(0,0,1,0,0,0)^T\)。这样的变量满足\(\sum_{k=1}^{K}x_k=1\)。将\(x_k=1\)的概率记作参数\(\mu_k\)，那么\(\vec{x}\)的分布：\(p(\vec{x}|\vec{\mu})=\prod_{k=1}^K\mu_k^{x_k},\vec{\mu}=(\mu_1,...,\mu_K)^T,\mu_k\ge 0,\sum_k\mu_k=1\)。可被当作是贝努利分布的一个推广(超过两个输出)。分布是标准化的：\(\sum_{\vec{x}}p(\vec{x}|\vec{\mu})=\sum_{k=1}^K\mu_k=1\)。\(E[\vec{x}|\vec{\mu}]=\sum_{\vec{x}}p(\vec{x}|\vec{\mu})\vec{x}=(\mu_1,...,\mu_K)^T=\vec{\mu}\)
• 现在考虑一个有N个独立观测\(\vec{x}_1,...,\vec{x}_N\)数据集D，对应的似然函数：\(p(D|\vec{\mu})=\prod_{n=1}^N\prod_{k=1}^K\mu_k^{x_{nk}}=\prod_{k=1}^K\mu_k^{(\sum_nx_{nk})}=\prod_{k=1}^K\mu_k^{m_k}\)。似然函数只通过K个量\(m_k=\sum_nx_{nk}\)(表示\(x_k=1\)的观测数，称作这个分布的充分统计量)依赖于N个数据点。为了找到\(\vec{\mu}\)的最大似然解，关于\(\mu_k\)最大化\(lnp(D|\vec{\mu})\)(考虑\(\mu_k\)必须加和为1的约束): \(\sum_{k=1}^Km_kln\mu_k+\lambda(\sum_{k=1}^K\mu_k-1)\) 。让上式关于\(\mu_k\)的导数等于0，得到\(\mu_k=-m_k/\lambda\)。将该式代到约束中可求出\(\lambda = -N\)。因此得到最大似然解：\(\mu_k^{ML}=\frac{m_k}{N}\)。考虑以参数\(\vec{\mu}\)和观测总数N为条件的\(m_1,..,m_K\)的联合分布，\(Mult(m_1,m_2,..,m_K|\vec{\mu},N)=\begin{pmatrix} N \\ m_1m_2..m_K \\ \end{pmatrix}\prod_{k=1}^K\mu_k^{m_k}\)，称作多项式分布。标准化系数是划分N个对象到K族(大小为\(m_1,..,m_K\))的方法数：\(\begin{pmatrix} N \\ m_1m_2..m_K \\ \end{pmatrix}=\frac{N!}{m_1!m_2!...m_K!}\)，约束: \(\sum_{k=1}^Km_k=N\)
• 狄利克雷dirichlet分布：引入参数\(\{\mu_k\}\)的一类先验分布。通过检查多项式分布的形式，可以给出共轭先验：\(p(\vec{\mu}|\vec{\alpha})\propto \prod_{k=1}^K\mu_k^{\alpha_k-1},0\le \mu_k\le 1,\sum_k\mu_k=1\)。由于加和约束，在\(\{\mu_k\}\)空间上的分布被限制confined成维数为K-1的单纯形simplex，如下图所示。该先验分布标准化后的形式：\(Dir(\vec{\mu}|\vec{\alpha})=\frac{\Gamma(\alpha_0)}{\Gamma(\alpha_1)...\Gamma(\alpha_K)}\prod_{k=1}^K\mu_k^{\alpha_k-1},\alpha_0=\sum_{k=1}^K\alpha_k\)，称作狄利克雷分布。先验乘以似然函数得到后验分布：\(p(\vec{\mu}|D,\vec{\alpha})\propto p(D|\vec{\mu})p(\vec{\mu}|\vec{\alpha})\propto \prod_{k=1}^K\mu_k^{\alpha_k+m_k-1}\)，后验分布也是一个狄利克雷分布形式，说明狄利克雷确实是多项式的一个共轭先验。对比先验可确定标准化系数：\(p(\vec{\mu}|D,\vec{\alpha})=Dir(\vec{\mu}|\vec{\alpha}+\vec{m})=\frac{\Gamma(\alpha_0+N)}{\Gamma(\alpha_1+m_1)...\Gamma(\alpha_K+m_K)}\prod_{k=1}^K\mu_k^{\alpha_k+m_k-1}\)，将\(\alpha_k\)解释成\(x_k=1\)观测的有效数目。两状态的量要么可表示为二元变量并用二项分布建模，要么表示为1-of-2变量并用K=2的多项式分布建模
  

高斯Gaussian分布

• 高斯分布(正态)是个被广泛使用的连续变量分布的模型。在单变量x的情况下，高斯分布可写作：\(N(x|\mu,\sigma^2)=\frac{1}{(2\pi \sigma^2)^{1/2}}exp\{-\frac{1}{2\sigma^2}(x-\mu)^2\}\)。对于一个D维向量\(\vec{x}\)，多变量高斯分布写作：\(N(\vec{x}|\vec{\mu},\Sigma)=\frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma|^{1/2}}exp\{-\frac{1}{2}(\vec{x}-\vec{\mu})^T\Sigma^{-1}(\vec{x}-\vec{\mu})\}\)。例如，对于单个实变量，最大化熵的分布是高斯，这个属性也适用于多变量高斯
• 高斯分布出现的另一个情况是当我们考虑多个随机变量之和时。中心极限定理central limit theorem(due to Laplace)告诉我们：在某些温和的条件下，一组随机变量的和，其本身就是一个随机变量，其分布随着和中项数的增加而变得越来越高斯。考虑N个变量\(x_1,...,x_N\)，每一个是[0,1]上的均匀分布。然后考虑均值\((x_1+...+x_N)/N\)的分布。对于大的N，这个分布倾向于高斯。实际上，随着N的增加，收敛到高斯分布的速度会非常快。如二项分布(被随机二元变量x的N个观测的和定义的m上的一个分布)当\(N\to \infty\)时会倾向于高斯
• 考虑高斯分布的几何形式:
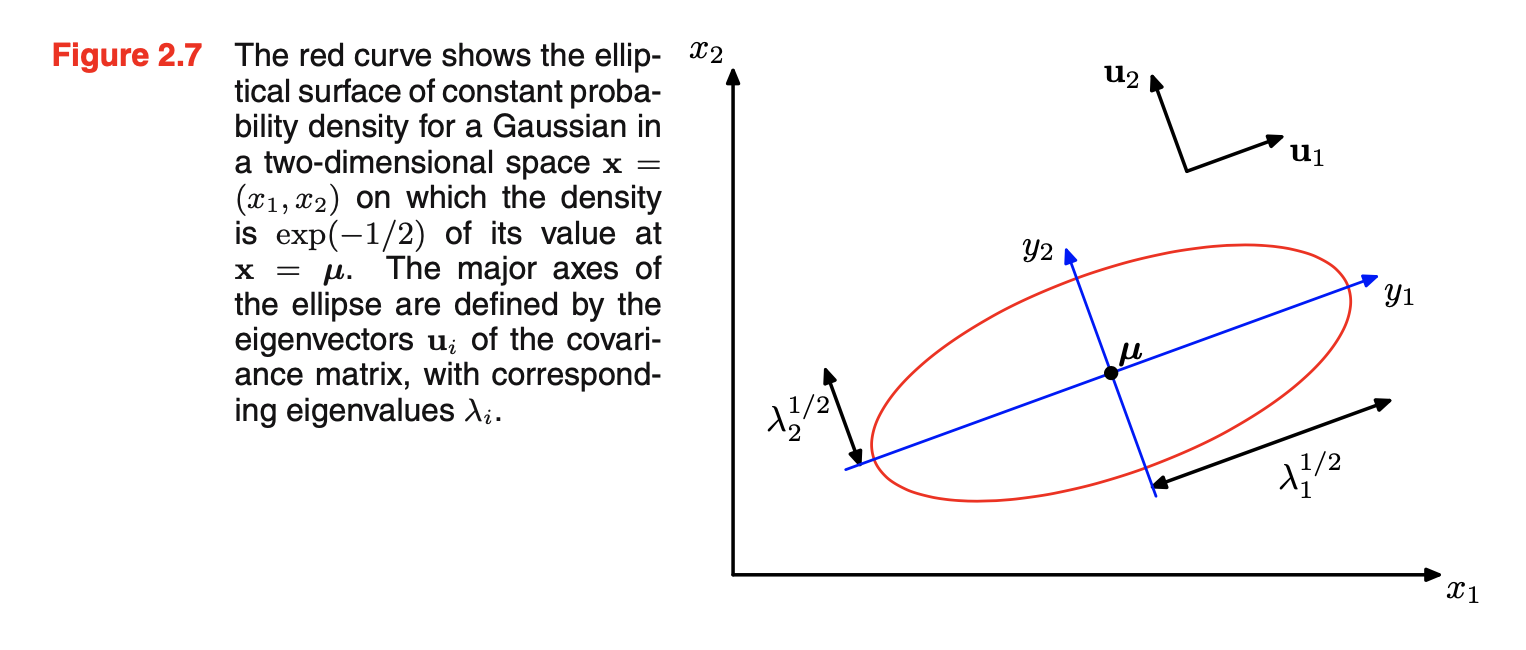
  • 高斯的函数依赖\(\vec{x}\)是通过二次型：\(\Delta^2=(\vec{x}-\vec{\mu})^T\Sigma^{-1}(\vec{x}-\vec{\mu})\)。量\(\Delta\)被称作从\(\vec{\mu}\)到\(\vec{x}\)的Mahalanobis距离。当\(\Sigma\)是单位矩阵时则退化成欧式Euclidean距离。在这个二次型为常数的\(\vec{x}\)空间曲面上，高斯分布是常数。一般\(\Sigma\)是对称的，因为任何反对称antisymmetric的成分会从指数中消失。考虑\(\Sigma\)协方差矩阵的特征向量等式：\(\Sigma\vec{u}_i=\lambda_i\vec{u}_i,i=1,...,D\)。可引入一个新的坐标系统\(\{y_i\}\)，由标准正交向量\(\vec{u}_i\)定义，如下图所示。
    
  • 若要使高斯分布被良好定义，则有必要使所有特征值\(\lambda_i\)严格为正，否则分布就无法标准化。特征值严格为正的矩阵称为正定矩阵positive definite。若高斯分布的一个或多个特征值为0，那么分布是奇异的singular，并被限制在一个低维的子空间中。若所有特征值都是非负，则协方差矩阵是半正定positive semidefinite
  • 考虑高斯分布在新坐标系中的形式(由\(y_i\)定义)：\(p(\vec{y})=p(\vec{x})|J|=\prod_{j=1}^D\frac{1}{(2\pi \lambda_j)^{1/2}}exp\{-\frac{y_j^2}{2\lambda_j}\}\)，D个独立单变量高斯分布单乘积。特征向量定义了一组新的平移的和旋转的坐标，联合概率分布将其分解成独立分布的乘积
  • \(E[\vec{x}]=\vec{\mu},E[\vec{x}\vec{x}^T]=\Sigma+\vec{\mu}\vec{\mu}^T,cov[\vec{x}]=\Sigma\)
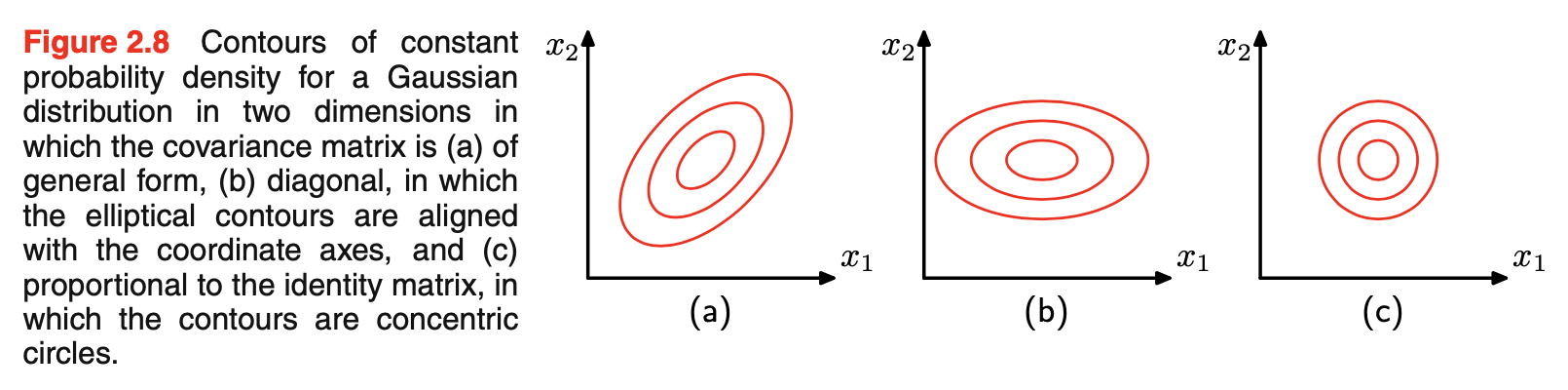
• 尽管高斯分布被广泛用作密度模型，但它有一些显著的限制。考虑分布中自由参数数目，一般对称协方差矩阵\(\Sigma\)会有D(D+1)/2个独立参数，\(\vec{\mu}\)中另有D个独立参数，总共有D(D+3)/2个参数。对于大的D，参数总数会与D呈二次增长quadratically。操作和逆大型矩阵会变得困难prohibitive。一个解决方法是使用协方差矩阵的限制形式restricted forms of the covariance matrix。若考虑协方差是对角的，那么\(\Sigma=diag(\sigma_i^2)\)，这样一共有2D个参数，相应的常量密度等值线contours由轴对齐axis-aligned的椭球体ellipsoids给出。进一步限制协方差矩阵与单位矩阵成比例，\(\Sigma=\sigma^2I\)，称作各项同性isotropic协方差，有D + 1个独立参数，常量密度的球面spherical surfaces of constant density。如下图所示。但这样的方法限制分布中自由度的数目，虽使得协方差矩阵的逆更快操作，但十分限制概率密度的形式，并限制它捕获数据中有趣关联correlations的能力。高斯分布更进一步限制是其本质上是单峰的unimodal(即有单一的最大值)，所以不能提供多峰multimodal分布的良好估计。因此，高斯分布在参数过多的意义上可能过于灵活，同时在其能够充分表示的分布范围上也过于有限。引入隐含变量latent variables/hidden variables/unobserved variables，可以解决这两个问题。特别的，通过引入导致高斯混合的离散隐含变量，得到了丰富的多峰分布族。类似地，连续隐含变量的引入导致模型中自由参数的数量可以独立于数据空间的维数D进行控制，同时仍然允许模型捕获数据集中的主要相关性。事实上，这两种方法可以结合并进一步扩展，以得到一组非常丰富的层次模型，这些模型可以适应广泛的实际应用。例如，马尔可夫随机场Markov random field的高斯分布是像素强度在联合空间上的高斯分布，它被广泛用作图像的概率模型，但通过施加反映像素空间组织的相当大的结构而变得易于处理。类似地，用于为追踪等应用建立时间序列数据模型的线性动力系统linear dynamical system，也是潜在大量观测变量和隐含变量上的联合高斯分布，并且由于分布上施加的结构，同样是可处理的。表达这样复杂分布的形式和属性的有力框架是概率图模型probabilistic graphical models
  

条件高斯分布

• 多变量高斯分布的一个重要性质是，如果两组变量同时为高斯分布，则一组变量的条件分布(以另一组为条件)还是高斯分布。类似地，任一组的边际分布也是高斯分布
• 假设\(\vec{x}\)是D维向量，具有高斯分布\(N(\vec{x}|\vec{\mu},\Sigma)\)，划分\(\vec{x}\)成两个不相交disjoint的子集\(\vec{x}_a\)和\(\vec{x}_b\)，使得\(\vec{x}_a\)成为\(\vec{x}\)的前m个成分，\(\vec{x}_b\)对应后D-m个，即\(\vec{x}=\begin{pmatrix}\vec{x}_a\\\vec{x}_b\end{pmatrix}\)，同时也定义均值向量\(\vec{\mu}=\begin{pmatrix}\vec{\mu}_a\\\vec{\mu}_b\end{pmatrix}\)，协方差矩阵\(\Sigma=\begin{pmatrix}\Sigma_{aa} & \Sigma_{ab}\\\Sigma_{ba} & \Sigma_{bb}\end{pmatrix}\)，precision矩阵\(\Lambda=\begin{pmatrix}\Lambda_{aa} & \Lambda_{ab}\\\Lambda_{ba} & \Lambda_{bb}\end{pmatrix}\)
• 为条件分布\(p(\vec{x}_a|\vec{x}_b)\)找一个表达式：其均值为\(\vec{\mu}_{a|b}=\vec{\mu}_a-\Lambda_{aa}^{-1}\Lambda_{ab}(\vec{x}_b-\vec{\mu}_b)\)，协方差为\(\Sigma_{a|b}=\Lambda^{-1}_{aa}\)，这是用分块partitioned precision矩阵表示的，也可以用分块协方差矩阵表示：\(\vec{\mu}_{a|b}=\vec{\mu}_a+\Sigma_{ab}\Sigma_{bb}^{-1}(\vec{x}_b-\vec{\mu}_b)\)，\(\Sigma_{a|b}=\Sigma_{aa}-\Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba}\)。当用分块协方差矩阵表示时，\(\vec{\mu}_{a|b}\)是\(\vec{x}_b\)的线性函数，\(\Sigma_{a|b}\)独立于\(\vec{x}_a\)，这是线性高斯linear-Gaussian模型的一个例子

边际高斯分布

• 若一个联合分布\(p(\vec{x}_a,\vec{x}_b)\)是高斯，则条件分布\(p(\vec{x}_a|\vec{x}_b)\)也会是高斯。边际分布\(p(\vec{x}_a)=\int p(p(\vec{x}_a,p(\vec{x}_b)dp(\vec{x}_b\)也是高斯。有效计算这个分布的策略是关注联合分布指数中的二次型，因此去识别边际分布\(p(\vec{x}_a)\)的均值和协方差
• 联合分布的二次型可用分块precison矩阵表示。边际分布\(p(\vec{x}_a)\)均值为\(\vec{\mu}_a\)，协方差为\(\Sigma_a=(\Lambda_{aa}-\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1}\)，这是用分块partitioned precision矩阵表示的，也可以用分块协方差矩阵表示：均值仍为\(\vec{\mu}_a\)，协方差为\(\Sigma_{aa}\)。对于一个边际分布，均值和协方差用分块协方差矩阵表示最简单，而对于条件分布，用分块precision矩阵表示更简单

分块高斯Partitioned Gaussians

• 给定联合高斯分布\(N(\vec{x}|\vec{\mu},\Sigma)\)，且\(\Lambda=\Sigma^{-1}\)，\(\vec{x}=\begin{pmatrix}\vec{x}_a\\\vec{x}_b\end{pmatrix}\)，\(\vec{\mu}=\begin{pmatrix}\vec{\mu}_a\\\vec{\mu}_b\end{pmatrix}\)，\(\Sigma=\begin{pmatrix}\Sigma_{aa} & \Sigma_{ab}\\\Sigma_{ba} & \Sigma_{bb}\end{pmatrix}\)，\(\Lambda=\begin{pmatrix}\Lambda_{aa} & \Lambda_{ab}\\\Lambda_{ba} & \Lambda_{bb}\end{pmatrix}\)。条件分布为\(p(\vec{x}_a|\vec{x}_b)=N(\vec{x}_a|\vec{\mu}_{a|b},\Lambda^{-1}_{aa})\)，\(\vec{\mu}_{a|b}=\vec{\mu}_a-\Lambda_{aa}^{-1}\Lambda_{ab}(\vec{x}_b-\vec{\mu}_b)\)。边际分布为\(p(\vec{x}_a)=N(\vec{x}_a|\vec{\mu}_a,\Sigma_{aa})\)

高斯变量的贝叶斯定理

• 边际和条件高斯：\(p(\vec{x})=N(\vec{x}|\vec{\mu},\Lambda^{-1}),p(\vec{y}|\vec{x})=N(\vec{y}|A\vec{x}+\vec{b},L^{-1}),p(\vec{y})=N(\vec{y}|A\vec{\mu}+\vec{b},L^{-1}+A\Lambda^{-1}A^T),p(\vec{x}|\vec{y})=N(\vec{x}|\Sigma\{A^TL(\vec{y}-\vec{b})+\Lambda\vec{\mu}\},\Sigma),\Sigma=(\Lambda+A^TLA)^{-1}\)

高斯分布的最大似然

• 对数似然函数：\(lnp(X|\vec{\mu},\Sigma)=-\frac{ND}{2}ln(2\pi)-\frac{N}{2}ln|\Sigma|-\frac{1}{2}\sum_{n=1}^{N}(\vec{x}_n-\vec{\mu})^T\Sigma^{-1}(\vec{x}_n-\vec{\mu})\)
• 似然函数只通过两个量依赖数据集，即\(\sum_{n=1}^{N}\vec{x}_n,\sum_{n=1}^{N}\vec{x}_n\vec{x}_n^T\)，称作高斯分布的充分统计量
• 均值的最大似然解：\(\vec{\mu}=\frac{1}{N}\sum_{n=1}^{N}\vec{x}_n\)，协方差的最大似然解：\(\Sigma_{ML}=\frac{1}{N}\sum_{n=1}^{N}(\vec{x}_n-\vec{\mu}_{ML})(\vec{x}_n-\vec{\mu}_{ML})^T\)
• 在真实分布下计算最大似然解的期望：\(E[\vec{\mu}_{ML}]=\vec{\mu},E[\Sigma_{ML}]=\frac{N-1}{N}\Sigma\)。均值的最大似然估计的期望等于真实均值，但协方差的最大似然估计的期望小于真实值。因此它是有偏的。我们可以通过定义一个不同的估计器纠正这个bias，即\(\tilde{\Sigma}=\frac{1}{N-1}\sum_{n=1}^{N}(\vec{x}_n-\vec{\mu}_{ML})(\vec{x}_n-\vec{\mu}_{ML})^T\)

最大似然的序列估计

• 序列方法允许一次处理一个数据点然后抛弃，对于在线应用和大数据集的批处理不可行时是重要的
• 均值的最大似然估计可分解为: \(\vec{\mu}_{ML}=\vec{\mu}_{ML}^{(N)}=\frac{1}{N}\sum_{n=1}^{N}\vec{x}_n=\frac{1}{N}\vec{x}_N+\frac{1}{N}\sum_{n=1}^{N-1}\vec{x}_n=\frac{1}{N}\vec{x}_N+\frac{N-1}{N}\vec{\mu}_{ML}^{(N-1)}=\vec{\mu}_{ML}^{(N-1)}+\frac{1}{N}(\vec{x}_N-\vec{\mu}_{ML}^{(N-1)})\)。当N增大时，来自连续数据点的贡献会变小
• 序列学习的一般形式: Robbins-Monro算法
  • 考虑一对由联合分布\(p(z, \theta)\)控制的随机变量\(\theta\)和z，给定\(\theta\)的z的条件期望定义了一个确定性函数\(f(\theta)\)，即\(f(\theta)=E[z|\theta]=\int zp(z|\theta)dz\)，以这种方式定义的函数成为回归函数
    
  • 如果有\(\theta\)和z的大量观测，则可直接建模回归函数，并得到其根的估计；如果一次只能观测到一个z值，希望找到一个序列估计\(\theta^{*}\)的方法。如上图所示，Robbins-Monro算法给出了找到这种函数根\(\theta^{*}\)的一般序列过程：\(\theta^{(N)}=\theta^{(N-1)}+a_{N-1}z(\theta^{(N-1)})\)
  • 使用Robbins-Monro算法解决一般最大似然问题：\(E_{\vec{x}}[\frac{\partial}{\partial \theta}lnp(\vec{x}|\theta)]\)。找最大似然解对应于找回归函数的根。考虑高斯分布均值的序列估计，此时\(\theta^{(N)}\)是\(\mu_{ML}^{(N)}\)，\(z=\frac{\partial}{\partial \mu_{ML}}lnp(x|\mu_{ML},\sigma^2)=\frac{1}{\sigma^2}(x-\mu_{ML})\)，因此z的分布是均值为\(\mu-\mu_{ML}\)的高斯，如下图所示。
    

高斯分布的贝叶斯推断

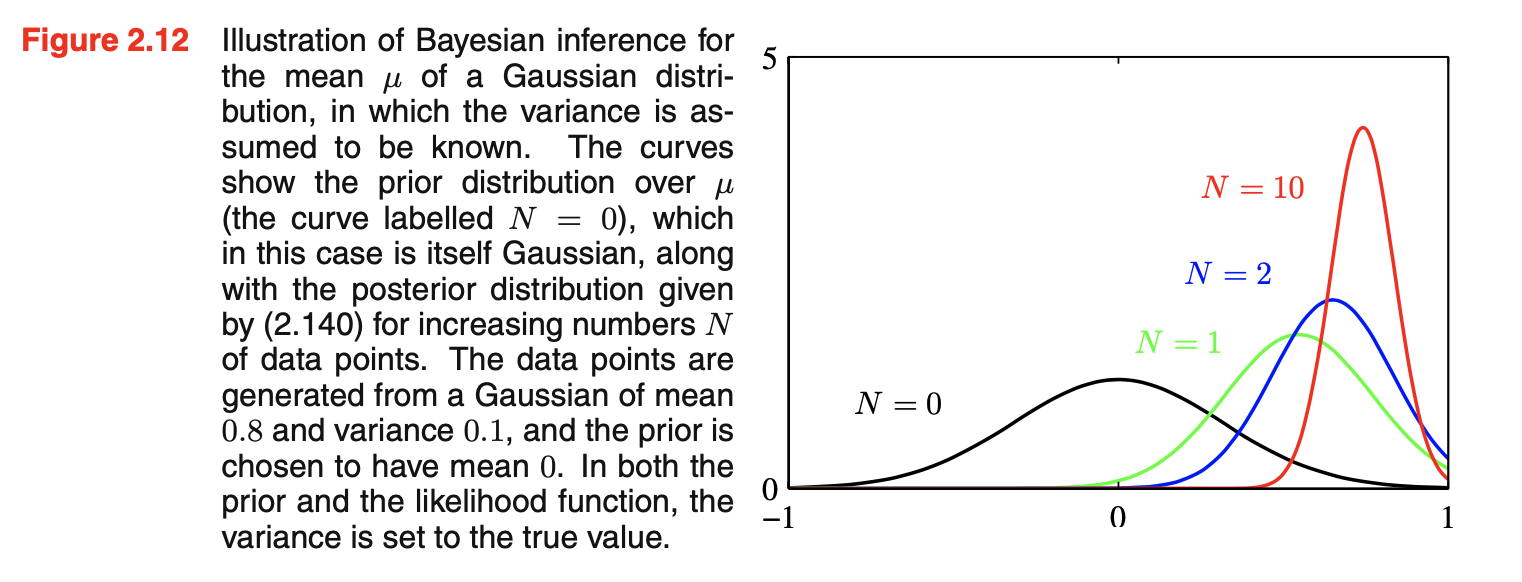
• 最大似然框架给出给出参数\(\vec{\mu}\)和\(\Sigma\)的点估计，现在通过引入参数的先验分布来介绍贝叶斯解法。下图是高斯分布均值的贝叶斯推断，假设方差已知。
  
• 贝叶斯解法可以非常自然得到推断问题的序列视角，假设观测数据是独立同分布
• 假设均值已知，推断方差：
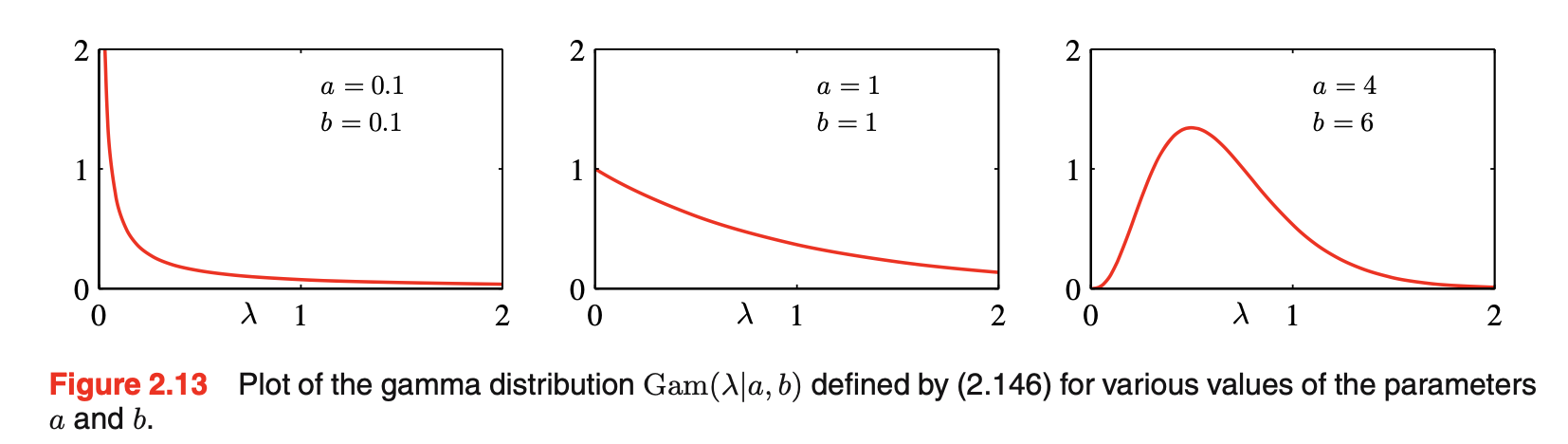
  • 确定似然函数的对应共轭先验是gamma分布：\(Gam(\lambda|a,b)=\frac{1}{\Gamma(a)}b^a\lambda^{a-1}exp\)，如下图所示：
    
  • gamma先验与狄利克雷先验类似，都是指数族的例子，将共轭先验解释成有效虚拟数据点是指数族分布的一般属性
• 假设均值和precision均未知：
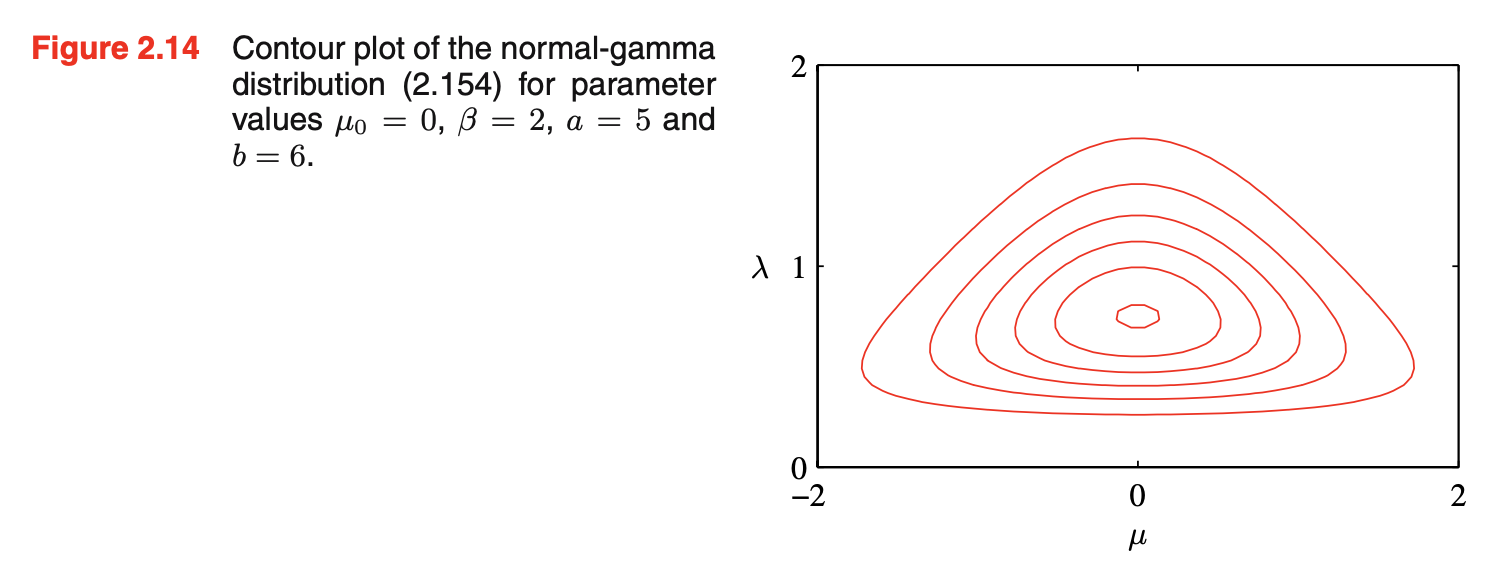
  • 确定先验分布\(p(\mu,\lambda)\)为normal-gamma或Gaussian-gamma分布，即\(p(\mu,\lambda)=p(\mu|\lambda)p(\lambda)\)。如下图所示。该分布不是简单地由一个\(\mu\)上的独立高斯先验和一个\(\lambda\)上的gamma先验乘积得到，因为\(\mu\)的precision是\(\lambda\)的一个线性函数；即使选择一个先验，其中\(\mu\)和\(\lambda\)是独立的，后验分布也会显示出\(\mu\)的precision和\(\lambda\)值的耦合
    
• 对于多变量高斯分布，假设precision未知，均值的共轭先验还是高斯分布；假设均值已知，precison矩阵\(\Lambda\)未知，则共轭先验为Wishart分布；也可在协方差矩阵上定义共轭先验，为逆Wishart分布；若均值和precision均未知，共轭先验为normal-Wishart或Gaussian-Wishart分布

学生t分布Student’s t-distribution

• 高斯分布的precision共轭先验是gamma分布
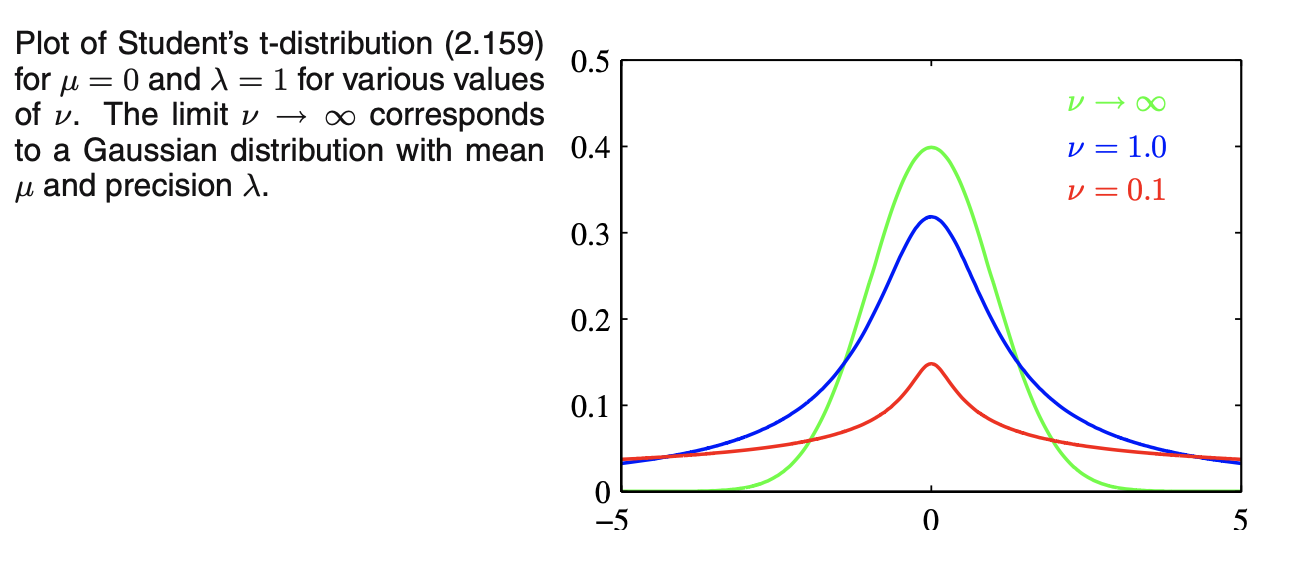
• 单变量高斯乘以gamma分布，并对precision积分，可得到x的边际分布\(p(x|\mu,a,b)\)，定义新参数\(\nu=2a,\lambda=a/b\)，则\(p(x|\mu,a,b)\)变成\(St(x|\mu,\lambda,\nu)\)，得到学生t分布，其中\(\lambda\)有时称作t分布的precision，尽管它一般不等于方差的倒数；\(\nu\)称作自由度degrees of freedom，它的影响见下图：当\(\nu=1\)时，t分布变成柯西分布Cauchy distribution，当\(\nu\to\infty\)时，t分布变成均值为\(\mu\)、precision为\(\lambda\)的高斯分布\(N(x|\mu,\lambda^{-1})\)
  
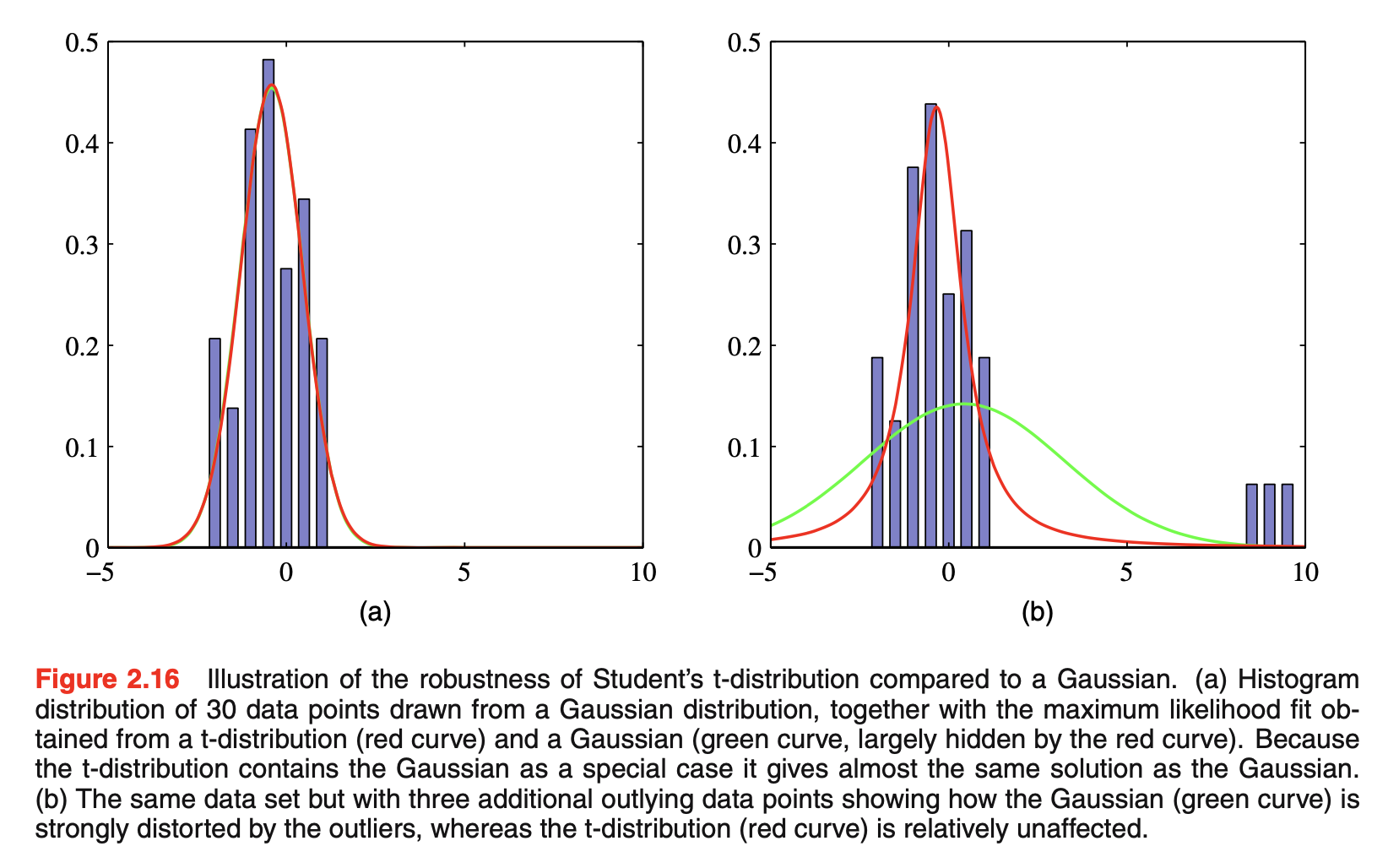
• t分布是通过将具有相同均值但不同精度的无穷多个高斯分布相加得到的，这可看成是一个高斯的无限混合infinite mixture of Gaussians(高斯混合Gaussian mixtures的结果一般是一个具有比高斯分布更长尾巴的分布，如上图所示)。这给了t分布一个重要属性称作鲁棒性robustness，指它对一些异常点outliers的出现比高斯分布更不敏感。t分布的鲁棒性如下图所示：其中t分布的最大似然解可用EM(expectation-maximization)算法
  
• 在实际应用中，异常点的出现可能是因为生成数据的过程对应于一个带有长尾heavy tail的分布，或者仅仅是由于错误标记的数据。鲁棒性也是回归问题的一个重要属性，但回归的最小二乘法least squares并不具有鲁棒性，因为它对应于(条件)高斯分布下的最大似然。在t分布等长尾分布的基础上建立回归模型，可得到了一个更健壮的模型
• 可推广到多变量t分布\(St(\vec{x}|\vec{\mu},\Lambda,\nu)\)

周期变量Periodic variables

• 尽管高斯分布本身和作为更复杂概率模型的构建块都具有重要的实际意义，但在某些情况下，它们不适合作为连续变量的密度模型。在实际应用中出现的一个重要情况是周期变量。
• 周期变量的一个例子是特定地理位置的风向。例如，我们可以测量若干天的风向值，并希望使用参数分布来总结这一点。另一个例子是日历时间，我们可能会对那些被认为是以24小时或一年为周期的量进行建模。这些量可以很方便地用角(极)坐标\(0\le\theta <2\pi\)来表示。
• 我们可能会倾向于选择某个方向作为原点来处理周期变量，然后应用常规分布，如高斯分布。然而，这种方法将产生强烈依赖于任意选择原点的结果。假设有两个观测处在\(\theta_1=1^{\circ}\)和\(\theta_2=359^{\circ}\)，使用标准单变量高斯分布来建模它们，如果选择原点在\(0^{\circ}\)，则这个数据集的样本均值为\(180^{\circ}\)，标准差为\(179^{\circ}\)。但如果选择原点在\(180^{\circ}\)，则均值为\(0^{\circ}\)，标准差为\(1^{\circ}\)。我们显然需要发展一种特殊的方法来处理周期变量
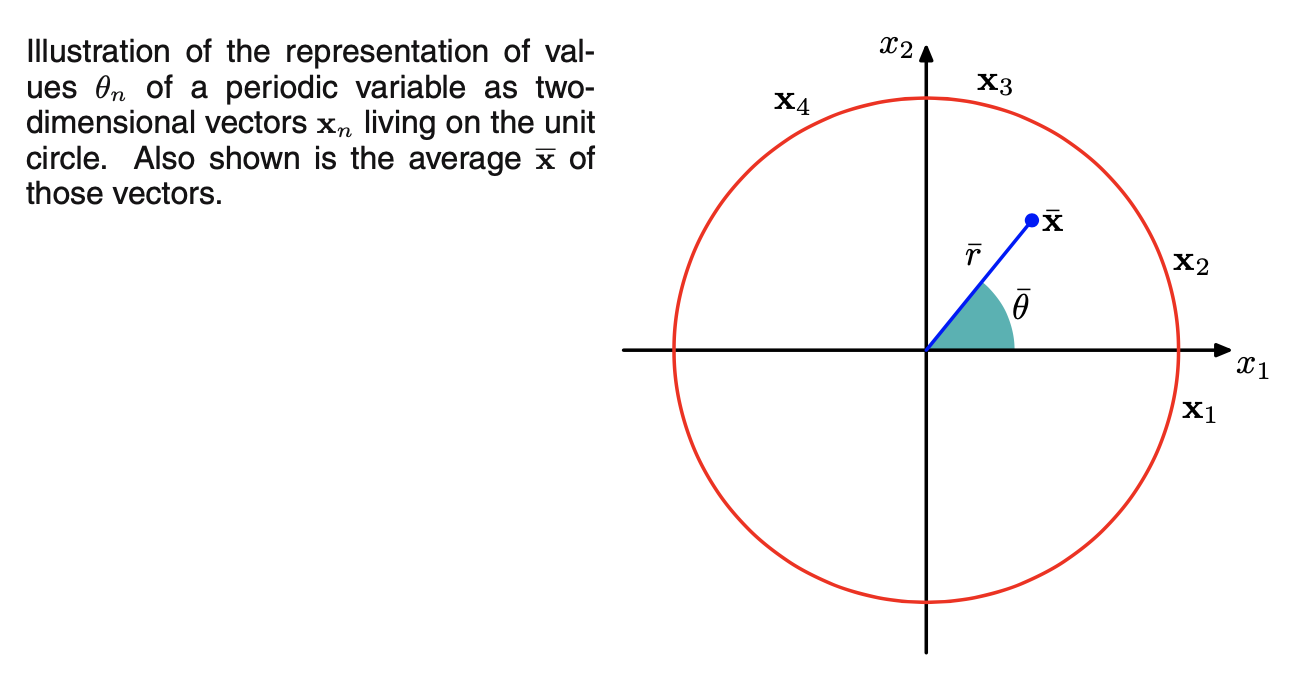
• 观测的简单平均是强坐标相关strongly coordinate dependent，为找到均值的不变测量，将观测看成是单位圆上的点，用二维单位向量描述，如下图所示：\(\bar{x}\)是\(\{x_n\}\)的均值。这个定义会确保均值的位置独立于极坐标系的原点。\(\bar{x}\)一般在单位圆内。
  
• 考虑一个称为von Mises分布的高斯分布的周期性推广。这里我们将把注意力限制在单变量分布上，尽管周期分布也可以在任意维的超球面上找到
  • 考虑具有周期为\(2\pi\)的分布\(p(\theta)\)，任何定义在\(\theta\)上的概率密度\(p(\theta)\)不仅需要非负、积分为1，还需要满足周期性。即
    \( \begin{cases} p(\theta)\ge 0 \\ \int_0^{2\pi}p(\theta)d\theta=1 \\ p(\theta+2\pi)= p(\theta) \\ \end{cases} \)
  • 可很容易得到一个类高斯Gaussian-like分布满足上述三个属性。如二维高斯分布\(p(\vec{x})\)，如下图所示：常数\(p(\vec{x})\)的轮廓contours是圆。现在假设我们考虑沿着一个固定半径的圆的分布值。然后通过构造，这个分布将是周期性的，尽管它不会被标准化
    
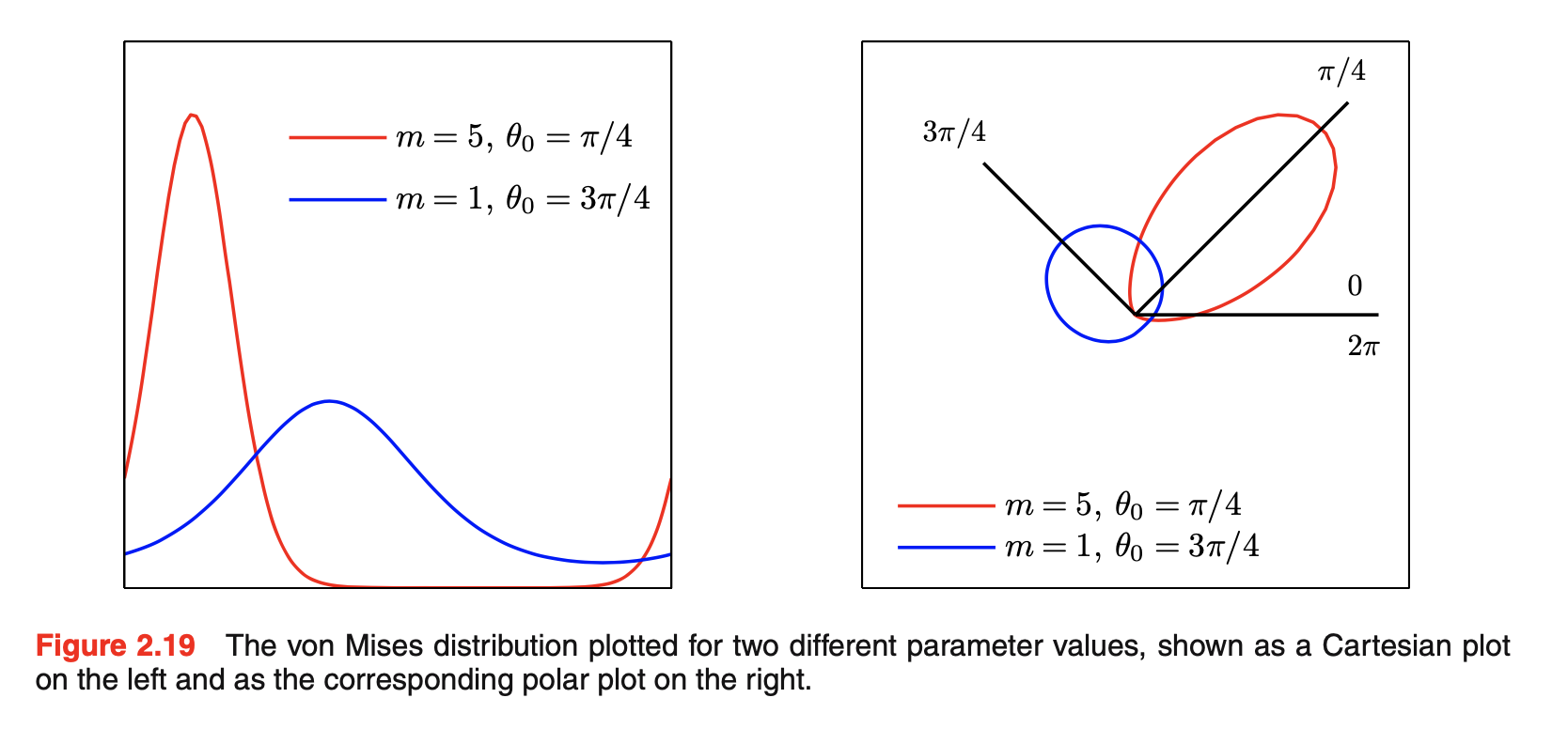
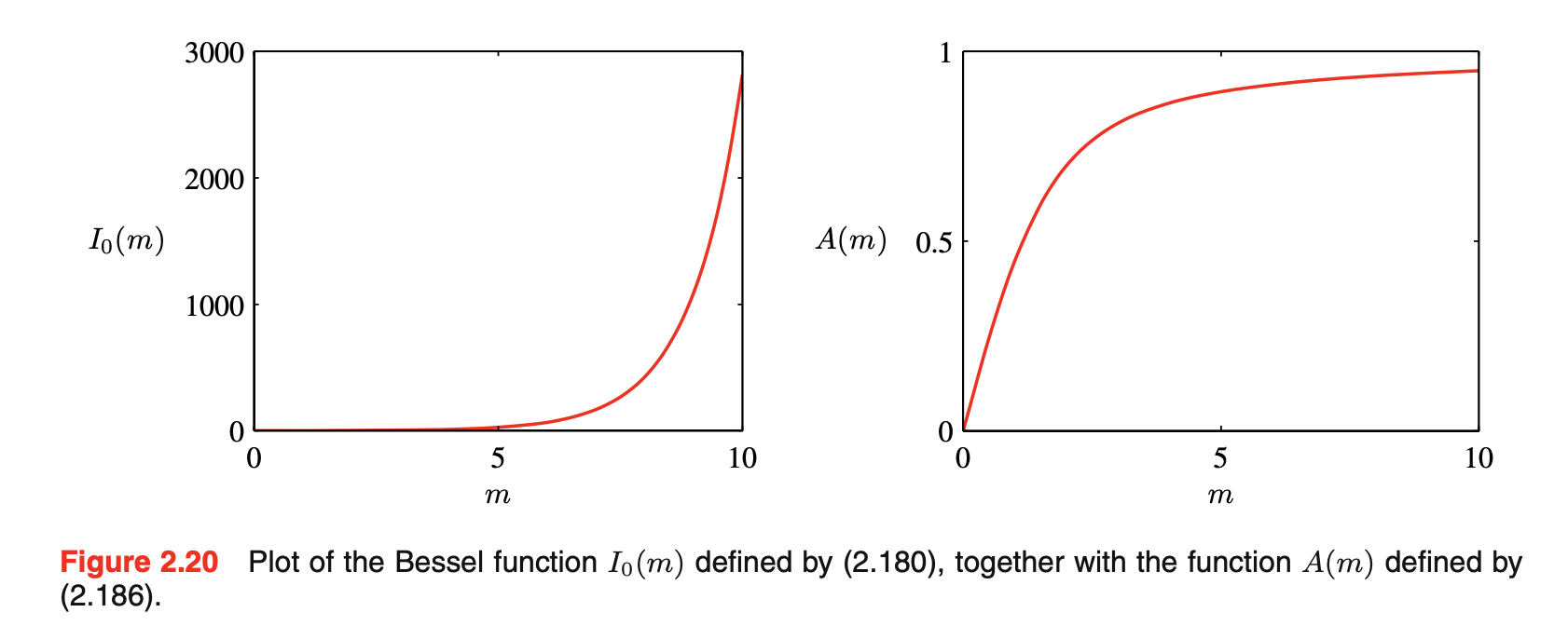
  • \(p(\theta|\theta_0,m)=\frac{1}{2\pi I_0(m)}exp\{mcos(\theta-\theta_0)\}\)称作von Mises分布，或circular normal，其中\(\theta_0\)对应于分布的均值，m为concentration parameter，类似于高斯分布的precision，\(I_0(m)\)是标准化系数，是zeroth-order Bessel function of the first kind，定义为\(I_0(m)=\frac{1}{2\pi}\int_0^{2\pi}exp\{mcos\theta\}d\theta\)。m越大，该分布会近似高斯分布。von Mises分布以及\(I_0(m)\)如下图所示：其中\(A(m)=\frac{I_1(m)}{I_0(m)},I^{'}_0(m)=I_1(m)\)
    
    
• 为了完整性，我们简要地提到了构造周期分布的一些替代技术。最简单的方法是使用观测值的直方图，其中角度坐标被划分为固定的bins。这有着简单和灵活的优点，但也有很大的局限性。另一种方法从欧几里德空间上的高斯分布开始，像von Mises分布，但是边缘化到单位圆上，而不是条件化。然而，这将导致更复杂的分布形式。最后，通过将宽度为\(2\pi\)的连续区间映射到周期变量\((0,2\pi)\)上，可将实数轴上的任何有效分布(如高斯分布)转化为周期分布，对应于将实轴“绕wrapping”在单位圆上。同样，得到的分布比von Mises分布更难处理
• von Mises分布的一个局限性是它是单峰分布。通过构造von Mises分布的混合分布，我们得到了一个灵活的框架，可以用来建模可处理多峰的周期变量

高斯混合分布Mixtures of Gaussians

• 如下图所示：这是Old Faithful数据集，包括272个在美国黄石国家公园Old Faithful间歇泉喷发的测量。每个测量包括喷发的持续时间(以分钟为单位)(横轴)和到下一次喷发的时间(以分钟为单位)(纵轴)。我们看到数据集形成两个主要的束，简单的高斯分布无法捕捉到这种结构，而两个高斯分布的线性叠加可以更好地描述数据集。左图是单高斯分布拟合情况，该分布难以捕获数据中的两个clumps，并且让大部分的概率质量分布在两个clumps之间的中间区域，而这里的数据相对稀疏；右图是两个高斯分布的线性组合的拟合情况，这能够给出更好的数据表示
  
• 这种叠加是由更基本的分布(如高斯分布)的线性组合形成的，可以表示为被称为混合分布的概率模型。下图是高斯的一个线性组合，给出非常复杂的密度。通过使用足够数量的高斯，并通过调整它们的均值和协方差以及线性组合中的系数，几乎任何连续密度都可以近似到任意精度
  
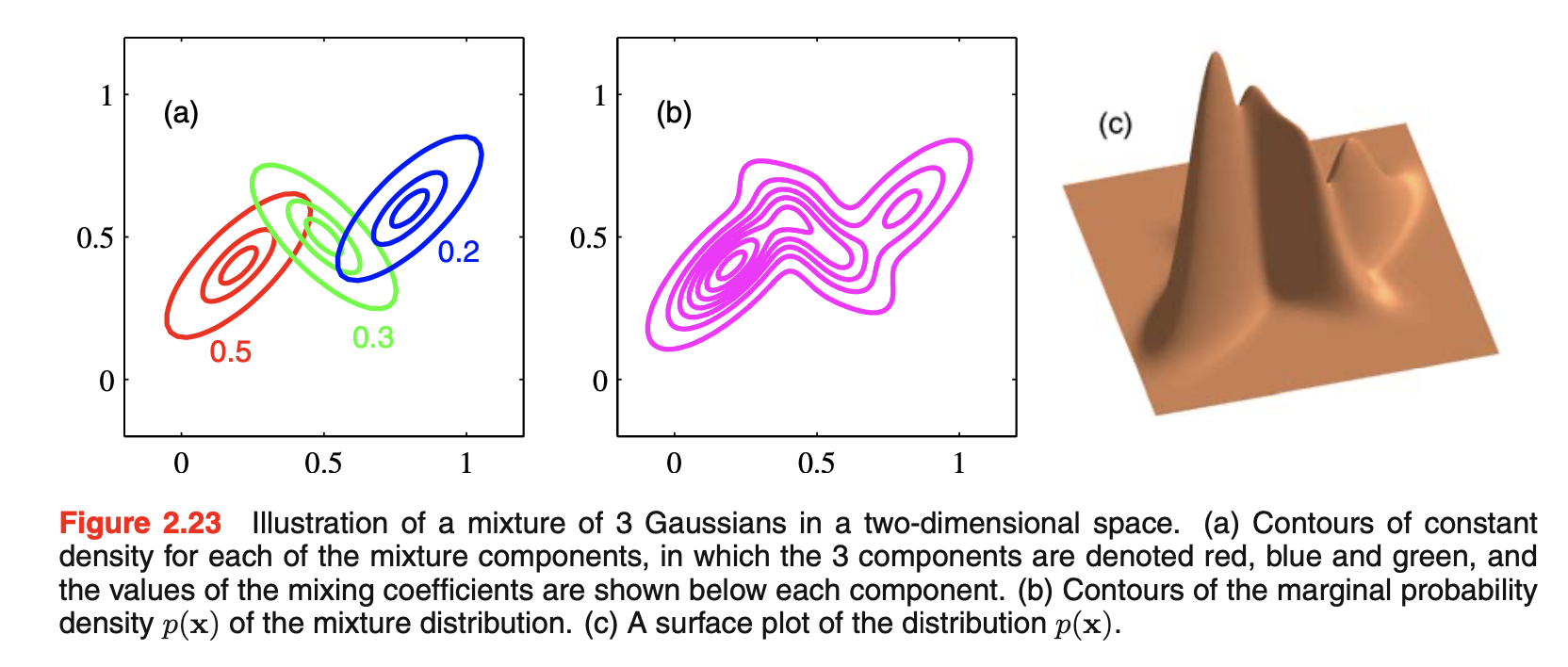
• 高斯混合: \(p(\vec{x})=\sum_{k=1}^K\pi_{k}N(\vec{x}|\vec{\mu}_k,\Sigma_k)\)，下图是具有三个成分的混合高斯的轮廓和surface。其中\(\pi_{k}\)满足概率的要求，即\(0\le \pi_{k}\le 1\)
  
• 混合模型可由其他分布的线性组合得到，如离散变量的混合模型可考虑贝努利分布混合
• 高斯混合分布的形式由参数\(\vec{\pi}\)、\(\vec{\mu}\)和\(\Sigma\)控制，其中\(\vec{\pi}=\{\pi_1,...,\pi_K\}\)，\(\vec{\mu}=\{\vec{\mu}_1,...,\vec{\mu}_K\}\)，\(\Sigma=\{\Sigma_1,...,\Sigma_K\}\)

指数族

• 除了高斯混合，这一章目前所学的分布都是指数族的具体例子，指数族成员都具有一些重要属性

代码实现

• 链接
• 二元变量
  • 继承随机变量基类(定义了fit、pdf和draw函数)(fit函数即进行分布参数的估计，可以是机器学习方法，也可以是贝叶斯方法)，定义Bernoulli分布，参数为\(\mu\)，参数也可由Beta给出(Beta给出\(\mu\)的先验)。Bernoulli分布参数\(\mu\)的机器学习估计为观测值的均值，贝叶斯估计为先验的01计数加上观测值的01计数

原书存疑的地方

• P75公式12.28中下标M是否应为K
• P89公式2.87中等号右边第二项中的-1指数是否应该有
• P91第一行的线性高斯的定义与P87最后一行的线性高斯的定义有出入