数学公式Latex语法快速入门

Latex语法

上下标--->^：上标 _：下标

• ^：上标
• _：下标

\sum_{i=1}^{n}X_n

\[\sum_{i=1}^{n}X_n \]

\int_{0}^{\infty}x^2dx

\(\int_{0}^{\infty}x^2dx\)

\prod_{i=1}^{n}X_n

\(\prod_{i=1}^{n}X_n\)

分数\(\frac{a}{b}\)<--->\frac{a}

使用\frac{}{}即可，例如\frac{a}{b}表示\(\frac{a}{b}\)

文字\(\text{hello,world!}\)<--->\text

\text{hello,world!}

\(\text{hello,world!}\)

矩阵、行列式

&表示分隔元素，\\表示换行

A=
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}

\[A= \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \]

A=
\begin{bmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{bmatrix}

\[A= \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \]

A=
\begin{Bmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{Bmatrix}

\[A= \begin{Bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{Bmatrix} \]

A=
\begin{vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{vmatrix}

\[A= \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} \]

A=
\begin{Vmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{Vmatrix}

\[A= \begin{Vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{Vmatrix} \]

A=
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{matrix}

\[A= \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \]

多行公式对齐--->\begin{split} \end

使用\begin{split} \end{split}，在需要对齐的地方添加&符号，注意需要用\\来换行

\begin{split}
L(\theta)
&=	\arg\max_{\theta}\ln(P_{All})\\
&=	\arg\max_{\theta}\ln\prod_{i=1}^{n}
    \left[
        (h_{\theta}(\mathbf{x}^{(i)}))^{\mathbf{y}^{(i)}}\cdot
        (1-h_{\theta}(\mathbf{x}^{(i)}))^{1-\mathbf{y}^{(i)}}
    \right]\\
&=	\arg\max_{\theta}\sum_{i=1}^{n}
	\left[
		\mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) +
		(1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
	\right]\\
&=	\arg\min_{\theta}
	\left[
        -\sum_{i=1}^{n}
        \left[
            \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) +
            (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
        \right]
	\right]\\
&=	\arg\min_{\theta}\mathscr{l}(\theta)
\end{split}

\[\begin{split} L(\theta) &= \arg\max_{\theta}\ln(P_{All})\\ &= \arg\max_{\theta}\ln\prod_{i=1}^{n} \left[ (h_{\theta}(\mathbf{x}^{(i)}))^{\mathbf{y}^{(i)}}\cdot (1-h_{\theta}(\mathbf{x}^{(i)}))^{1-\mathbf{y}^{(i)}} \right]\\ &= \arg\max_{\theta}\sum_{i=1}^{n} \left[ \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) + (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)})) \right]\\ &= \arg\min_{\theta} \left[ -\sum_{i=1}^{n} \left[ \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) + (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)})) \right] \right]\\ &= \arg\min_{\theta}\mathscr{l}(\theta) \end{split} \]

上例中，在=前添加了&，因此实现等号对齐；

\begin{split} \end{split}语法默认为右对齐，也就是说如果不在任何地方添加&符号，则公式默认右侧对齐，例如：

\begin{split}
L(\theta)
=	\arg\max_{\theta}\ln(P_{All})\\
=	\arg\max_{\theta}\ln\prod_{i=1}^{n}
    \left[
        (h_{\theta}(\mathbf{x}^{(i)}))^{\mathbf{y}^{(i)}}\cdot
        (1-h_{\theta}(\mathbf{x}^{(i)}))^{1-\mathbf{y}^{(i)}}
    \right]\\
=	\arg\max_{\theta}\sum_{i=1}^{n}
	\left[
		\mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) +
		(1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
	\right]\\
=	\arg\min_{\theta}
	\left[
        -\sum_{i=1}^{n}
        \left[
            \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) +
            (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
        \right]
	\right]\\
=	\arg\min_{\theta}\mathscr{l}(\theta)
\end{split}

\[\begin{split} L(\theta) = \arg\max_{\theta}\ln(P_{All})\\ = \arg\max_{\theta}\ln\prod_{i=1}^{n} \left[ (h_{\theta}(\mathbf{x}^{(i)}))^{\mathbf{y}^{(i)}}\cdot (1-h_{\theta}(\mathbf{x}^{(i)}))^{1-\mathbf{y}^{(i)}} \right]\\ = \arg\max_{\theta}\sum_{i=1}^{n} \left[ \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) + (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)})) \right]\\ = \arg\min_{\theta} \left[ -\sum_{i=1}^{n} \left[ \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) + (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)})) \right] \right]\\ = \arg\min_{\theta}\mathscr{l}(\theta) \end{split} \]

如果希望左对齐，例如(在需要左对齐的地方加&)

\begin{split}
&\ln h_{\theta}(\mathbf{x}^{(i)})
=	\ln\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}}
= 	-\ln(1+e^{\theta^T \mathbf{x}^{(i)}})\\
&\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
=	\ln(1-\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}})
= 	-\theta^T \mathbf{x}^{(i)}-\ln(1+e^{\theta^T \mathbf{x}^{(i)}})
\end{split}

\[\begin{split} &\ln h_{\theta}(\mathbf{x}^{(i)}) = \ln\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}} = -\ln(1+e^{\theta^T \mathbf{x}^{(i)}})\\ &\ln(1-h_{\theta}(\mathbf{x}^{(i)})) = \ln(1-\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}}) = -\theta^T \mathbf{x}^{(i)}-\ln(1+e^{\theta^T \mathbf{x}^{(i)}}) \end{split} \]

编号（这个在markdown实现不了）

只有一点不同：采用align环境会默认为每一条公式编号（如下例），split则不会编号。

\begin{align}
&\ln h_{\theta}(\mathbf{x}^{(i)})
=	\ln\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}}
	= -\ln(1+e^{\theta^T \mathbf{x}^{(i)}})\\
&\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
=	\ln(1-\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}})
	= -\theta^T \mathbf{x}^{(i)}-\ln(1+e^{\theta^T \mathbf{x}^{(i)}})
\end{align}

\[\begin{align} &\ln h_{\theta}(\mathbf{x}^{(i)}) = \ln\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}} = -\ln(1+e^{\theta^T \mathbf{x}^{(i)}})\\ &\ln(1-h_{\theta}(\mathbf{x}^{(i)})) = \ln(1-\frac{1}{1+e^{-\theta^T \mathbf{x}^{(i)}}}) = -\theta^T \mathbf{x}^{(i)}-\ln(1+e^{\theta^T \mathbf{x}^{(i)}}) \end{align} \]

方程组--->\begin{cases} \end

使用\begin{cases} \end{cases}

\begin{cases}
    \begin{split}
        p &= P(y=1|\mathbf{x})=
        	\frac{1}{1+e^{-\theta^T\mathbf{X}}}\\
        1-p &= P(y=0|\mathbf{x})=1-P(y=1|\mathbf{x})=
        	\frac{1}{1+e^{\theta^T\mathbf{X}}}
    \end{split}
\end{cases}

\[\begin{cases} \begin{split} p &= P(y=1|\mathbf{x})= \frac{1}{1+e^{-\theta^T\mathbf{X}}}\\ 1-p &= P(y=0|\mathbf{x})=1-P(y=1|\mathbf{x})= \frac{1}{1+e^{\theta^T\mathbf{X}}} \end{split} \end{cases} \]

公式和文字结合起来

\text{Decision Boundary}=
\begin{cases}
    1\quad \text{if }\ \hat{y}>0.5\\
    0\quad \text{otherwise}
\end{cases}

\[\text{Decision Boundary}= \begin{cases} 1\quad \text{if }\ \hat{y}>0.5\\ 0\quad \text{otherwise} \end{cases} \]

\quad表示空格

小写希腊字母

大写希腊字母

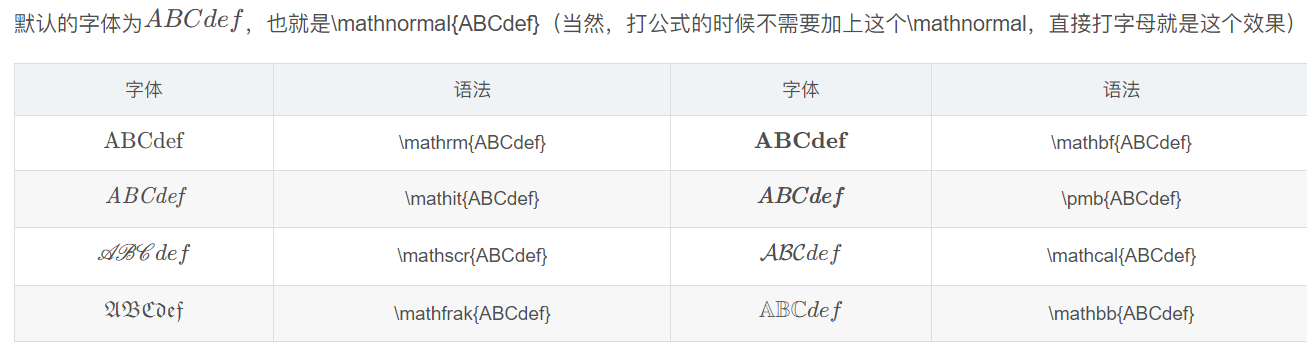
常用字体

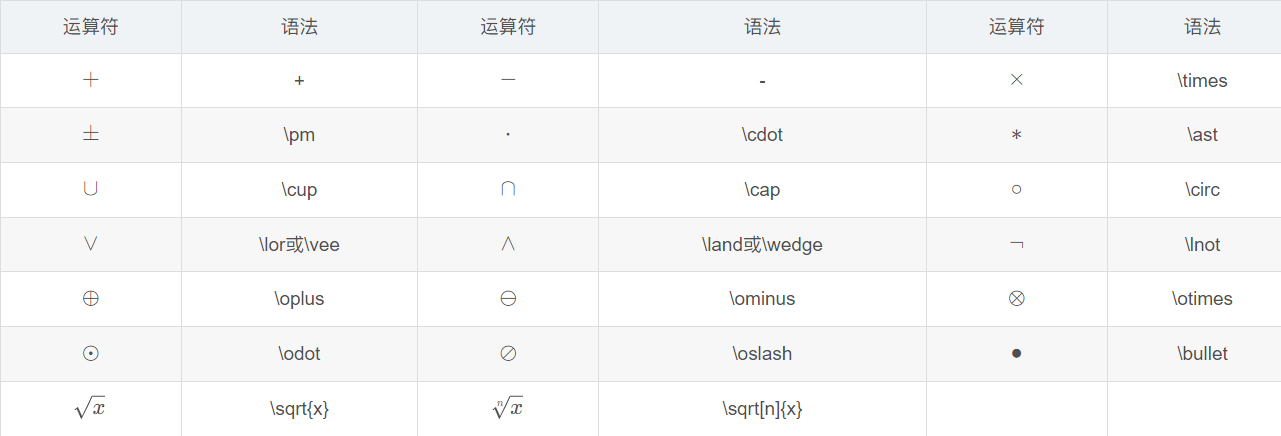
常见运算符

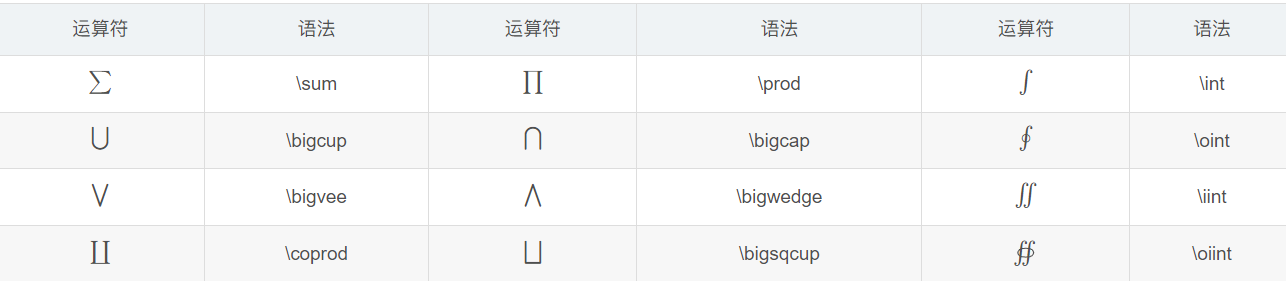
大尺寸运算符

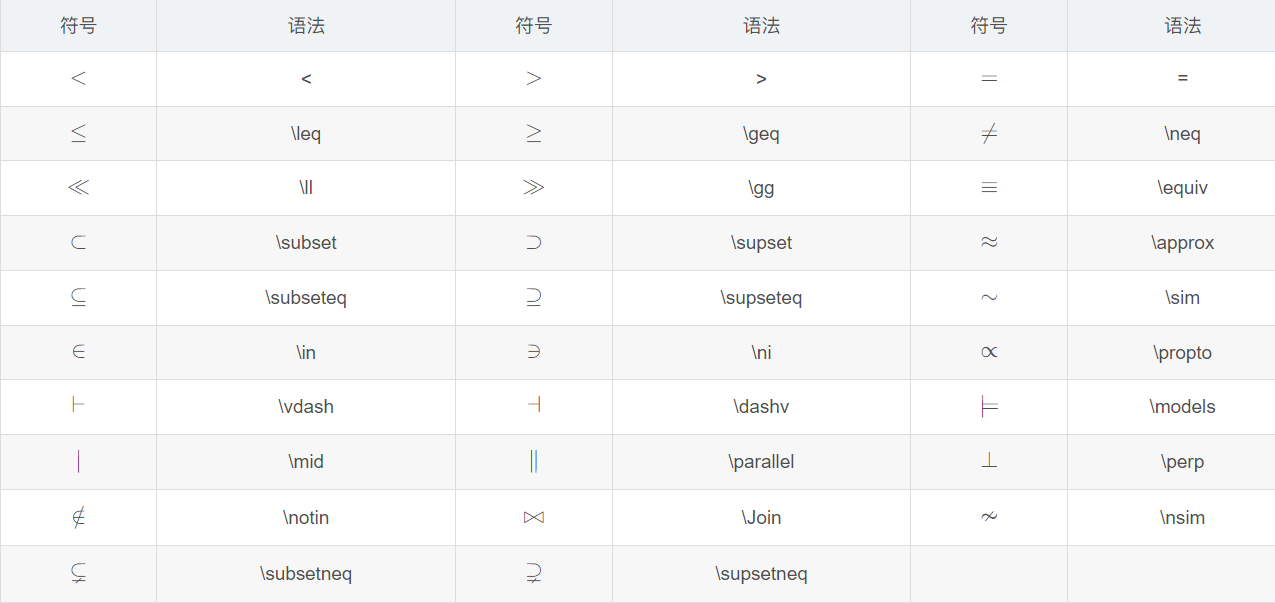
常见关系符号

数学模式重音符

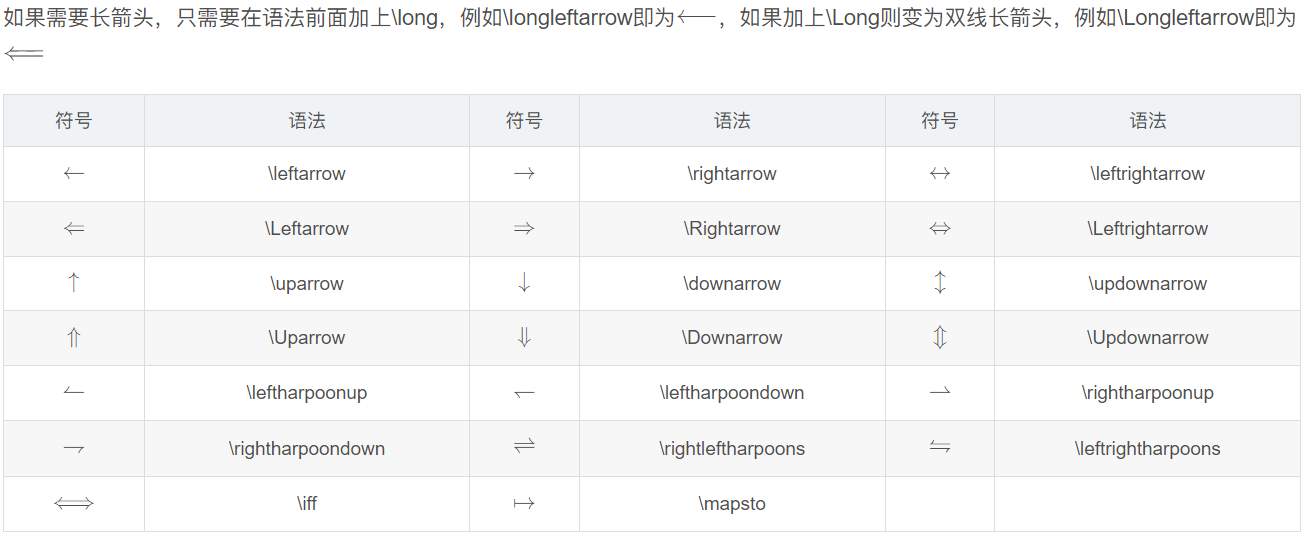
箭头

括号

大尺寸括号

注：大尺寸的()和[]是可以根据公式的高度自动调节的，例如

\arg\min_{\theta}
\left[
    -\sum_{i=1}^{n}
    \left[
        \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) +
        (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)}))
    \right]
\right]

\[\arg\min_{\theta} \left[ -\sum_{i=1}^{n} \left[ \mathbf{y}^{(i)}\ln(h_{\theta}(\mathbf{x}^{(i)})) + (1-\mathbf{y}^{(i)})\ln(1-h_{\theta}(\mathbf{x}^{(i)})) \right] \right] \]

可以看出，括号高度可以框住整个公式

因此在这种大型的公式中，使用大尺寸括号视觉效果更美观

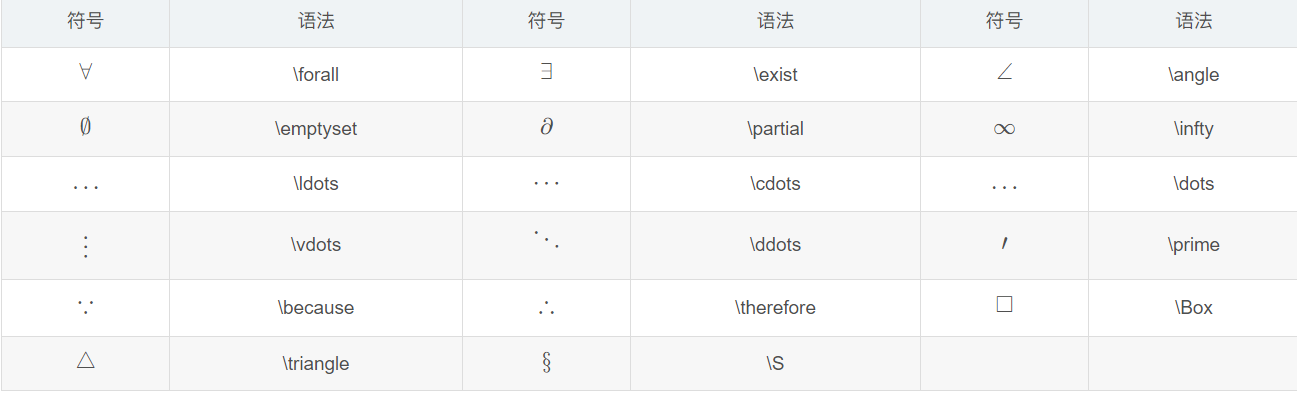
其他常见符号

常见函数

参考

参考：https://blog.csdn.net/Yushan_Ji/article/details/134322574