博客作业06--图
1.学习总结
1.1图的思维导图
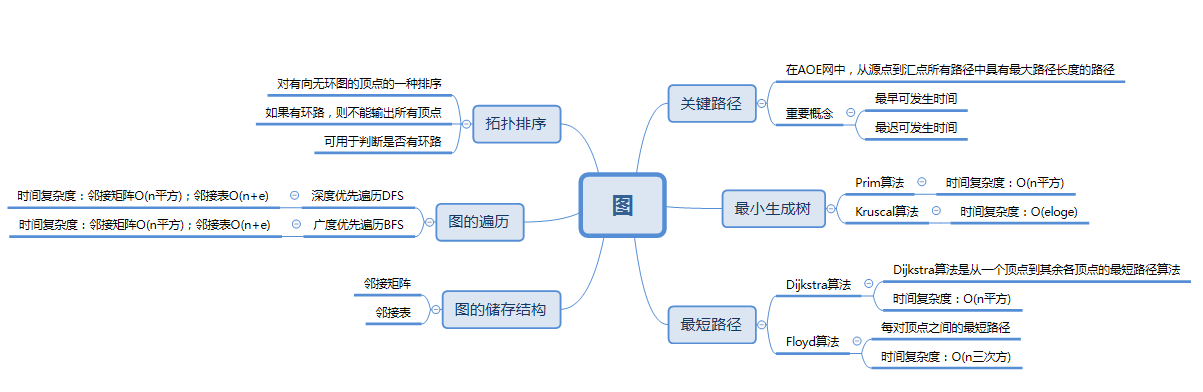
1.2 图结构学习体会
-
深度遍历算法和广度遍历算法:这两种算法是图的基本遍历算法,算法内容比较简单,运用广泛,很多算法都会运用到这个算法,是必须掌握的。
-
Prim和Kruscal算法:两种算法都是构造最小生成树的算法,不过两种算法的实现方法不同,Prim算法基于贪心算法进行优化,Kruscal算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法;两种算法各有优缺点,也是必须掌握的算法。
-
Dijkstra算法:Dijkstra算法是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题,算法比较复杂,需要加强理解。
-
拓扑排序算法:拓扑排序是对有向无环图的顶点的一种排序,它使得如果存在Vi到Vj的路径,那么在排序中Vj出现在Vi的后面;如果有环路,则不能输出所有顶点。
2.PTA实验作业
2.1 题目1:排座位
2.2 设计思路
定义Relation数组保存宾客之间的关系,indirect数组保存间接关系
for i=1 to m{
输入宾客之间的关系,保存到Relation数组中
如果是朋友关系,保存到indirect数组中}
三重循环,发现有间接朋友关系,保存到indirect数组中
for i=1 to k{
if Relation[a][b]==1
为朋友关系
else if Relation[a][b]==0&&indirect[a][b]==1
为间接朋友关系
else if Relation[a][b]==0
没有敌对关系
else if indirect[a][b]==1
之间有敌对,然而也有共同的朋友
else 敌对关系
2.3 代码截图

2.4 PTA提交列表说明

2.1 题目2:六度空间
2.2 设计思路
BFS函数:
定义变量level保存当前遍历层数,last保存每层最后一个结点
初始v入队列
while(队不空){
出队列
广度遍历,count累计有多少个结点
当遍历到每层最后一个结点时
level加一
更新last值
当level>=6时,结束循环
}
weight=((1.0*count)/n)*100;
BFS1函数
重复调用BFS函数n次,计算每个结点
2.3 代码截图

2.4 PTA提交列表说明
本题刚开始时,我并不会做,虽然老师上课有讲过一点,但是实际上还是不知道该怎么写,后来还是上网查了一下,发现用level来记录当前是哪一层的方法来实现,很巧妙。
2.1 题目3:旅游规划
2.2 设计思路
置edges[head][head]为0
初始化vis,path,a数组
置a[head],cost[head]为0
for(i=0;i<n;i++){
定义mina=INF,k=INF
循环选取不在vis中具有最短距离的顶点k
k加入vis数组
for(j=0;j<n;j++){
当距离有更小的时候,更新a数组和cost数组的值
当距离一样时,选择花费较小的,更新cost数组}
}
2.3 代码截图

2.4 PTA提交列表说明
刚开始时一直部分正确,一直想不通是哪里错了,后来重新理清思路,浏览一下代码,发现原来是邻接矩阵初始化问题,因为这是个带权图,所以不能初始化为0。
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分:
255
4. 阅读代码
问题描述:n个村庄之间的无向图,边上的权值w(i,j)表示村庄i和j之间道路长度.现要从这n个村庄中选择一个村庄新建一所医院,使离医院最远的村庄到医院的路程最短.设计一程序求解此问题
#include <iostream>
using namespace std;
#define INF 32767
#define MaxVex 20
typedef enum {DG,DN,UDG,UDN}GraphKind;
bool path[MaxVex][MaxVex]={};
bool final[MaxVex];
int D[MaxVex]={0};
int d[MaxVex]={0};
struct ArcCell{
int adj;
int *info;
};
struct Graph{
int vexs[MaxVex];
ArcCell arcs[MaxVex][MaxVex];
int vexnum,arcnum;
GraphKind kind;
};
int getmax(int *d,Graph a)
{
int result=0;
for(int i=0;i<a.vexnum;i++)
if(result<d[i])result=d[i];
return result;
}
int getmin(int *d,Graph a)
{
int result=d[0];
int i,j;
for(i=0;i<a.vexnum;i++)
if(result>d[i]){result=d[i];j=i;}
return j;
}
void input(Graph *graph)
{
int n;
cout<<"请输入顶点个数";
cin>>n;
graph->vexnum=n;
cout<<endl<<"请输入无向图的邻接矩阵,无穷时大请输入-1";
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
cout<<endl<<"arc["<<i<<"]["<<j<<"]=";
cin>>graph->arcs[i][j].adj;
if(graph->arcs[i][j].adj==-1)graph->arcs[i][j].adj=INF;
/*if(i==j){graph->arcs[i][j].adj=0;cout<<endl<<"arc["<<i<<"]["<<j<<"]=0";}
else if(graph->arcs[j][i].adj>0&&graph->arcs[j][i].adj<=INF){graph->arcs[i][j].adj=graph->arcs[j][i].adj;cout<<endl<<"arc["<<i<<"]["<<j<<"]="<<graph->arcs[j][i].adj;}
else {cout<<endl<<"arc["<<i<<"]["<<j<<"]=";cin>>graph->arcs[i][j].adj;}
if(graph->arcs[i][j].adj==-1)graph->arcs[i][j].adj=INF;
*/
}
}
void Dijkstra(Graph G,int v0)
{
int min,v,w;
for(v=0;v<G.vexnum;++v){
final[v]=false; D[v]=G.arcs[v0][v].adj;
for(int w=0;w<G.vexnum;++w) path[v][w]=false;
if(D[v]<INF){path[v][v0]=true;path[v][v]=true;}
}//for
D[v0]=0; final[v0]=true;
for(int i=1;i<G.vexnum;++i){
min=INF;
for(w=0;w<G.vexnum;++w)
if(!final[w])
if(D[w]<min){v=w;min=D[w];}
final[v]=true;
for(w=0;w<G.vexnum;++w)
if(
!final[w]&&(min+G.arcs[v][w].adj<D[w])){
D[w]=min+G.arcs[v][w].adj;
for(int j=0;j<MaxVex;j++)path[w][j]=path[v][j];
path[w][w]=true;
}//if
}//for
}//dij
void shortpath(Graph a)
{
int result;
for(int i=0;i<a.vexnum;i++)
{
Dijkstra(a,i);
d[i]=getmax(D,a);//D[i]为始点到第i个点的最短路径
//d[i]为始点为i时到其他各点最短路径中的最长路径;
}
result=getmin(d,a);
Dijkstra(a,result);//getmin(d)为结果,医院位置
for(int j=0;j<a.vexnum;j++)
{
cout<<endl<<"从医院(点"<<result+1<<")到村庄(点"<<j+1<<")最短距离为"<<D[j]<<"线路为";
int x=0;
for(int i=0;i<a.vexnum;i++)
{
if(path[j][i]==true)
{
x++;
if(x>1)cout<<"->";
cout<<i+1;
}
}
}
}
void main()
{
Graph a;
input(&a);
shortpath(a);
}
这是一道有关求最短路径的问题,但是它又有所不同,它要求使离医院最远的村庄到医院的路程最短,这就需要在原来的算法中进行改进,找出村庄i和全部村庄的最短路径,记录这些最短路径中的最大值Si,得到全部村庄的最大值集合{S1,S2,。。。},集合中的最小值,就是所求村庄。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号