CSP-S突破营day5

### 树形dp

基于树的dp

- dp 方法始终为从下至上进行 dp。
- 在每个节点对所有儿子做聚合。
- 可能需要多一遍 dfs 或者 bfs。

如何存图？

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
vector<int> z[maxn];//z[i][j]代表从i出发的第j条边会走到z[i][j]
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n;
for(int i = 1;i < n;i++){
int p1, p2;
cin >> p1 << p2;
z[p1].push_back(p2);
z[p2].push_back(p1);
}
return 0;
}
```

-----

##### 例一

有 $n$ 个点的树有多少个点？

首先，树形 dp 中 **$f[i]$ 一定代表以 $i$ 为根的子树有多少个点**。

$z[i][j]$ 代表从 $i$ 出发的第 $z[i][j]$，计算 $f[i]$ $i$的父亲是谁。

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
vector<int> z[maxn];//z[i][j]代表从i出发的第j条边会走到z[i][j]
int f[maxn];//f[i]以 i 为根的子树有多少个点
void dfs(int i, int fa){//计算f[i] i的父亲是谁
//求i的所有儿子的f值
for(auto j : z[i]){//枚举z[i]中的所有东西 这是一条从i到j的边
if(j != fa){
dfs(j, i);
}
}
//把自己的f值算出来
f[i] = 1;
for(auto j : z[i]){//枚举z[i]中的所有东西 这是一条从i到j的边
if(j != fa){
f[i] += f[j];
}
}
//最好把两个循环拆开！！！
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n;
for(int i = 1;i < n;i++){
int p1, p2;
cin >> p1 >> p2;
z[p1].push_back(p2);
z[p2].push_back(p1);
}
dfs(1, 0);
cout << n << '\n';
return 0;
}
```

注意：

在 dfs 中最好把两个循环拆开！！！

----

##### 例二

$$\displaystyle \sum^n_{i=1}\sum^n_{j=i+1}\text{dis}(i, j)$$

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
vector<int> z[maxn];//z[i][j]代表从i出发的第j条边会走到z[i][j]
int f[maxn];//f[i]以 i 为根的子树有多少个点
void dfs(int i, int fa){//计算f[i] i的父亲是谁
//求i的所有儿子的f值
for(auto j : z[i]){//枚举z[i]中的所有东西 这是一条从i到j的边
if(j != fa){
dfs(j, i);
}
}
//把自己的f值算出来
f[i] = 1;
for(auto j : z[i]){//枚举z[i]中的所有东西 这是一条从i到j的边
if(j != fa){
f[i] += f[j];
}
}
//最好把两个循环拆开！！！
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n;
for(int i = 1;i < n;i++){
int p1, p2;
cin >> p1 >> p2;
z[p1].push_back(p2);
z[p2].push_back(p1);
}
dfs(1, 0);
int ans = 0;
for(int i = 1;i <= n;i++){
ans += f[i] * (n - f[i]);
}
cout << ans << '\n';
return 0;
}
```

----

##### 例三

求树的直径。

![](https://cdn.luogu.com.cn/upload/image_hosting/vtzh8d7h.png)

即求 $\max \text{dis}(i,j)$。

$f[i]$ 代表从 $i$ 向下最长能走多长，$g[i]$ 从 $i$ 次长。

```CPP
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
vector<int> z[maxn];//z[i][j]代表从i出发的第j条边会走到z[i][j]
int f[maxn];//f[i]以i向下最长能走多长
int g[maxn];//次长
void dfs(int i, int fa){//计算f[i] i的父亲是谁
//求i的所有儿子的f值
for(auto j : z[i]){//枚举z[i]中的所有东西 这是一条从i到j的边
if(j != fa){
dfs(j, i);
}
}
//把自己的f值算出来
f[i] = 1;
for(auto j : z[i]){//枚举z[i]中的所有东西 这是一条从i到j的边
if(j != fa){
int l =f[j] + 1;
if(l > f[i]){
g[i] = f[i];
f[i] = l;
}
else{
g[i] = max(g[i], l);
}
}
}
//最好把两个循环拆开！！！
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n;
for(int i = 1;i < n;i++){
int p1, p2;
cin >> p1 >> p2;
z[p1].push_back(p2);
z[p2].push_back(p1);
}
dfs(1, 0);
int ans = 0;
for(int i = 1;i <= n;i++){
ans = max(ans, f[i] + g[i]);
}
cout << ans << '\n';
return 0;
}
```

----

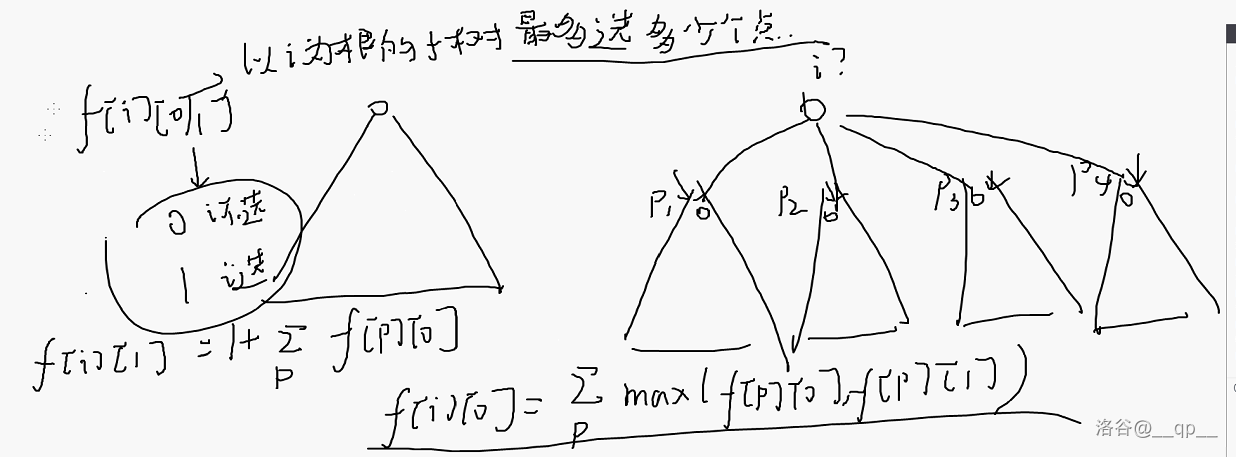
##### Problem 4

询问树的最大独立集。

注意到：

$$dp[u][0] = \sum_{i = 1}^{k} \max(dp[v_i][0], dp[v_i][1])$$

$$dp[u][1] = 1 + \sum_{i = 1}^{k} dp[v_i][0]$$

![](https://cdn.luogu.com.cn/upload/image_hosting/t1qbryr2.png)

```cpp
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 10005;
vector<int> a[MAXN];
int dp[MAXN][2];
void dfs(int u, int fa){
dp[u][0] = 0;
dp[u][1] = 1;
for(int v : a[u]){
if(v != fa){
dfs(v, u);
dp[u][0] += max(dp[v][0], dp[v][1]);
dp[u][1] += dp[v][0];
}
}
}

int main(){
int n;
cin >> n;
for(int i = 0;i < n - 1;i++){
int u, v;
cin >> u >> v;
a[u].push_back(v);
a[v].push_back(u);
}
dfs(1, -1);
int ans = max(dp[1][0], dp[1][1]);
cout << ans << '\n';
return 0;
}
```

-----

### 排列dp

##### 例一

$1\sim n$ 的排列有多少个排列有偶数个逆序对？

$f[i]$ 代表从小到大 $1\sim i$ 放好了/从大到小 $n\sim i$ 放好了。

时间复杂度为 $O(n^4)$。

代码：

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
int f[maxn][2];//f[i][j]已经把1~i放好 有j个逆序对的方案数
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n;
f[0][0] = 1;
for(int i = 1;i <= n;i++){//要放i这个数
for(int j = 0;j <= (i - 1) * (i - 2) / 2;j++){//以f[i-1][j]向外转移
for(int k = 0;k <= i - 1;k++){//枚举i要放在第几个位置
f[i][j + i - 1 - k] += f[i - 1][j];
}
}
}
return 0;
}
```

时间复杂度为 $O(n^3)$。

代码：

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n;
int f[maxn][2];//f[i][j]已经把1~i放好 有j个逆序对的方案数
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n;
f[0][0] = 1;
for(int i = 1;i <= n;i++){//要放i这个数
for(int j = 0;j <= 1;j++){//以f[i-1][j]向外转移
for(int k = 0;k <= i - 1;k++){//枚举i要放在第几个位置
f[i][(j + i - 1 - k) % 2] += f[i - 1][j];
}
}
}
return 0;
}
```

----

##### 例二

$1\sim n$ 的排列，$a_i$ 比 $1\sim a_{i-1}$ 都大，称 $a_i$ 时激动的，激动值为 $a_i$。求激动值为 $k$ 的个数。

$f[i][j]$ 代表从大到小激动值为 $j$ 的方案数。

$$dp[i][j] = dp[i-1][j-1] + dp[i-1][j]\times(i-1)$$

```cpp
#include <iostream>
using namespace std;
int dp[1005][1005];
int n, k;
int main(){
cin >> n >> k;
dp[0][0] = 1;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= i;j++){
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] * (i - 1);
}
}
cout << dp[n][k] << '\n';
return 0;
}
```

----

### 区间dp

#### 第一类

##### 例一

合并石子，每次选择相邻两堆，代价为两堆石子和，求最小总代价。

$f[l][r]$ 表示第 $l\sim r$ 堆石子合并为一堆的最大代价。

初始化 $f[i][i]=0$。

$$\displaystyle f[l][r]=\min_{l\le k<r}(f[l][k]+f[k+1][r]+sum[r]-sum[l-1])$$

![](https://cdn.luogu.com.cn/upload/image_hosting/5dhkcneq.png)

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n, a[maxn], sum[maxn];
int f[maxn][maxn];//f[l][r]表示把第l~r堆石子合并为一堆的最小代价
int main(){
cin.tie(0) -> sync_with_stdio(0);
//O(n^3) n<=200
cin >> n;
for(int i = 1;i <= n;i++){
cin >> a[i];
sum[i] = sum[i - 1] + a[i];
}
memset(f, 0x3f, sizeof(f));
for(int i = 1;i <= n;i++){
f[i][i] = 0;
}
for(int len = 2;len <= n;len++){//区间长度
for(int l = 1, r = len;r <= n;l++, r++){
for(int k = l;k < r;k++){
f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + sum[r] - sum[l - 1]);
}
}
}
cout << f[1][n];
return 0;
}
```

----

例二

一个环，合并石子，每次选择相邻两堆，代价为两堆石子和，求最小总代价。

```cpp
#include<bits/stdc++.h>
using namespace std;
int n,a[2333],sum[2333],f[2333][2333];
int main(){
cin>>n;
for(int i=1;i<=n;i++) {
cin>>a[i];
sum[i]=sum[i-1]+a[i];
}
for(int i=n+1;i<=n+n;i++){
a[i]=a[i-n];
sum[i]=sum[i-1]+a[i];
}
memset(f,0x3f,sizeof(f));
for(int i=1;i<=n+n;i++){
f[i][i]=0;
}
for(int len=2;len<=n;len++){
for(int l=1,r=len;r<=n+n;r++,l++){
for(int k=l;k<r;k++){
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+sum[r]-sum[l-1]);
}
}}
int ans=f[1][n];
for(int i=2;i<=n;i++){
ans=min(ans,f[i][i+n-1]);
}
for(int len=2;len<=n;len++){
for(int l=1,r=len;r<=n+n;r++,l++){
for(int k=l;k<r;k++){
f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+sum[r]-sum[l-1]);
}
}
}
int ans2=f[1][n];
for(int i=2;i<=n;i++){
ans2=max(ans2,f[i][i+n-1]);
}
cout<<ans<<endl;
cout<<ans2<<endl;
return 0;
}
```

----

#### 第二类

给定字符串，求回文子序列的数量

$$dp[i][j]=dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1] (if(str[i]\not=str[j]))$$

$$dp[i][j]=dp[i+1][j] + dp[i][j-1] - dp[i+1][j-1]+dp[i+1][j-1]+1=dp[i+1][j] + dp[i][j-1]+1 (if(str[i]==str[j]))$$

```cpp
#include <iostream>
#include <vector>
using namespace std;

int f(string str) {
int len = str.length();
vector<vector<int> > dp(len, vector<int>(len));

for (int j = 0; j < len; j++) {
dp[j][j] = 1;
for (int i = j - 1; i >= 0; i--) {
dp[i][j] = dp[i + 1][j] + dp[i][j - 1] - dp[i + 1][j - 1];
if (str[i] == str[j])
dp[i][j] += 1 + dp[i + 1][j - 1];
}
}
return dp[0][len - 1];
}

int main() {
string str;
int num;
while (cin >> str) {
num = f(str);
cout << num << endl;
}
return 0;
}
```

## 图论

### 图的定义：

- 图 $G$ 是一个有序二元组 $(V,E)$，其中 $V$ 称为点集（Vertices Set），$E$ 称为边集（Edges set）。
- 有向图、无向图：如果给图的每条边规定一个方向，那么得到的图称为有向图。在有向图中，与一个节点相关联的边有出边和入边之分。相反，边没有方向的图称为无向图。

- 度（Degree）：一个顶点的度是指与该顶点相关联的边的条数，顶点 $v$ 的度记作 $d(v)$。
- 入度（In-degree）和出度（Out-degree）：对于有向图来说，一个顶点的度可细分为入度和出度。一个顶点的入度是指与其关联的各边之中，以其为终点的边数；出度则是相对的概念，指以该顶点为起点的边数。
- 自环（Loop）：若一条边的两个顶点为同一顶点，则此边称作自环。
- 路径（Path）

### 特殊的图

#### 树

无环、无向图

$n$ 个点的树有 $n-1$ 条边。

#### 森林

无环、无向图（很多树组成的不一定连通的图）

#### 树的扩展

章鱼图、基环图（将森林用一个换连接起来）。

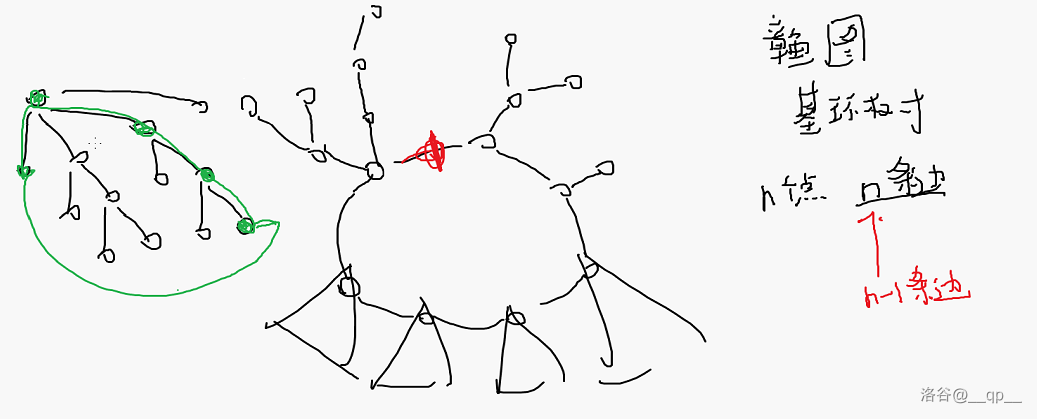
![](https://cdn.luogu.com.cn/upload/image_hosting/t88a5o10.png)

在一棵树的任意两个点上加上一条边可以形成一个环，故可形成一个章鱼图。

#### 仙人掌图

边仙人掌、点仙人掌

##### 边仙人掌：

每一条边只能在一个环里

##### 点仙人掌：

每一条点只能在一个环里

#### 二分图、偶图

将这个图分为两边，剩下的边只能在中间（树就是一个二分图，因为相邻的两层一定是一奇一偶，奇不可能相连奇，偶同样）。

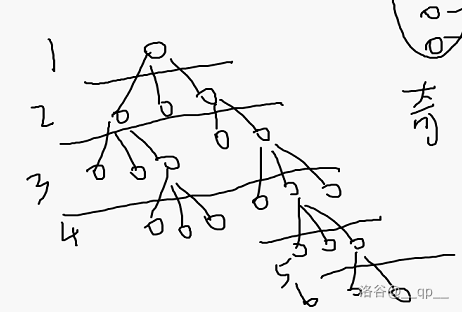
![](https://cdn.luogu.com.cn/upload/image_hosting/hsqx4bfp.png)

![](https://cdn.luogu.com.cn/upload/image_hosting/pq8oswgj.png)

有奇环 $\iff$ 不是二分图

无奇环 $\iff$ 一定是二分图

----

### 图的遍历

BFS、DFS、图染色。## 图论

### 图的定义：

- 图 $G$ 是一个有序二元组 $(V,E)$，其中 $V$ 称为点集（Vertices Set），$E$ 称为边集（Edges set）。
- 有向图、无向图：如果给图的每条边规定一个方向，那么得到的图称为有向图。在有向图中，与一个节点相关联的边有出边和入边之分。相反，边没有方向的图称为无向图。

- 度（Degree）：一个顶点的度是指与该顶点相关联的边的条数，顶点 $v$ 的度记作 $d(v)$。
- 入度（In-degree）和出度（Out-degree）：对于有向图来说，一个顶点的度可细分为入度和出度。一个顶点的入度是指与其关联的各边之中，以其为终点的边数；出度则是相对的概念，指以该顶点为起点的边数。
- 自环（Loop）：若一条边的两个顶点为同一顶点，则此边称作自环。
- 路径（Path）

### 特殊的图

#### 树

无环、无向图

$n$ 个点的树有 $n-1$ 条边。

#### 森林

无环、无向图（很多树组成的不一定连通的图）

#### 树的扩展

章鱼图、基环图（将森林用一个换连接起来）。

![](https://cdn.luogu.com.cn/upload/image_hosting/t88a5o10.png)

在一棵树的任意两个点上加上一条边可以形成一个环，故可形成一个章鱼图。

#### 仙人掌图

边仙人掌、点仙人掌

##### 边仙人掌：

每一条边只能在一个环里

##### 点仙人掌：

每一条点只能在一个环里

#### 二分图、偶图

将这个图分为两边，剩下的边只能在中间（树就是一个二分图，因为相邻的两层一定是一奇一偶，奇不可能相连奇，偶同样）。

![](https://cdn.luogu.com.cn/upload/image_hosting/hsqx4bfp.png)

![](https://cdn.luogu.com.cn/upload/image_hosting/pq8oswgj.png)

有奇环 $\iff$ 不是二分图

无奇环 $\iff$ 一定是二分图

----

### 图的遍历

BFS、DFS、图染色。

##### Problem 1

给定一张无向图，判断是否为二分图。

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n, m;
vector<int> z[maxn];//z[i][j]代表从i出发的第j条边会走到z[i][j]
int col[maxn];//col[i]i点的颜色col[i]=0未染色=1左=2右
void dfs(int s){//当前要对i周围的点染色
for(auto j : z[i]){
if(col[j] == 0){//j点未染色
col[j] = 3 - col[i];
dfs(j);
} else {
if(col[j] == col[i]){
cout << "No\n";
exit(0);
}
}
}
}
//O(n + m)
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n >> m;
for(int i = 1;i <= m;i++){
int p1, p2;
cin >> p1 >> p2;
z[p1].push_back(p2);
z[p2].push_back(p1);
}
for(int i = 1;i <= n;i++){
if(col[i] == 0){
dfs(i);//不要求连通
}
}
cout << "Yes\n";
return 0;
}
```

-----

#### 二分图匹配

匹配如图：

![](https://cdn.luogu.com.cn/upload/image_hosting/4o43i1ug.png)

给你二分图，最多匹配多少对？

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n, m, k;//n代表左边有几个点，m代表右边有几个点 k代表有几条边
vector<int> z[maxn];
bool use[maxn];//use[i]代表代表在这一轮中 右边第r个点有没有被请求过
int match[maxn];//match[i]代表当前右边第r个点是和左边第match[r]匹配
bool dfs(int l){//让左边第l个点去尝试匹配返回是否成功
//O(n+k)
for(auto r : z[l]){//让左边第l个点和右边第r个点尝试匹配
if(use[r] = false){//这一轮中右边r第个人还没有被请求匹过
use[r] = true;
if(match[r] == 0 || dfs(match[r])){
match[r] = l;//匹配成功
return true;
}
}
}
return false;//匹配失败
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n >> m >> k;
for(int i = 1;i <= k;i++){//只用从左向右连边
int l, r;
cin >> l >> r;
z[l].push_back(r);
}
int ans = 0;
for(int i = 1;i <= n;i++){
memset(use, false, sizeof(use));
if(dfs(i)){
ans++;
}
}
cout << ans;
return 0;
}
```

#### 匈牙利算法

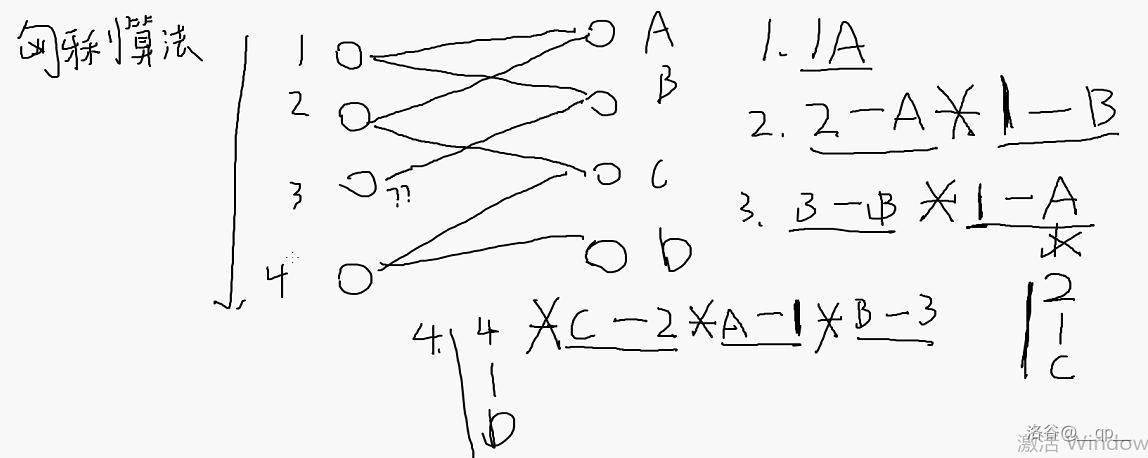
![](https://cdn.luogu.com.cn/upload/image_hosting/m1zyfogl.png)

用 dfs（让左边第 $l$ 个点去尝试匹配返回是否成功），$n$ 代表左边有几个点，$m$ 代表右边有几个点 $k$ 代表有几条边。

我们只用从左向右连边即可。

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 10;
int n, m, k;//n代表左边有几个点，m代表右边有几个点 k代表有几条边
vector<int> z[maxn];
bool use[maxn];//use[i]代表代表在这一轮中 右边第r个点有没有被请求过
int match[maxn];//match[i]代表当前右边第r个点是和左边第match[r]匹配
bool dfs(int l){//让左边第l个点去尝试匹配返回是否成功
//O(n+k)
for(auto r : z[l]){//让左边第l个点和右边第r个点尝试匹配
if(use[r] = false){//这一轮中右边r第个人还没有被请求匹过
use[r] = true;
if(match[r] == 0 || dfs(match[r])){
match[r] = l;//匹配成功
return true;
}
}
}
return false;//匹配失败
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n >> m >> k;
for(int i = 1;i <= k;i++){//只用从左向右连边
int l, r;
cin >> l >> r;
z[l].push_back(r);
}
int ans = 0;
for(int i = 1;i <= n;i++){
memset(use, false, sizeof(use));
if(dfs(i)){
ans++;
}
}
cout << ans;
return 0;
}
```

-----

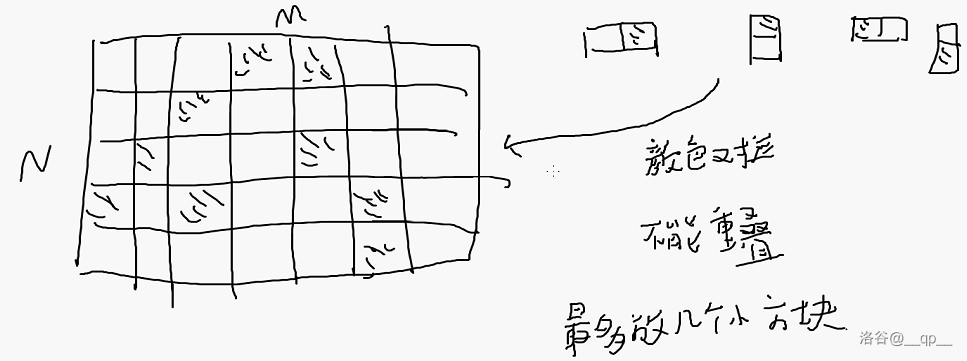
![](https://cdn.luogu.com.cn/upload/image_hosting/uhhocwcp.png)

原题转化为最多有几个匹配，即最多几个小方块。

 

----

![](https://cdn.luogu.com.cn/upload/image_hosting/vpvwb9ib.png)

即最多几个匹配

----

## 最短路

最短路包括多源最短路（多个点之间），单源最短路。

$dist[i][j]$ 表示从 $i$ 到 $j$ 的最短路。

$$dist[i][j]\le dist[i][k]+dist[k][j]$$

当且仅当 $i,j,k$ 共线时最短（三角不等式）。

### 多源最短路

floyd 本质是动态规划。

$dist[i][j][k]$ 表示从 $j$ 走到 $k$ 其中中间的节点的编号都 $\le i$ 的最短路径长度，最后输出 $dist[n][i][k]$。

首先初始化 $dist[0][i][i]=0$。

$$dist[i][j][k]=\min(dist[i-1][j][k],dist[i - 1][j][i] + dist[i - 1][i][k])$$

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e2 + 10;
int n, m;
int dist[maxn][maxn];//dist[i][j][k]从i走到k使得中间经过的节点编号<=i最短路长度

int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n >> m;
memset(dist, 0x3f, sizeof(dist));
for(int i = 1;i <= n;i++){
dist[i][i] = 0;
}
for(int i = 1;i <= m;i++){
int p1, p2, d;
cin >> p1 >> p2 >> d;
dist[p1][p2] = min(dist[p1][p2], d);
dist[p2][p1] = min(dist[p2][p1], d);
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
for(int k = 1;k <= n;k++){
dist[j][k] = min(dist[j][k], dist[j][i] + dist[i][k]);
}
}
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
cout << dist[i][j] << " ";
}
cout << '\n';
}
return 0;
}

```

----

### 单源最短路

#### dijkstra

必须保证边权非负！

每次取 $dist$ 值最小的边。

时间复杂度为 $O(n^2+m)$。

```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n, m;
vector<pair<int, int> > z[maxn];
int dist[maxn];//dist[i]代表从起点到i的最短路长度
bool use[maxn];//use[i]代表i点有没有被选过
void dij(int s){
memset(dist, 0x3f, sizeof(dist));
//O(n^2+m)
dist[s] = 0;
for(int i = 1;i <= n;i++){//执行n轮
int p = 0;
for(int j = 1;j <= n;j++){
if(!use[j] && dist[j] <= dist[p]){
p = j;
}
}
use[p] = true;
for(auto x : z[p]){//O(m)
int q = x.first;
int d = x.second;//是一条从p->q长度为d的边
if(dist[q] > dist[p] + d){
dist[q] = dist[p] + d;
}
}
}
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n >> m;
for(int i = 1;i <= m;i++){
int p1, p2, d;//从p1到p2长度为d的边
cin >> p1 >> p2 >> d;
z[p1].push_back(make_pair(p2, d));
}
dij(1);
return 0;
}

```

注意到可以用堆优化。

时间复杂度：

STL堆：$O((n+m)\log(n+m))$。

手写堆：$O((n+m)\log n)$。

```### 树形dp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n, m;
vector<pair<int, int> > z[maxn];
int dist[maxn];//dist[i]代表从起点到i的最短路长度
bool use[maxn];//use[i]代表i点有没有被选过
void dij(int s){
memset(dist, 0x3f, sizeof(dist));
//O(n^2+m)
dist[s] = 0;
priority_queue<pair<int, int> > heap;//first最短路的长度 second点的编号
for(int i = 1;i <= n;i++){
heap.push(make_pair(-dist[i], i));
}
for(int i = 1;i <= n;i++){//执行n轮
//STL堆：O((n+m)log(n+m))
//手写堆：O((n+m)logn)
while(use[heap.top().second]){
heap.pop();//堆优化
}
int p = heap.top().second;
heap.pop();

use[p] = true;
for(auto x : z[p]){//O(m)
int q = x.first;
int d = x.second;//是一条从p->q长度为d的边
if(dist[q] > dist[p] + d){
dist[q] = dist[p] + d;
heap.push(make_pair(-dist[q], q));
}
}
}
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> n >> m;
for(int i = 1;i <= m;i++){
int p1, p2, d;//从p1到p2长度为d的边
cin >> p1 >> p2 >> d;
z[p1].push_back(make_pair(p2, d));
}
dij(1);
return 0;
}
```

posted @ 2025-01-26 21:01  Yantai_YZY  阅读(13)  评论(0)    收藏  举报