CSP-S突破营day3

##### 例一

第一行包含两个正整数 $N,M$，分别表示数列中实数的个数和操作的个数。

第二行包含 $N$ 个实数，其中第 $i$ 个实数表示数列的第 $i$ 项。

接下来 $M$ 行，每行为一条操作，格式为以下三种之一：

操作 $1$：`1 x y k` ，表示将第 $x$ 到第 $y$ 项每项加上 $k$，$k$ 为一实数。
操作 $2$：`2 x y` ，表示求出第 $x$ 到第 $y$ 项这一子数列的平均数。
操作 $3$：`3 x y` ，表示求出第 $x$ 到第 $y$ 项这一子数列的方差。

关于方差：对于一个有 $n$ 项的数列 $A$，其方差 $s^2$ 定义如下：
$$s^2=\frac{1}{n}\sum _{i=1}^n{(A_i-\bar{A})}^2$$
其中 $\bar{A}$ 表示数列 $A$ 的平均数，$A_i$ 表示数列 $A$ 的第 $i$ 项。

$$s^2=\frac{1}{n}\sum _{i=1}^n{(A_i-\bar{A})}^2=\frac{1}{n}\sum _{i=1}^n(A_i^2-2A_i\bar{A}+{\bar{A}}^2)=\frac{1}{n}\sum _{i=1}^n{A}_i^2-\frac{2}{n}\sum _{i=1}^n{A}_i\bar{A}+\frac{1}{n}\sum _{i=1}^n{\bar{A}}^2$$

```cpp
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 2e5 + 9;

int n, m;
double a[maxn];

double sum[maxn << 2], tag[maxn << 2], sq[maxn << 2];

int ls(int x) {
return x << 1;
}

int rs(int x) {
return x << 1 | 1;
}

void pushup(int x) {
sum[x] = sum[ls(x)] + sum[rs(x)];
sq[x] = sq[ls(x)] + sq[rs(x)];
}

void add(int x, int l, int r, double k) {
sq[x] += 2 * k * sum[x] + k * k * (r - l + 1);
sum[x] += k * (r - l + 1);
tag[x] += k;
}

void pushdown(int x, int l, int r) {
int mid = (l + r) >> 1;
if (tag[x] != 0) {
add(ls(x), l, mid, tag[x]);
add(rs(x), mid + 1, r, tag[x]);
tag[x] = 0;
}
}

void build(int x, int l, int r) { // build(x, l, r) 当前节点编号为x，维护的区间[l,r]。
if (l == r) {
sum[x] = a[l];
sq[x] = a[l] * a[l];
return ;
}
int mid = (l + r) >> 1;
build(ls(x), l, mid);
build(rs(x), mid + 1, r);
pushup(x);
}

double querySum(int x, int l, int r, int L, int R) {
// x 当前节点的编号
// l, r 当前节点维护的区间
// L, R 询问的区间
if (L <= l && r <= R) return sum[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
double ret = 0;
if (L <= mid) ret += querySum(ls(x), l, mid, L, R);
if (mid < R) ret += querySum(rs(x), mid + 1, r, L, R);
return ret;
}

double querySq(int x, int l, int r, int L, int R) {
// x 当前节点的编号
// l, r 当前节点维护的区间
// L, R 询问的区间
if (L <= l && r <= R) return sq[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
double ret = 0;
if (L <= mid) ret += querySq(ls(x), l, mid, L, R);
if (mid < R) ret += querySq(rs(x), mid + 1, r, L, R);
return ret;
}

void intervalAdd(int x, int l, int r, int L, int R, double k) {
if (L <= l && r <= R) {
add(x, l, r, k);
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (L <= mid) intervalAdd(ls(x), l, mid, L, R, k);
if (mid < R) intervalAdd(rs(x), mid + 1, r, L, R, k);
pushup(x);
}

int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%lf", &a[i]);
build(1, 1, n);
while (m--) {
int opt;
scanf("%d", &opt);
int x, y;
scanf("%d %d", &x, &y);
if (opt == 1) {
double k;
scanf("%lf", &k);
intervalAdd(1, 1, n, x, y, k);
}
if (opt == 2) {
printf("%.4lf\n", querySum(1, 1, n, x, y) / (y - x + 1));
}
if (opt == 3) {
double avg = querySum(1, 1, n, x, y) / (y - x + 1);
double sq = querySq(1, 1, n, x, y) / (y - x + 1);
printf("%.4lf\n", sq - avg * avg);
}
}
return 0;
}
```

----

##### 例二

如题，已知一个数列，你需要进行下面三种操作：

- 将某区间每一个数乘上 $x$；
- 将某区间每一个数加上 $x$；
- 求出某区间每一个数的和。
- 思路：

增加了一个区间乘法，我们此时只需要思考怎么 pushdown 就行了。

我们之前的 lazytag 的表示方法是：把整个区间 $+k$。

那么我们现在增加了乘法之后就是：把整个区间 $\times k+t$，也就是我们需要维护两个懒标记：$k$ 和 $t$。

区间加法就是把加法标记t增加v，也就是（把整个区间 $\times k+(t+v)$）

区间乘法就是把乘法标记和加法标记都乘 $v$，也就是 $(\mathrm{把}\mathrm{整}\mathrm{个}\mathrm{区}\mathrm{间}\times k+t)\times v=(\mathrm{把}\mathrm{整}\mathrm{个}\mathrm{区}\mathrm{间})\times (k\times v)+(t\times v)$。

```cpp
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 1e5 + 9;

int n, q, m;
ll a[maxn];

ll sum[maxn << 2], tag1[maxn << 2], tag2[maxn << 2];

int ls(int x) {
return x << 1;
}

int rs(int x) {
return x << 1 | 1;
}

void pushup(int x) {
sum[x] = (sum[ls(x)] + sum[rs(x)]) % m;
}

void build(int x, int l, int r) {
tag1[x] = 0, tag2[x] = 1;
if (l == r) {
sum[x] = a[l] % m;
return ;
}
int mid = (l + r) >> 1;
build(ls(x), l, mid);
build(rs(x), mid + 1, r);
pushup(x);
}

void add(int x, int l, int r, ll k) {
(sum[x] += k * (r - l + 1) % m) %= m;
(tag1[x] += k % m) %= m;
}

void mul(int x, int l, int r, ll k) {
sum[x] = sum[x] * k % m;
tag1[x] = tag1[x] * k % m;
tag2[x] = tag2[x] * k % m;
}

void pushdown(int x, int l, int r) {
int mid = (l + r) >> 1;
if (tag2[x] != 1) {
mul(ls(x), l, mid, tag2[x]);
mul(rs(x), mid + 1, r, tag2[x]);
tag2[x] = 1;
}
if (tag1[x] != 0) {
add(ls(x), l, mid, tag1[x]);
add(rs(x), mid + 1, r, tag1[x]);
tag1[x] = 0;
}
}

void intervalAdd(int x, int l, int r, int L, int R, ll k) {
if (L <= l && r <= R) {
add(x, l, r, k);
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (L <= mid) intervalAdd(ls(x), l, mid, L, R, k);
if (mid < R) intervalAdd(rs(x), mid + 1, r, L, R, k);
pushup(x);
}

void intervalMul(int x, int l, int r, int L, int R, ll k) {
if (L <= l && r <= R) {
mul(x, l, r, k);
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (L <= mid) intervalMul(ls(x), l, mid, L, R, k);
if (mid < R) intervalMul(rs(x), mid + 1, r, L, R, k);
pushup(x);
}

ll querySum(int x, int l, int r, int L, int R) {
if (L <= l && r <= R) return sum[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
ll ret = 0;
if (L <= mid) ret += querySum(ls(x), l, mid, L, R);
if (mid < R) ret += querySum(rs(x), mid + 1, r, L, R);
return ret % m;
}

int main() {
scanf("%d %d %d", &n, &q, &m);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
while (q--) {
int opt; scanf("%d", &opt);
if (opt == 1) {
int x, y;
ll k;
scanf("%d %d %lld", &x, &y, &k);
intervalMul(1, 1, n, x, y, k);
}
if (opt == 2) {
int x, y;
ll k;
scanf("%d %d %lld", &x, &y, &k);
intervalAdd(1, 1, n, x, y, k);
}
if (opt == 3) {
int x, y;
scanf("%d %d", &x, &y);
printf("%lld\n", querySum(1, 1, n, x, y));
}
}
return 0;
}
```

 

----

##### 例三

$n$ 个数，$q$ 次操作。

操作 ```0 x y``` 把 $A_x$ 修改为 。

操作 ```1 l r``` 询问区间 $[l,r]$ 的最大子段和。

思路：

怎么求解区间最大子段和呢？我们的核心问题是解决 pushup。

首先，如果不跨越中间分界线，左右两边的最大子段和可以直接成为当前区间的最大子段和。

其次，如果跨越了中间分界线，那么左右两边的最大子段和可以直接由左边的最大后缀和和右边的最大前缀和拼起来。

而最大后缀和和最大前缀和也需要 pushup，它们的维护是简单的。

----

##### 例四

第一行一个整数 $n$，代表数列中数的个数。

第二行 $n$ 个正整数，表示初始状态下数列中的数。

第三行一个整数 $m$，表示有 $m$ 次操作。

接下来 $m$ 行每行三个整数 `k l r`。

- $k=0$ 表示给 $[l,r]$ 中的每个数开平方（下取整）。

- $k=1$ 表示询问 $[l,r]$ 中各个数的和。

**数据中有可能 $l>r$，所以遇到这种情况请交换 $l$ 和 $r$。**

思路：

发现一个很严重的问题：开平方这个操作，完全不能 pushdown。

观察：一个数不会被开很多次平方，$5$ 位数开至多 $4$ 次方就变成 $1$ 了。

因此我们的策略是：每次修改，看一下这个区间的最大值，如果小于等于 $1$，那么直接不动这个区间。如果大于 $1$，那么直接两边递归下去把它们一个一个改了。

复杂度是 $O(n\log n\log V)$。

----

### 树状数组

树状数组基本上是线段树的弱化但又快又好写版本。

维护一个比线段树更快的数据结构，支持对序列：

1. 单点加

2. 查询前缀和/前缀最大值。

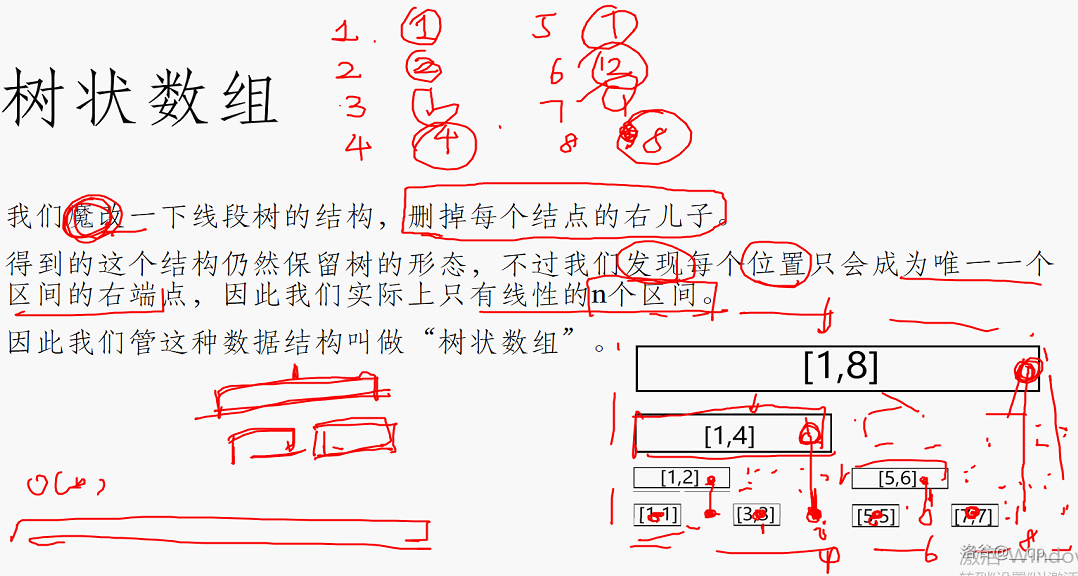
我们魔改一下线段树的结构，删掉每个结点的右儿子。

得到的这个结构仍然保留树的形态，不过我们发现每个位置只会成为唯一一个区间的右端点，因此我们实际上只有线性的 $n$ 个区间。

因此我们管这种数据结构叫做“树状数组”。


#### lowbit

观察：如果我们记 $\text{lowbit}(x)$ 表示数x二进制表示从右往前最低位的 $1$ 与它之前的所有 $0$ 构成的数，例如 $x=(101100{)}_2$，那么 $\text{lowbit}(x)=(100{)}_2$。

利用二进制补码的性质，我们可以得到 $\text{lowbit}(x)=x\mathrm{\&}(-x)$。

我们发现，树状数组的位置 $i$ 刚好维护了 $(i-\text{lowbit}(x),i]$ 这个长度为 $\text{lowbit}(x)$ 的区间。

因此我们只需要一个 for 循环就可以轻松维护出树状数组。

如图：


----

##### 例一

如题，已知一个数列，你需要进行下面两种操作：

1. 将某区间每一个数加上 $x$；

2. 求出某一个数的值。

思路：

普通的树状数组是单点加询问前缀和。

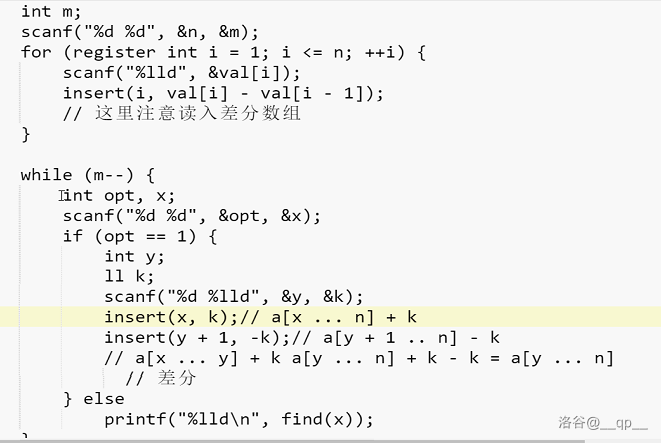
这个是区间加询问单点值。

只需要作一个差分就可以在这两个东西之间转化了。

```cpp
#include <bits/stdc++.h>

using namespace std;

const int maxn = 5e5 + 9;

inline int lowbit(int x) {
return x & (-x);
}

int n, m;
int sum[maxn]; // sum[i] 代表 以i为右端点的那个区间的和。

int query(int x) {
int ans = 0;
for (; x; x -= lowbit(x)) ans += sum[x];
return ans;
}

void add(int x, int k) {
for (; x <= n; x += lowbit(x)) sum[x] += k;
}
int qp[500005];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &qp[i]);
add(i, qp[i] - qp[i - 1]);
}
while (m--) {
int opt; scanf("%d", &opt);
if (opt == 1) {
int x, y, k;
scanf("%d %d %d", &x, &y, &k);
add(x, k);
add(y + 1, -k);
}
if (opt == 2) {
int x;
scanf("%d", &x);
printf("%d\n", query(x));
}
}
return 0;
}
```

##### 例二

树状数组，但是区间加，区间求和。

如果使用树状数组的话：

首先考虑维护差分数组d[i]

考虑：


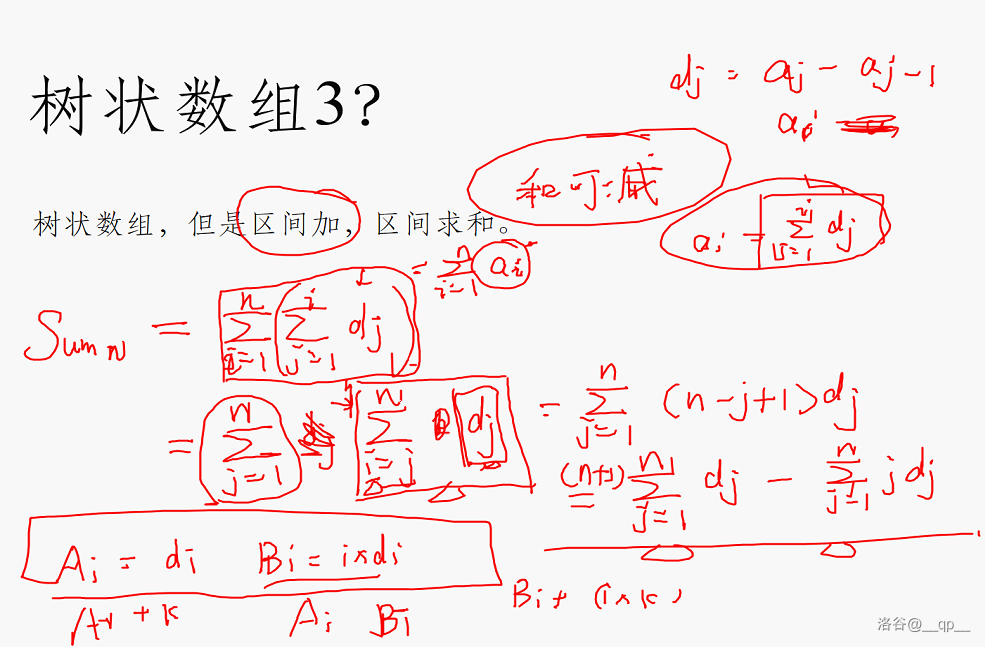
只需要维护 $d[j]$ 和 $j\times d[j]$ 两个树状数组即可。

----

### 二叉搜索树

维护一个数据结构，它是一个集合，支持：

1. 加入一个数（insert）
2. 删除一个数（delete）
3. 查询一个数的排名（rank，即比它小的数个数 $+1$）
4. 查询第k小数（k-th，即从小到大排序后第 $k$ 个位置上的数）
5. 查询一个数的前驱（pre）
6. 查询一个数的后继（suc）

你只需要一个平均复杂度 $O(\log n)$ 的算法，不需要保证最坏复杂度。

我们依然使用一棵二叉树去维护这个集合。

这棵二叉树需要满足：一个结点的权值，大于它左儿子的权值，小于它右儿子的权值，如果有相同权值，那么在这个结点的 $count$ 上 $+1$。

那么这个二叉树看上去就像是把一个排好序的数组“提起来”（换句话说，这个二叉树的中序遍历有序）

那么它为什么叫做“二叉搜索树”呢，因为这棵树可以非常方便地替我们完成“搜素一个值”这个任务。

从树根出发， 每次检查这个值与当前结点的权值的大小关系，如果相等那么找到了，否则如果值比当前结点小，那么向左走，不然向右走。复杂度 $O(\mathrm{树}\mathrm{高})$。

接下来我们开始分别实现这 $6$ 个功能：

1. 插入，从根开始，如果能搜素到这个值那么直接 $count++$，不然在搜素到的那个空位置新建一个结点存放这个值。
2. 删除，我们最好使用惰性删除，也就是把这个点删了但是这个空点还留在树上。
3. 查询一个数的排名，我们在二叉搜索树上查找这个数，如果下一步递归到右儿子，那么将排名增加 $sz[\mathrm{左}\mathrm{儿}\mathrm{子}]+count[\mathrm{当}\mathrm{前}\mathrm{点}]$，最后如果找到了，还需要加上 $sz[\mathrm{左}\mathrm{儿}\mathrm{子}]+1$。
4. 查询第 $k$ 小，我们同样在二叉搜索树上从根开始搜素，不过这次变成了：从根开始，如果 $k\le sz[\mathrm{左}\mathrm{儿}\mathrm{子}]$，那么向左儿子递归。如果 $0<k-sz[\mathrm{左}\mathrm{儿}\mathrm{子}]\le count[\mathrm{当}\mathrm{前}\mathrm{点}]$，那么当前点就是答案，否则把 $k$ 减去 $sz[\mathrm{左}\mathrm{儿}\mathrm{子}]+count[\mathrm{当}\mathrm{前}\mathrm{点}]$，然后向右递归。
5. 查询前驱，其实就是 $kth(rank(v)-1)$。
6. 查询后继，其实就是 $kth(rank(v+1))$。

-----

#### 二叉搜索树和线段树

其实二叉搜索树可以看成某种意义上的线段树，这意味着它可以承担一些区间操作的任务，也可以打懒标记。（比如 splay 和 fhqtreap 可以做的区间 reverse）

同理，线段树也可以视作一种二叉搜索树，这让它也可以维护一个集合。（动态开点权值线段树）

代码：

```cpp
#include <bits/stdc++.h>

// using std::cin;
// using std::cout;
namespace FastIO {

template<class T> inline void read(T &x) {
x = 0; bool f = 0; int ch = getchar();
for (; !isdigit(ch); f = (ch == '-'), ch = getchar()) ;
for (; isdigit(ch); x = x * 10 + ch - '0', ch = getchar()) ;
x = f ? -x : x;
}

inline int read() {
int x = 0; bool f = 0; int ch = getchar();
for (; !isdigit(ch); f = (ch == '-'), ch = getchar()) ;
for (; isdigit(ch); x = x * 10 + ch - 48, ch = getchar()) ;
return f ? -x : x;
}

int NUM[65];
template<class T> inline void Write(T x) {
if (x == 0) { putchar('0'); return ;}
if (x < 0) putchar('-');
x = x > 0 ? x : -x;
int tot = 0;
while (x) NUM[tot++] = x % 10 + 48, x /= 10;
while (tot) putchar(NUM[--tot]);
}

template<class T> inline void write(T x, char op) {
printf("%d\n", x);
}

}

using namespace FastIO;

const int MAX_N = 1e5;

int n;

int tot = 1;
int rt = 1, ch[MAX_N + 9][2], val[MAX_N + 9], sz[MAX_N + 9], cnt[MAX_N + 9];

void insert(int x) {
int u = rt, lst = 0;
for (; u && val[u] != x; lst = u, u = ch[u][x > val[u]]) sz[u]++;
if (val[u] == x) cnt[u]++, sz[u]++;
else {
if (lst) u = ch[lst][x > val[lst]] = ++tot;
val[u] = x;
cnt[u] = sz[u] = 1;
}
}

int rank(int x) {
int u = rt, res = 0;
for (; u && val[u] != x; u = ch[u][x > val[u]])
if (x > val[u]) res += sz[ch[u][0]] + cnt[u];
if (val[u] == x) res += sz[ch[u][0]];
return res + 1;
}

int kth(int k) {
int u = rt;
while (1) {
if (k <= sz[ch[u][0]]) u = ch[u][0];
else if (k <= sz[ch[u][0]] + cnt[u]) return val[u];
else k -= sz[ch[u][0]] + cnt[u], u = ch[u][1];
}
}

int pre(int x) {
return kth(rank(x) - 1);
}

int suc(int x) {
return kth(rank(x + 1));
}

void del(int x) {
int u = rt, lst = 0;
for (; val[u] != x; lst = u, u = ch[u][x > val[u]]) sz[u]--;
cnt[u]--, sz[u]--;
}

int main() {
read(n);
while (n--) {
int op = read(), x = read();
switch (op) {
case 1 : insert(x); break;
case 2 : del(x); break;
case 3 : write(rank(x), '\n'); break;
case 4 : write(kth(x), '\n'); break;
case 5 : write(pre(x), '\n'); break;
case 6 : write(suc(x), '\n'); break;
default : break;
}
}
return 0;
}
```

 

----

#### 平衡树

二叉搜索树最坏时间复杂度显然是 $O(n)$ 的，其原因在于这棵搜索树可以长得很不“平衡”，（最平衡的二叉树就是完全二叉树）

因此我们想出了各种奇奇怪怪的方法让二叉搜索树保持平衡，来让它能够真正达到 $O(\log n)$ 的时间复杂度。

这里给大家介绍一个非常简单但不是很实用的平衡树：替罪羊树。

它的思路很简单暴力：我们不平衡，那么我们每当整棵树不平衡到一个程度了，就把它整个推平重构成一棵完全二叉树。

这个所谓“不平衡到一个程度”，我们认为：其左或右儿子的大小 $>$ 整个子树大小的 $0.7$ 倍，或者删除的点的数量占整棵树的 $(1–0.7=0.3)$ 倍。

因为这个操作支持删除不是很容易，因此我们直接采用懒惰的方法，如果一个结点的 $count$ 为 $0$ 就把它留在那里不动它。

可以通过一些深刻的复杂度证明它的复杂度是 $O(n\log n)$的。

----

## 字符串算法

### 字符串

字符串当然就是由若干字符拼成的串。

关于字符串，我们讨论的其中一个就是字符串的“匹配”问题，也就是说，我给出两个字符串，你怎么知道其中一个串是另一个串的子串？它在多少地方出现了？这也是我们本次课研究的问题。其它的问题，我们会放到今后学习各种子串科技（后缀数组，后缀自动机，基本子串结构）的时候。

概念：

1. 字符集：就是字符串里所有字符构成的集合。
2. 子串：就是字符串的一个区间。
3. 前缀/后缀：就是字符串一个从 $1$ 开始的区间和一个以 $n$ 结尾的区间。

### 哈希

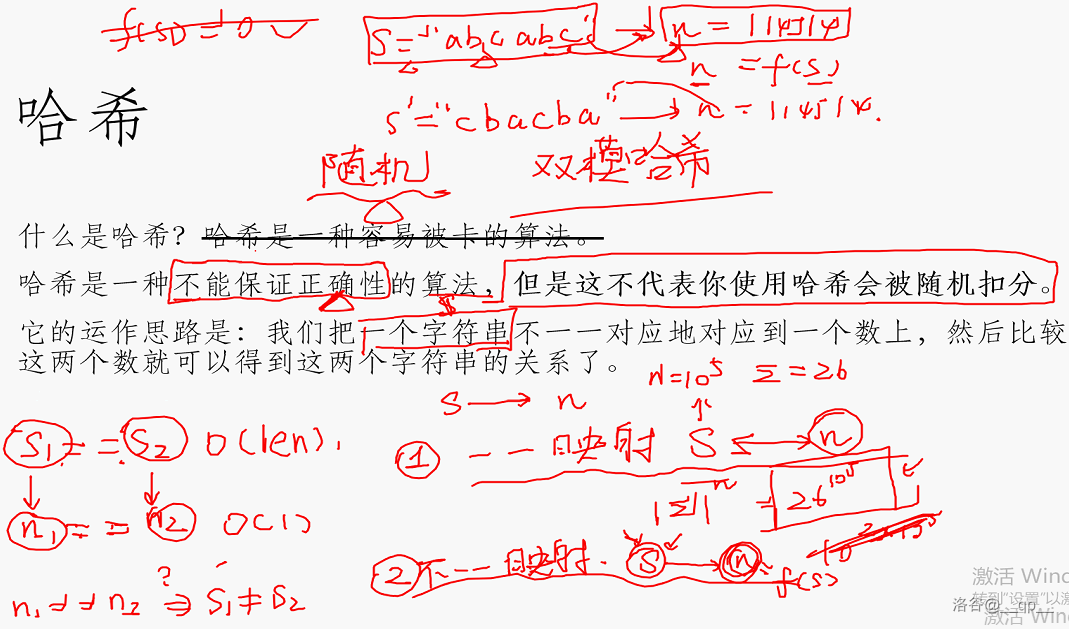
什么是哈希？哈希是一种容易被卡的算法。

哈希是一种不能保证正确性的算法，**但是这不代表你使用哈希会被随机扣分**。

它的运作思路是：我们把一个字符串不一一对应地对应到一个数上，然后比较这两个数就可以得到这两个字符串的关系了。

那么，怎么对应呢？


代码：

```cpp
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
inline long long read(){
long long v = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c = '-'){
f = -1;
}
c = getchar();
}
while(c >= '0' && c <= '9'){
v = v * 10 + c - '0';
c = getchar();
}
return v * f;
}
inline void print(long long x){
if(x < 0){
putchar('-');
x = -x;
}
if(x < 10){
putchar(x + '0');
} else {
print(x / 10);
putchar(x % 10 + '0');
}
}
const int maxn = 2e5 + 10;
const int b = 29, p = 1e9 + 7;
char s[maxn];
int hsh[maxn], base[maxn];//hsh[i]表示从1到i的前缀串
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> (s + 1);
int n = strlen(s + 1);
base[0] = 1;
for(int i = 1;i <= n;i++){
base[i] = 1ll * base[i - 1] * b % p;
}
for(int i = 1;i <= n;i++){
hsh[i] = ((1ll * hsh[i] * b % p) + (s[i] - 'a' + 1)) % p;
}
int l, r;
cin >> l >> r;
cout << (hsh[r] - 1ll * hsh[l - 1] * base[r - l + 1] % p + p) % p << '\n';
return 0;
}
```

 

我们使用这样一种哈希方法：

将整个字符串视为一个 $b$ 进制的数字对一个大质数 $p$ 取模得到的数字。

譬如，对于字符串 `s="abc"`，这种哈希值对应的结果就是 $1+2\times b+3\times b^2$。

其中 $b$ 和 $p$ 的值可以随便取，一般 $b$ 取 $29$ 或者 $31$，$p$ 取 ${10}^9+7$ 或者 $998244353$。

那么，两个相同字符串的哈希值显然是相同的。

更进一步地，我们可以轻松地求出这个字符串所有子串的哈希值。

$S,T$，求 $T$ 在 $S$ 的字串出现几次？

一个 $100000$ 长度的字符串，子串的个数将近 ${10}^{10}$，可是你的模数只有 ${10}^9$，这就意味着这个字符串几乎一定会出现两个不同的子串具有相同的哈希值，那么如果你比较这两个子串，就会得到错误的结果，也就是我们所说的“哈希冲突”。

某种意义上，哈希冲突是无法规避的。然而，这种冲突发生的概率非常微小（你不可能把所有 ${10}^{10}$ 个子串两两比较）。因此，我们期望它不会**在自然状态下**出现这种情况。

如果你不想让 OI 比赛的出题人人为地卡掉你的哈希，那么一个办法是使用不太常见的模数（比如 ${10}^9+33$，$1145141$），不过通常不会有毒瘤出题人会专门设计卡某一个特定哈希值的数据。（如果你遇到了，请狠狠攻击）

不过，一个更保险的方法是使用双值哈希。顾名思义，就是同时用两套模数 $b$ 和 $p$ 去计算哈希值，这样相当于有了一个双重保险。就几乎不可能出错了，被卡也很难。

双值代码：

```cpp
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
inline long long read(){
long long v = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c = '-'){
f = -1;
}
c = getchar();
}
while(c >= '0' && c <= '9'){
v = v * 10 + c - '0';
c = getchar();
}
return v * f;
}
inline void print(long long x){
if(x < 0){
putchar('-');
x = -x;
}
if(x < 10){
putchar(x + '0');
} else {
print(x / 10);
putchar(x % 10 + '0');
}
}
const int maxn = 2e5 + 10;
const int b1 = 29, p1 = 1e9 + 7;
const int b2 = 31, p2 = 998244353;
char s[maxn];
int hsh1[maxn], base1[maxn];//hsh[i]表示从1到i的前缀串
int hsh2[maxn], base2[maxn];
//int gethash1(int l, int r){
// return (hsh1[r] - 1ll * hsh1[l - 1] * base1[r - l + 1] % p1 + p1) % p1;
//}
//int gethash2(int l, int r){
// return (hsh2[r] - 1ll * hsh2[l - 1] * base2[r - l + 1] % p2 + p2) % p2;
//}
int gethash1(int l, int r){
return (hsh1[r] - 1ll * hsh1[l - 1] * base1[r - l + 1] % p1 + p1) % p1;
}
int gethash2(int l, int r){
return (hsh2[r] - 1ll * hsh2[l - 1] * base2[r - l + 1] % p2 + p2) % p2;
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
cin >> (s + 1);
int n = strlen(s + 1);
base1[0] = 1;
for(int i = 1;i <= n;i++){
base1[i] = 1ll * base1[i - 1] * b1 % p1;
}
base2[0] = 1;
for(int i = 1;i <= n;i++){
base2[i] = 1ll * base2[i - 1] * b2 % p2;
}
for(int i = 1;i <= n;i++){
hsh1[i] = ((1ll * hsh1[i] * b1 % p1) + (s[i] - 'a' + 1)) % p1;
}
for(int i = 1;i <= n;i++){
hsh2[i] = ((1ll * hsh2[i] * b2 % p2) + (s[i] - 'a' + 1)) % p2;
}
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if(gethash1(l1, r1) == gethash1(l2, r2) && gethash2(l1, r1) == gethash2(l2, r2)) cout << "Yes" << '\n';
else cout << "No" << '\n';
return 0;
}
```

#### 哈希表

维护一个数据结构，是一个集合，支持：

1. 插入一个（$\text{key},\text{value}$）对
2. 删除一个（$\text{key},\text{value}$）对
3. 查询一个 $\text{key}$ 对应的数是什么。

要求总共接近 $O(n)$ 地做完这些事情。

每一个字符串（$\text{value}$）有一个编号 $id$（$\text{key}$）。

先考虑 $\text{key}$ 的哈希值，就可以作为数组下标。 给插入的值对一个 ${10}^6$ 左右的数取模（${10}^6-3$）。把得到的数当作 $vis$ 的数组下标。

但因为这个数很小，所以很容易出现哈希冲突。

考虑是把这个 $vis$ 数组拓展成一个链表。每次插入一个数，如果发现这个数与其它的数哈希冲突了，就把它挂在先前的这个数后面。

这样就可以做到一个几乎线性的查询复杂度，显著优于同台竞争的线段树和平衡树。

下标为 $\text{long long}$ 的数组 $(xmodp,x)$ 可以避免哈希冲突。


----

##### 例一

Alice 和 Bob 最近热衷于玩一个游戏——积木小赛。

Alice 和 Bob 初始时各有 $n$ 块积木从左至右排成一排，每块积木都被标上了一个英文小写字母。

Alice 可以从自己的积木中丢掉任意多块（也可以不丢）；Bob 可以从自己的积木中丢掉最左边的一段连续的积木和最右边的一段连续的积木（也可以有一边不丢或者两边都不丢）。两人都不能丢掉自己所有的积木。然后 Alice 和 Bob 会分别将自己剩下的积木按原来的顺序重新排成一排。

Alice 和 Bob 都忙着去玩游戏了，于是想请你帮他们算一下，有多少种不同的情况下他们最后剩下的两排积木是相同的。

两排积木相同，当且仅当这两排积木块数相同且每一个位置上的字母都对应相同。

两种情况不同，当且仅当 Alice（或者 Bob）剩下的积木在两种情况中不同。

思路：

枚举 $B$ 剩下的子串的左端点 $l$，考虑让 $r$ 从 $l$ 到 $n$ 逐步扩展右端点。

那么我们只需要在 $A$ 串上，首先找到第一个为 $b[l]$ 的位置，然后再从 $b[l]$ 开始找它的下一个第一个为 $b[l+1]$ 的位置，以此类推，如果有一个位置匹配不上就让 `l++`。找下一个 $b$ 的过程可以维护一个 $c[i][j]$ 表示从点 $i$ 开始的第一个字母 $j$ 在哪个位置。然后在预处理的时候从后往前扫一遍 $A$ 串得到答案。

现在的问题是如何统计答案。由于字符串不能重复，我们需要每次将字符串的哈希值存下来，每次检查它与先前的哈希值是否相同。因此我们需要一个哈希表来完成这个事情。

-----

### Trie树

Trie树是一种像字典一样的二叉搜索树。

我们现在有很多字符串，怎么判断哪些字符串出现过，哪些字符串没有出现过呢？

我们考虑一本字典，如果我们想要在一个字典中找到某个单词，我们的做法是：首先找它的第一个字母，翻到指定页数后开始找第二个字母，如法炮制。

发现这个过程很像一棵树，因此我们可以模仿这个过程建一棵树，我们称为 trie 树。

显而易见地，对于一个小写字母字符集而言，trie 树的每个结点需要一个 `ch[][26]` 来存储它的 $26$ 个儿子，但是无论是插入还是查找都是 $O(len)$ 的。

----

##### 例一

```cpp
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
inline long long read(){
long long v = 0, f = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c = '-'){
f = -1;
}
c = getchar();
}
while(c >= '0' && c <= '9'){
v = v * 10 + c - '0';
c = getchar();
}
return v * f;
}
inline void print(long long x){
if(x < 0){
putchar('-');
x = -x;
}
if(x < 10){
putchar(x + '0');
} else {
print(x / 10);
putchar(x % 10 + '0');
}
}
int trans(char c){
if('a' <= c && c <= 'z') return c - 'a' + 1;
if('A' <= c && c <= 'Z') return c - 'A' + 27;
if('0' <= c && c <= '9') return c - '0' + 53;
}
const int maxn = 3e6 + 10;
int ch[maxn][63];
int tot = 1;//节点数
int sz[maxn];//点u子树中的单词数量
int tmp_len;//插入的字符串的长度
char tmp[maxn];//插入的字符串
void insert(){//把tmp insert到 trie 中
int u = 1;
sz[1]++;
for(int i = 1;i <= tmp_len;i++){
if(!ch[u][trans(tmp[i])]){
ch[u][trans(tmp[i])] += ++tot;
}
u = ch[u][trans(tmp[i])];
sz[u]++;
}
}
int query(){
int u = 1;
for(int i = 1;i <= tmp_len;i++){
if(!ch[u][trans(tmp[i])]){
return 0;
}
u = ch[u][trans(tmp[i])];
}
return sz[u];
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
int T;
cin >> T;
while(T--){
for(int i = 1;i <= tot;i++){
sz[i] = 0;
for(int j = 1;j <= 62;j++){
ch[i][j] = 0;
}
}
tot = 1;
int n, m;
cin >> n >> m;
for(int i = 1;i <= n;i++){
cin >> (tmp + 1);
tmp_len = strlen(tmp + 1);
insert();
}
for(int i = 1;i <= m;i++){
cin >> (tmp + 1);
tmp_len = strlen(tmp + 1);
cout << query() << '\n';
}
}
return 0;
}
```

----

#### 01trie

上面那个题其实给了我们一个提示：trie 不仅仅可以用来存储字符串，也可以用二进制的形式存储数！

因此我们瞬间得到了一个树高 $\log$ 值域的二叉搜索树！（当然，与一般的二叉搜索树略有不同）

Trie 瞬间就变得非常厉害了！

唯一的不足是花费的空间和时间是同阶的，都是 $O(n\log V)$，但是常数要比平衡树优秀很多，可以作为一个低配的平衡树使用。

----

##### 例一

您需要动态地维护一个可重集合 $M$，并且提供以下操作：

1. 向 $M$ 中插入一个数 $x$。
2. 从 $M$ 中删除一个数 $x$（若有多个相同的数，应只删除一个）。
3. 查询 $M$ 中有多少个数比 $x$ 小，并且将得到的答案加一。
4. 查询如果将 $M$ 从小到大排列后，排名位于第 $x$ 位的数。
5. 查询 $M$ 中 $x$ 的前驱（前驱定义为小于 $x$，且最大的数）。
6. 查询 $M$ 中 $x$ 的后继（后继定义为大于 $x$，且最小的数）。

对于操作 3,5,6，**不保证**当前可重集中存在数 $x$。

思路：

01trie 模板题，见代码。

需要注意的是，因为数可能有负数，我们需要给每个数加上一个很大的正整数让它变成一个正数。

-----

##### 例二

给定一棵 $n$ 个点的带权树，结点下标从 $1$ 开始到 $n$。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

观察：树上一条路径 $u$ 到v的异或和等于 $u$ 到根的异或和异或上 $v$ 到根的异或和，重叠的部分会抵消掉。

因此我们先求出每个点到根的异或和，它们构成一个集合 $S$。接下来只需要从 $S$ 中找出异或起来值最大的两个数即可。

考虑依次将 $S$ 中的每个数从高位到低位地插入 01trie，然后查询这个数和 trie 里面的哪个数异或起来差最大，方法是：

将这个数在 01trie上搜索。如果当前这一位是 $x$（$0$ 或 $1$），那么就尽可能走相反方向的结点，如果没有才走相同方向的结点。

1. 01trie 上子树异或一个数。

如果这一位是 $0$，不管；是 $1$，翻转这一位的左右儿子。

需要打一个懒标记。

2. 01trie 中的所有数整体 $+1$。

从低到高把所有数加入 01trie。

每次翻转左右儿子之后走左儿子。

-----

### KMP与Z函数

给定长一点的字符串 $S$（称为文本串）和短一点的字符串 $T$（称为模式串），求 $T$ 在 $S$ 中的哪些位置出现（找 $T$ 出现位置的开头位置）

要求 $O(|S|+|T|)$ 且不能使用哈希。

这个名字是三个人的首字母。

它涉及到一个比较深刻的东西，叫做 border。一个字符串 $s$ 的 border 是 $s$ 的一个子串 $s^{\prime }$，满足 $s^{\prime }$ 既是 $s$ 的前缀又是 $s$ 的后缀，且 $s^{\prime }$ 不是 $s$ 本身。（前面后面各有几对）

几个 border 的例子：

1. `s=‘abcabc’,s’ =‘abc`
2. `s=‘((())(’,s’=‘(’`

3. `s=‘aacaaa’,s’=‘a’`

最长的 border 是 $i$ 不代表 $i-1$ 是一个border。


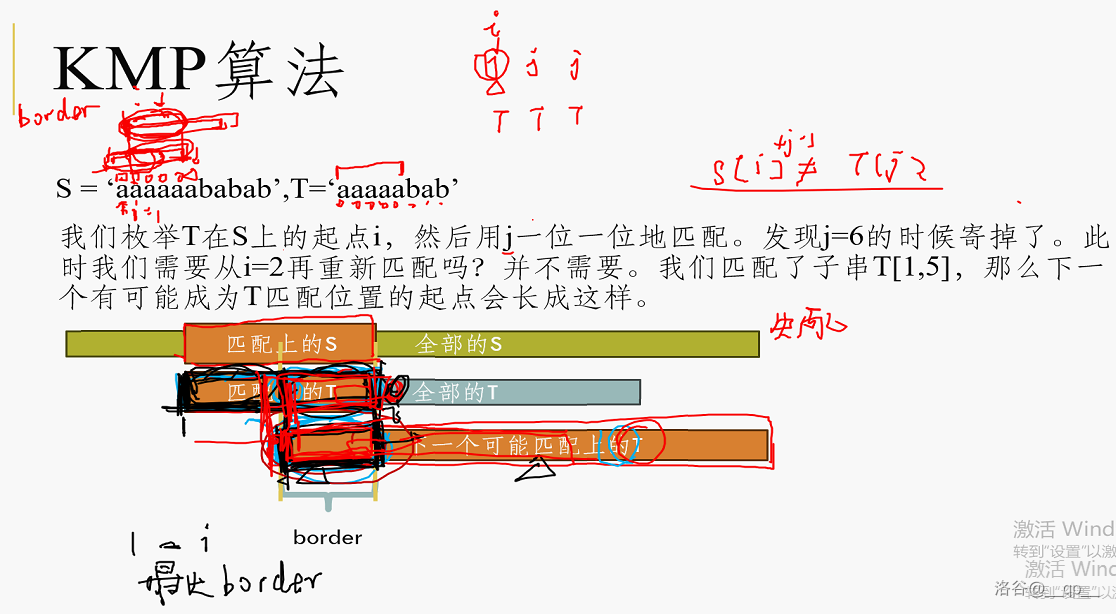
所以问题就很显然了。我们下一步并不需要从头开始，而只需要从 $T$ 的 border 位置开始即可。

那么我们的算法流程是：失配 $\to$ 跳 border $\to$ 再失配 $\to$ 再跳 border。

这样，我们每次在 $S$ 上移动一步，在 $T$ 上也移动了一步，border 最多增加 $1$，于是我们最多只会增加 $|S|$ 次 border，那么自然也最多回跳小于 $|S|$ 次 border，复杂度于是就是 $O(|S|+|T|)$。

因为这个跳 border 的操作有点像指示失配之后“下一个”位置在哪的数组，因此有人用 $nxt$ 数组表示 border。

怎么求最长 border？

说起来简单，因为我们用到的 border 不会超出 $i$，因此直接将 $T$ 和自己匹配即可。

具体来讲，我们可以依次求出每个位置的 border，因为我们每次要求 $border[i]$ 的时候，只需要比较 $T[border[i-1]+1]$ 和 $T[i]$ 是否相等即可，如果不相等，那么就是失配了，我们继续跳 border。

----

#### Z函数

我们仿照 KMP 求 border 的思路，考虑充分利用之前已经求出的 z-box。

记当前位置为 $i$，已经求出 $1\sim i-1$ 的 z-box。现在，我们记 $s[l,r]$ 为**右端点最靠右**的那个 z-box 对应的字符串，换句话说，$z[l]=r-l+1$，并且 $l+z[l]-1$ 最大。

现在，我们对当前的 $i$ 作分类讨论：

当 $i>r$，我们无能为力，暴力求出z[i]。

当 $i\le r$，我们了如指掌。这个时候我们实际上已经知道在 $[l,r]$ 里面 $z[i]$ 至少是 $z[i-l]$ 了。如果 $i+z[i-l]-1<r$，我们就可以令 $z[i]=z[i-l+1]$ 然后停了。不然，那就在 $r-i+14\mathrm{的}\mathrm{基}\mathrm{础}\mathrm{上}\mathrm{继}\mathrm{续}\mathrm{扩}\mathrm{展}$$z[i]$。

由于我们只有在增加r指针的时候才去扩展 $z[i]$，因此总复杂度 $O(n)$。

----
## 标准模板库（STL）

### 入门

#### 模板 template

像 `queue<int>` 中 `<int>` 的使用是 C++ 的一个语法，它的作用类似于我们学过的“通配符”，可以检测任何一种类型，甚至是你自己定义的结构体。

----

#### 容器 container

容器就是 STL 里的数据结构，是拿来存放数据的瓶瓶罐罐。

容器分为序列容器（vector，list，deque），关联容器（set，map）和其它容器（bitset）。

你可以简单理解为，数组，平衡树，和 bitset。

它们是一个个的 class（你可以把它们当作 struct 来用），怎么用？

`std::vector<int> vec;`

从左到右分别是命名空间（standard），容器名，模板参数，变量名。

然后你就获得了一个名叫 $\text{vec}$ 的，里面存放 `int` 类型的 vector 容器。

----

#### 迭代器 iterator

迭代器像是 STL 版本的指针，用来在容器的各个元素之间移动。

首先，我们造一个 iterator，

`std::vector<int>::iterator it;`

这一行从 `std::vector<int>` 这个类中找出它里面的一个类 iterator，用它定义了一个变量 $it$。

那么这个 $it$ 就可以在 vector 上乱转了，比如

`for (it = vec.begin(); it != vec.end(); it++) ...`

如果想要访问 iterator 指向的值，就需要使用 `*it`。

----

### vector

向量 vector，你可以把它当成一个可以延长的数组。它的延长方式是，每次将自己的存储空间加倍。

它支持：

1. 用下标访问一个位置，`vec[1]`，$O(1)$。

2. 在末尾删除或插入元素，`vec.push_back(1)`，$O(1)$。

3. 插入或删除一个元素：与到 vector 结尾的距离成线性 $O(n)$。`vec.clear()`，清空 vector 但**不清空内存**。

4. `vec.empty()`, 返回一个 `bool` 代表 vector 是否为空。

5. `vec.size()`,返回一个 `unsigned int` 代表vector的元素个数。

6. `vec.begin(), vec.end()`，返回一个迭代器代表 vector 的第一个位置与【最后一个位置的下一个位置】。

7. `vector.front(),vec.back()`，返回 vector 的第一个元素和最后一个元素。

8. `vec.front(),vec.back()`，返回 vector 的第一个元素和最后一个元素。

9. `vec.insert(it, val);`，在迭代器 $it$ 前插入值 $val$。插入后仅被插入点前的迭代器有效。返回这次插入/删除得到的迭代器。

10. `vec.resize(n);`，将 vector 大小设为 $n$，多余的直接扔掉，复杂度与原大小的差线性。

11. `vec.erase(it);`，删除迭代器所指的元素，其余同 insert。

12. `vec.reserve(n);`，将 vector 的存储空间设为 $n$，不改变其大小，不能用来减少存储空间。

13. `std::vector<int> vec(n);`，生成一个初始大小为 $n$ 的 vector，全是 $0$。

14. `std::vector<int> vec(n,val);`，生成一个初始大小为 $n$ 的 vector，全是 $val$。

15. `std::vector<int> vec = {1, 2, 3, 4};`，生成一个初始元素为 $\{1,2,3,4\}$ 的 vector。

16. `for (int v : vec) {}`，顺序遍历 vec 的每一个元素。

代码：

```cpp
#include <iostream>
#include <vector>
using namespace std;
int main(){
// 1. 用下标访问一个位置，vec[1]，O(1)
vector<int> vec = {10, 20, 30, 40};
cout << "vec[1]: " << vec[1] << '\n'; // 输出: 20

// 2. 在末尾删除或插入元素，vec.push_back(1)，O(1)
vec.push_back(50);
for (int v : vec) cout << v << " "; // 输出: 10 20 30 40 50
cout << '\n';

// 3. 插入或删除一个元素，vec.clear()，O(n)
vec.clear(); // 清空元素，但不清空内存
cout << "After clear(): size = " << vec.size() << '\n'; // 输出: size = 0

// 4. vec.empty(), 返回一个bool代表vector是否为空
cout << "Is vec empty? " << (vec.empty() ? "Yes" : "No") << '\n'; // 输出: Yes

// 5. vec.size(), 返回一个unsigned int 代表vector的元素个数
vec.push_back(10);
vec.push_back(20);
cout << "vec size: " << vec.size() << '\n'; // 输出: 2

// 6. vec.begin(), vec.end()，返回一个迭代器
auto it = vec.begin();
cout << "First element: " << *it << '\n'; // 输出: First element: 10
it = vec.end();
// cout << "End element: " << *it << '\n'; // 迭代器指向最后一个元素的下一个位置，不能解引用。

// 7. vector.front(), vector.back()，返回vector的第一个元素和最后一个元素
cout << "First element: " << vec.front() << '\n'; // 输出: First element: 10
cout << "Last element: " << vec.back() << '\n'; // 输出: Last element: 20

// 8. vec.front(), vec.back()，返回vector的第一个元素和最后一个元素 (重复)
cout << "First element again: " << vec.front() << '\n'; // 输出: First element again: 10
cout << "Last element again: " << vec.back() << '\n'; // 输出: Last element again: 20

// 9. vec.insert(it, val); 在迭代器it前插入值val
it = vec.begin();
vec.insert(it, 5);
for (int v : vec) cout << v << " "; // 输出: 5 10 20
cout << '\n';

// 10. vec.resize(n); 将vector大小设为n，多余的直接扔掉
vec.resize(4);
for (int v : vec) cout << v << " "; // 输出: 5 10 20
cout << '\n';

// 11. vec.erase(it); 删除迭代器所指的元素
it = vec.begin();
vec.erase(it); // 删除第一个元素
for (int v : vec) cout << v << " "; // 输出: 10 20
cout << '\n';

// 12. vec.reserve(n); 将vector的存储空间设为n，不改变其大小
vec.reserve(10); // 预留10个元素的空间，但不会改变vec的实际大小
cout << vec.capacity() << '\n'; // 输出: 10

// 13. vector<int> vec(n); 生成一个初始大小为n的vector，全是0
vector<int> vec1(5);
for (int v : vec1) cout << v << " "; // 输出: 0 0 0 0 0
cout << '\n';

// 14. vector<int> vec(n, val); 生成一个初始大小为n的vector，全是val
vector<int> vec2(3, 7);
for (int v : vec2) cout << v << " "; // 输出: 7 7 7
cout << '\n';

// 15. vector<int> vec = {1, 2, 3, 4}; 生成一个初始元素为{1, 2, 3, 4}的vector
vector<int> vec3 = {1, 2, 3, 4};
for (int v : vec3) cout << v << " "; // 输出: 1 2 3 4
cout << '\n';

// 16. for (int v : vec) {} 顺序遍历vec的每一个元素
for (int v : vec3) cout << v << " "; // 输出: 1 2 3 4
cout << '\n';

return 0;
}
```

 

----

##### string

std::string 是 C++ 风格的字符串，它几乎就是一个 `std::vector<char>`，具有 vector 的上述所有功能。

1. `s.append(6,’*’);`，向 $s$ 末尾添加 $6$ 个 $\ast$，返回 $\ast \text{this}$。
2. `s.append(str), s.append(str,n),`，向 $s$ 末尾添加 C 风格字符串 str，str的前 $n$ 个字符，如果 str 是另一个 std::string，后者代表从位置 $n$ 开始 append。

3. 用 $+$ 和 $+=$ 连接字符串。

4. `s.substr(pos, cnt)`，返回 $[pos,pos+cnt)$ 这一段子串，不输入 $cnt$ 就是到最后。

5. `std::stoi(s);`，把 $s$ 变成一个 `int` 类型的数，类似的还有 std::stoll，std::stod。

6. `std::to_string(x)`，把x变成一个字符串，支持 `int`，`longlong`，`double` 等。

```cpp
#include <iostream>
#include <string>
#include <cstdlib>
using namespace std;
int main(){
// 1. 使用append()方法向字符串s末尾添加6个'*'
string s = "Hello";
s.append(6, '*'); // 向s末尾添加6个'*'
cout << "After append(6, '*'): " << s << '\n';

// 2. 使用append()方法向字符串s末尾添加C风格字符串
string str = " World!";
s.append(str); // 向s末尾添加str
cout << "After append(str): " << s << '\n';

// 3. 使用append()方法向字符串s末尾添加部分C风格字符串
const char* cstr = " Example!";
s.append(cstr, 4); // 只添加cstr的前4个字符
cout << "After append(cstr, 4): " << s << '\n';

// 4. 使用+和+=连接字符串
string s1 = "Hello";
string s2 = " World";
s1 += s2; // 使用+=连接
cout << "After +=: " << s1 << '\n';

string s3 = "Hello" + s2; // 使用+连接
cout << "After +: " << s3 << '\n';

// 5. 使用substr()提取子串
string s4 = "Hello, C++!";
string sub = s4.substr(7, 3); // 提取从位置7开始的3个字符
cout << "After substr(7, 3): " << sub << '\n';

// 不输入count，则默认为直到字符串结束
sub = s4.substr(7);
cout << "After substr(7): " << sub << '\n';

// 6. 使用stoi转换字符串为int类型
string numm = "12345";
int num = stoi(numm); // 将字符串转为int
cout << "After stoi: " << num << '\n';

// 使用stoll转换字符串为long long类型
string l = "9876543210";
long long ll = stoll(l);
cout << "After stoll: " << ll << '\n';

// 使用stod转换字符串为double类型
string pii = "3.14159";
double pi = stod(pii);
cout << "After stod: " << pi << '\n';

// 7. 使用to_string将数值转换为字符串
int x = 42;
string intt = to_string(x); // 将int转换为字符串
cout << "After to_string(x): " << intt << '\n';

long long lx = 1234567890123456;
string lxx = to_string(lx); // 将long long转换为字符串
cout << "After to_string(large_x): " << lxx << '\n';

double y = 3.14;
string yy = to_string(y); // 将double转换为字符串
cout << "After to_string(y): " << yy << '\n';

return 0;
}

```

----

### queue,stack,deque

$\text{Tips}$ ：小心空间！

#### queue

queue 是我们常说的 FIFO 的队列。

它仅仅支持 `front(),back(),empty(),size()` 这种简单的功能。

还有 `push(x),pop()`，分别表示向队尾插入元素，向队头删除元素。

不支持迭代器。

#### stack

stack 是我们常说的 FILO 的栈。

它支持 `empty(),size(),push(),pop()` 这种显而易见的功能。

它还支持 `top()`，访问栈顶元素。

#### deque

deque 算是一个加强版的vector，支持向头尾插入/删除元素，并且这玩意访问下标的效率居然是O(1)的！（有点常数）

支持 `empty(),front(),front(), back(), begin(),end(),clear(),insert(),erase(),push_back(),push_front(),pop_back(),pop_front(),resize()` 这些和 vector 一样的东西。

queue 和 stack 是通过 deque 实现的。

另：在 NOI2022 中，有若干名选手在比赛中使用了 ${10}^6$个 deque，由于 deque 会在创建时分配 $4$ 个 `int` 的内存，因此造成了 MLE，DayT1 获得了 $0$ 分。

----

### 堆

### priority_queue

优先队列是基于 vector 的二叉堆，有了它我们就几乎可以不用手写二叉堆了！

它支持：

`top()` 访问堆顶元素，`empty(),size(),push()` 插入元素并维护堆，`pop()` 移除堆顶并维护堆。

这个 template 告诉我们，如果想要把它从大根堆变成小根堆，需要：

`priority_queue<int, vector<int>, greater<int> > q;` 其中 `greater<int>` 是一个函数对象，类似于 C 风格的函数指针。

代码（小根堆）：

```cpp
#include <iostream>
#include <queue>
using namespace std;
priority_queue<int, vector<int>, greater<int>> pq;
int main(){
pq.push(10);
pq.push(30);
pq.push(20);
pq.push(5);
while(!pq.empty()){
cout << pq.top() << ' ';
pq.pop();
}
return 0;
}
```

----

### set,map,unordered_map

#### set

集合set是一个功能很少的平衡树，功能基本都是logn的，但是因为STL封装的特性，速度不及手写，开了O2跑得还行，常用。

1. `std::set<int> s;` 声明一个名为 $s$ 的 set。
2. `s.insert(s); s.erase(s);` 将 $s$ 加入集合，剔除集合。注意集合具有互异性，两个相等的元素会被视为一个。
3. set支持 `begin(), end()`，它的迭代器左右移动是按照值从小到大的顺序遍历每一个结点的，换句话说每次 `++it`，它都会找到这个迭代器的后继结点。
4. `s.lower_bound(x);` 返回第一个值不小于 $x$ 的元素对应的迭代器，相当于二分。
5. `s.upper_bound(x);` 分会第一个值大于 $x$ 的元素对应的迭代器。
6. `s.count(x);` 返回元素 $x$ 的数量，只可能为 $0$ 或 $1$ 。
7. `s.find(x);`返回元素 $x$ 对应的迭代器，如果没有返回 `s.end();`。
8. `clear(), size(), empty()`，无需多言。

```cpp
#include <iostream>
#include <set>
using namespace std;
int main(){
set<int> s;
s.insert(10);
s.insert(20);
s.insert(15);
for (auto it = s.begin(); it != s.end(); ++it) {
cout << *it << " ";
}
cout << '\n';

// 查找元素
auto it = s.find(15);
if (it != s.end()) {
cout << "Found 15" << '\n';
}

// lower_bound 和 upper_bound
auto lb = s.lower_bound(15);
if (lb != s.end()) {
cout << "lower_bound(15): " << *lb << '\n';
}

auto ub = s.upper_bound(15);
if (ub != s.end()) {
cout << "upper_bound(15): " << *ub << '\n';
}

// 删除元素
s.erase(10);
for (auto it = s.begin(); it != s.end(); ++it) {
cout << *it << " ";
}
cout << '\n';

return 0;
}

```

#### <utility\>pair

值对 pair 这个东西，其实就是把两个变量打一个包放在一起，它几乎就是：

``Struct my_pair { int a; double b; } ;``

1. pair可以这样初始化： `pair<int, int> pr = {1, 2};`。
2. 一个更标准的方式是使用 `std::make_pair(a, b);` 函数，顾名思义，返回一个第一个元素是 $a$，第二个元素是 $b$ 的 pair。
3. `pr.first, pr.second;` 它的两个成员变量，代表第一个/第二个元素。

----

#### map

映射 map 在底层的实现其实几乎和set是一样的，大家可以把它当成一个下标不一定是非负整数的数组。它的实现原理是用set存pair。

1. `map<int, double> mp;` 声明一个存储着从 `int` 到 `double` 的映射。
2. `mp[2] = 3.3;` 将 mp 中 $2$ 对应的 `double` 改为 $3.3$，如果先前 $2$ 没有对应的数，那么新建一个 $2\to 3.3$ 的对应关系。
3. `mp.count(x);` 返回有 $x$ 这个键值的 pair 有几个。（ $0$ 或 $1$）
4. `mp.insert(make_pair(1,2));` 向 mp 中插入一个 $1\to 2$ 的对应关系，如果先前已经有 $1$ 的对应关系，这次插入失败。
5. `clear(), size(), empty()`，无需多言。

----

#### multiset/multimap

可重集合/可重映射。

顾名思义，就是在 set 和 map 的基础上，每个元素可以出现多次。

注意，multiset 和 multimap 的 erase 会杀掉所有与这个值相等的元素。如果只想杀掉一个，使用 find 函数找到任意一个该元素的迭代器it后，`s.erase(it);`。

----

#### unordered_map

C++ 内置的哈希表。

与 map 用法基本相同。

不推荐使用，建议手写。

----

### bitset

顾名思义，存储 bit 的定长数组。

1. 声明一个 `bitset<8> b;` 可以给它赋初值。

2. bitset 就像是一个很长很长的二进制数，它可以与其它二进制数或者 bitset 进行位运算。
3. 可以用 [] 访问其特定某一位。
4. `.all(), .any(), .none()` 表示是否所有位/存在位/没有位被设为 $1$。
5. `.count()` 返回 $1$ 的个数。
6. `size()` 返回大小，即 `bitset<n> b;` 的那个 $n$。
7. `.set()` 设置所有位为 $1$，$set(p)$ 将位置 $p$ 设为 $1$，`.set(p, x)` 将位置 $p$ 设为 $x$，`.reset()` 清空 bitset，`.reset(p)` 将位置 $p$ 设为 $0$。`.flip()` 将所有位异或 $1$，`.flip(p)` 将位置 $p$ 异或 $1$。
8. `.to_string(char zero = ‘0’, char one = ‘1’)`，返回一个 std::string，将 bitset 的值转换为一个字符串，其中 $0$ 的位置用变量 $zero$ 替换，$1$ 的位置用变量 $one$ 替换。
9. `.to_ulong(); .to_ullong();` 将值转换为 `unsigned long` 或者 `unsigned long long`，如果不能转换会报错。

bitset 所有操作的复杂度是 $O(n/w)$ 的，其中 $w=32$，也就是说 bitset 实际上做到了把一个 `int`，$4$ 个字节，$32$ 个 bit 的信息同时处理，因此可以加速某些运算。

另一方面，bitset 因为是有压位，其连续读写效率相当优秀，利用它代替 `bool` 数组有时候也能起到加速的作用。例如，大家都学过用埃氏筛法筛质数。利用 bitset 优化后埃氏筛法的速度要快于欧拉筛。（见oi-wiki）

----

##### 例一

一共有 $n$ 个数，第 $i$ 个数 $x_i$ 可以取 $[a_i,b_i]$ 中任意值。
设 $S=\sum {x_i}^2$，求 $S$ 种类数。

思路：

直接 dp，$f[i][j]$表示前 $i$ 个数凑出来平方和是 $j$ 是否可行，转移就是枚举 $k$ 在 $a[i]\sim b[i]$ 之间然后$f[i][j]|=f[i-1][j-k\times k]$

发现这是一个位运算操作，我们使用 bitset，先枚举 $i$ 和 $k$，然后对于所有的 $j$ 用 bitset 一次性拿下。

复杂度 $O(n^5/w)$。

----

### STL函数

#### swap

交换两个对象，可以是变量，可以是容器。

#### max/min

传入两个数 $a,b$，返回它们中较大的那一个/较小的那一个。

一般使用方法：`max(1, 2), \min(a,b);`。

特殊使用方法：`max(\{1,2,3,4,5\});`。

#### sort

将一列数排序。

1. `sort(a + 1, a + n + 1, cmp);` 将一个数组 $a[1,n]$ 排序，$\text{cmp}$ 是一个函数的名字，代表排序方式。
2. `bool cmp(int a, int b) { return a < b; }` 这个是从小到大排序，小于号改成大于号是从大到小排序，不要写成小于等于和大于等于。
3. sort 还可以对 vector 排序，方法是 `sort(vec.begin(), vec.end(), cmp);`。

复杂度 $O(n\log n)$。

#### unique

将一个序列相邻的元素去重，把重复元素扔到末尾，返回去重后数组的末尾位置的下一个位置的指针。

通常用法：`sort(a+1, a+n+1); n=unique(a+1,a+n+1)-a-1;`。

对 vector 去重：`vec.erase(unique(vec.begin(),vec.end()), vec.end())`。

复杂度 $O(n)$。

#### reverse

顾名思义，将一个序列头尾整个翻转。

比如把 $12345$ 反转为 $54321$。

可以翻转数组，vector，字符串。

复杂度 $O(n)$。

#### find

顺序查找值，返回指向这个值的指针/迭代器，返回第一个位置。

一般用法 `int p = find(a+1,a+n+1,114) – a;`。

#### lower_bound

对一个已经单调不降的序列进行二分，返回指向第一个大于等于 $x$ 的位置的指针。

一般用法 `int p = lowerbound(a+1,a+n+1,514) – a;`。

upper_bound同理，之前已经讲过。

#### next_permutation

给定一个排列，生成这个排列的下一个排列。

一般用法：枚举全排列用来打暴力：

#### nth-element

找出序列中第 $n$ 小的元素，然后重排整个序列，使其左边均为比它小的数，右边均为比它大的数。复杂度几乎是 $O(n)$ 的。

一般用法：`nth_element(a+1,a+k, a+n+1,cmp);` 代表找出序列中第 $k$ 小的元素。