CSP-S突破营day2

## 倍增&快速幂

### 快速幂

计算一个数 $a$ 的 $n$ 次幂，怎么办？

观察：如果要计算一个数的 $2^k$，只需要把它作 $k$ 次平方即可，因此实际上我们可以 $O(k)=O (\log n)$ 地计算出一个数的 $2^k$ 次方。

对于一般的数 $y$ 用预处理。

我们预处理出 $2^0$ 个 $a$ 相乘，$2^1$ 个 $a$ 相乘，…，一直到 $2^k$ 个 $a$ 相乘，使得 $2^k\ge 𝑛$，接下来我们只需要把 $n$ 分成若干个 $2$ 的幂次相加就行了…这也是背包里二进制分组的思想。复杂度显而易见是 $O(k+\log n)=O(\log n)$ 的。

##### 写法一：

```cpp
int ksm(int a, int b, int p){
int ret = 1;
for(;b;b >>= 1, a = (long long)a * a % p){
if(b & 1){
ret = (long long)ret * a % p;
}
}
return ret;
}
```

##### 写法二：

```cpp
int ksm(int a, int b, int p){
if(b == 0) return 1 % p;
if(b == 1) return a % p;
long long mem = ksm(a, b >> 1, p);
if(b & 1) return mem * mem % p * a % p;
return mem * mem % p;
}
```

好像还有一个光速幂，放张图。


------

### 矩阵快速幂

矩阵不满足交换律，满足分配律。

$$(AB)C=A(BC)$$
$$A(B +C)=AB+AC$$
$$(B+C)A=BA+CA$$

矩阵的乘法满足下属式子：

$$ c_i=\sum^m_{k=1}a_{i,k}\times b_{k,j}$$

#### 模板

给定 $n\times n$ 的矩阵 $A$，求 $A^k$。

特殊地，定义 $A^0$ 为单位矩阵 $I = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}$。

思路：

板子题建议手打。

```cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = 105;
const int MOD = 1e9 + 7;
struct Matrix{
ll a[MAXN][MAXN];
} p;
ll n,k;
Matrix operator*(Matrix x, Matrix y){
Matrix t;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
t.a[i][j] = 0;
}
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
for(int k = 1;k <= n;k++){
t.a[i][j] = (t.a[i][j] + x.a[i][k] * y.a[k][j]) % MOD;
}
}
}
return t;
}

Matrix qpow(Matrix a,ll k){
Matrix cnt;
for(int i = 1;i <= n;i++){
cnt.a[i][i] = 1;
}
while(k){
if(k & 1) cnt = cnt * a;
a = a * a;
k >>= 1;
}
return cnt;
}
int main(){
cin >> n >> k;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
cin >> p.a[i][j];
}
}
Matrix ans = qpow(p,k);
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
cout << ans.a[i][j] << ' ';
}
cout << '\n';
}
return 0;
}
```

##### 例题1：

求斐波那契数列的第 $n$ 项。

斐波那契数列：$f_0=f_1=1,f_n=f_{n−1}+f_{n−2},n\le 2$。

首先，把相邻两项拿出来，搞成一个 $2\times 1$ 矩阵。
接下来，利用矩阵乘法的定义凑出一个递推式出来。
最后，利用矩阵乘法的结合律，把这个柿子不断写下去。

发现得到了一个东西的若干次幂的形式，那么使用快速幂就可以 $O(\log n)$ 。

如图：

$$\begin{bmatrix} f_n \\ f_{n-1} \end{bmatrix}=\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} f_{n-1} \\ f_{n-2} \end{bmatrix}=\Big(\begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}\Big)^{n-1}\begin{bmatrix} f_{1} \\ f_{0} \end{bmatrix}$$

##### 例题2：

请计算以下数列的前 $n$ 项和对 $\text{mod}$ 取模的值：

$$f_0=a,f_1=b,f_2=c,f_n=pf_{n-1}+qf_{n-3}+2^n+(n+1)^2+fib_n$$

注意到：

$$S_{n-1}=S_{n-2}+f_{n-1},f_n=pf_{n-1}+qf_{n-3}+2^n+n^2+fib_n,fib_{n+1}=f_{n}+f_{n-1},2^{n+1}=2^n\times2,(n+1)^2=n^2+2n+1$$

$$\begin{bmatrix} S_{n-1} \\f_{n}\\ f_{n-1}\\ f_{n-2}\\ fib_{n+1}\\ fib_{n}\\ 2^{n+1}\\ (n+1)^2\\ n+1\\ 1 \end{bmatrix} = \begin{bmatrix} 1&1&0&0&0&0&0&0&0&0&\\0&p&0&q&1&0&1&1&0&0\\0&1&0&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0&0&0\\0&0&0&0&1&1&0&0&0&0\\0&0&0&0&1&0&0&0&0&0\\0&0&0&0&0&0&2&0&0&0\\0&0&0&0&0&0&0&1&2&1\\0&0&0&0&0&0&0&0&1&1\\0&0&0&0&0&0&0&0&0&1\end{bmatrix}\begin{bmatrix} S_{n-2} \\f_{n-1}\\ f_{n-2}\\ f_{n-3}\\ fib_{n}\\ fib_{n-1}\\ 2^{n}\\ n^2\\ n\\ 1 \end{bmatrix}$$

##### 例题3：

已知一个数列 $a$，它满足：

$$
a_x=
\begin{cases}
1 & x \in\{1,2,3\}\\
a_{x-1}+a_{x-3} & x \geq 4
\end{cases}
$$

求 $a$ 数列的第 $n$ 项对 $10^9+7$ 取余的值。

$$\begin{bmatrix} a_x \\ a_{x-1} \\ a_{x-2} \end{bmatrix}=\Big(\begin{bmatrix} 1 &0& 1 \\ 1 & 0&0\\0&1&0 \end{bmatrix}\Big)^{n-3}\begin{bmatrix} a_{x-1} \\ a_{x-2}\\a_{x-3} \end{bmatrix}$$

```cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;

const int MAXN = 5;
const int MOD = 1e9 + 7;
struct Matrix{
ll a[MAXN][MAXN];
} p;
ll n = 3,k;
Matrix operator*(Matrix x, Matrix y){
Matrix t;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
t.a[i][j] = 0;
}
}
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
for(int k = 1;k <= n;k++){
t.a[i][j] = (t.a[i][j] + x.a[i][k] * y.a[k][j]) % MOD;
}
}
}
return t;
}

Matrix qpow(Matrix a,ll k){
Matrix cnt;
memset(cnt.a, 0, sizeof(cnt.a));
for(int i = 1;i <= n;i++){
cnt.a[i][i] = 1;
}
while(k){
if(k & 1) cnt = cnt * a;
a = a * a;
k >>= 1;
}
return cnt;
}
int main(){
int t;
cin >> t;
while(t--){
ll n;
cin >> n;
if(n <= 3){
cout << 1 << '\n';
continue;
}
n -= 3;
p.a[1][1] = p.a[2][1] = p.a[3][2] = p.a[1][3] = 1;
Matrix ans = qpow(p, n);
cout << (ans.a[1][3] + ans.a[1][2] + ans.a[1][1]) % MOD << '\n';
}
return 0;
}
```

-----

### 倍增

快速幂干了一个什么事情？

1. 成**倍**的计算 $a$ 的幂次。
2. 让答案以 $2$ 的次幂为步长去**增**加。

实际上这也就是倍增算法在干的东西。

不过，不同的倍增算法可能在具体实现上还有所不同。

1. 倍增法可以替换二分法，有些时候比二分法更优秀。（但没二分好写）。
2. 倍增法预处理某些东西，然后用的时候加一加/减一减。
3. 使用二的指数幂去拼东西的思想可以应用到某些最优化问题中去，比如用最少的纸币面值去表示 $[0,2^k)$ 中的所有金额。
4. 倍增应用的前提是结合律（能拼）。

##### 例题1

给出一个长度为 $n$ 的环，第 $i$ 个位置有一个权值 $a[i]$ 和一个跳跃参数 $b[i]$ 。跳跃参数的意思是，如果当前在点i，那么一次跳跃会到达点 $(i-1+b[i])%n+1$。你需要回答 $q$ 个问题：第 $i$ 个问题是：从 $p[i]$ 这个点出发，连续跳跃 $k[i]$ 次，最终会到达哪个点？途中每一步跳跃所到达的点的点权之和是多少？

$n,q\le 10^5$

思路：

对于每个点 $i$ ，预处理出来这个点 $i$ 向后跳 $2^j$ 步得到的数组 $mv[i][j]$，那么 `mv[i][0]=(i-1+b[i])%n+1`，`mv[i][j]=mv[mv[i][j-1]][j-1]`，就可以让 $j$ 从小到大递推了。如果想要求出点权和的话，我们可以再开一个数组 $val[i][j]$，表示从点 $i$ 跳 $2^j$ 步后得到的点权和，转移：`val[i][0]=a[mv[i][0]], val[i][j]=val[i][j-1]+val[mv[i][j-1]][j-1];`

接下来只需要从 $p[i]$ 开始把 $k[i]$ 拼出来即可，这部分参考快速幂。

------

## 数据结构

顾名思义：存放**数据**的**结构**。

数组是不是数据结构？当然是。

为啥需要设计繁多的数据结构？为了更高效地维护数据的某些信息，比如最大值，最小值，某些数据的和，异或和，等等。另一方面，为了对数据进行封装，让我们不至于为了一个很简单的任务使用一个很复杂的结构。

通常情况下数据结构完成某一个操作的时间为 $\log n$，可以接受的范围是 $\sqrt{n}$，在一些毒瘤题或者卡常做法中会出现 $\sqrt{n} \log n$ 这种东西。

裸的数据结构题：你需要支持若干修改操作/查询操作。强制在线/可以离线。

不裸的数据结构题：给你一道题，它的一个核心是通过某个数据结构维护一个东西。

----

### 单调数据结构

#### 滑动窗口问题

##### 例题1

有一个长为 $n$ 的序列 $a$，以及一个大小为 $k$ 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

我们可以这样设计一个数据结构，支持：尾部加入一个元素，头部删除一个元素，查询数据结构内所有元素的最大值。

我们发现这个东西除了第三个功能，有点像一个队列。

那么怎么维护最大值呢？一个很严重的问题摆在我们面前：“删除”操作很头疼，因为你不能做到删掉一个数之后“复原”最大值，也就是说最大值不满足**可减性**。

此时就有两个思路：

1. 通过栈结构规避删除操作，对应分块做法与“双栈模拟队列”做法。

2. 继续发掘题目中有用的性质，对应“单调队列”做法。

#### 单调队列

我们考虑后一个思路。

一个不那么显而易见的观察是：当一个位置 $j$ 对应的数字 $a[j]$ 比新加入位置 $i$ 对应的数字 $a[i]$ 要小（准确来讲，不大）的话，那么 $a[j]$ 在今后永远不可能成为最大的数字。因为它会先 $i$ 一步被扔出窗口。

因此，我们的数据结构里的所有元素应该满足这样一个特征：所有元素从左到右单调递减，只有这样才能够满足数据结构中的每一个元素都是有用的，也就是说我们舍弃了那些没用的元素。

更进一步地，此时最左侧的元素就是最大值！

那么，怎么维护这种“单调”的结构呢？我们发现，只需要在每次在尾部加入一个位置 $i$ 的时候，不断地 ` pop` 掉尾部那些比它小的元素，直到下一个元素严格比它大，就可以把它加入到队尾了！

由于每个元素仍然只入队一次，出队一次，因此总复杂度仍然是 $O(n)$ 的。

如果我们把要解决的问题写出来，会发现它长成这个样子：

$$ans_i=\displaystyle\max_{j\ge i-k+1}\{a_j\}=\max_{f(i)\ge g(i)}\{h(j)\}$$

问题变成：给定三个数组 $f,g,h$，求数组 $ans$。

考虑把这个问题转化到滑动窗口问题。

把下标按 $f$ 从小到大排序，此时：

1. 如果 $g$ 单调不降，那么变成滑动窗口问题。$O(n)$

2. 否则，我们不要使用队头 `pop` 这个操作，而是直接二分找分界点。

#### 单调栈

给定一个序列，对于每个位置 $i$ 求出 $i$ 之后第一个大于 $a[i]$ 的元素 $a[j]$ 对应的下标 $j$。

我们仿照单调队列的思路，考虑剔除不需要的元素。

把这个过程看成是一个“站队”的过程，每个身高为 $a[i]$ 的人向右看，能看到的第一个人。

对于 $j<k$，如果 $a[j]>a[k]$，那么 $k$ 就被 $j$ 完全挡死啥也看不见了。

删掉这样的k，我们会得到一个从左到右单调递增的序列，每次向这个序列的最左侧增加一个 $a[]$，然后删掉被它挡死的所有元素。最后最左边的那个元素就是我们想要的。

由于每个元素最多会进栈一次，因此复杂度 $O(n)$。

```cpp
for (int i = n; i >= 1; i--) {
while (top && a[i] >= a[stk[top]]) --top;
if (top) nxt[i] = stk[top];
stk[++top] = i;
}
```

 

----

### 堆

存集合的最值。

维护一个数据结构，维护一个集合，支持插入一个元素，查询最大值，删除最大值。

又遇到了删除问题，但是这次我们没有很好的性质去利用了，必须要使用更加复杂的数据结构。

考虑将数据结构中的每个元素排成一棵完全二叉树，使得父亲结点的值大于等于两个儿子结点的值，那么最大值就是根结点的值。

现在考虑如何实现插入和删除两个操作。


 

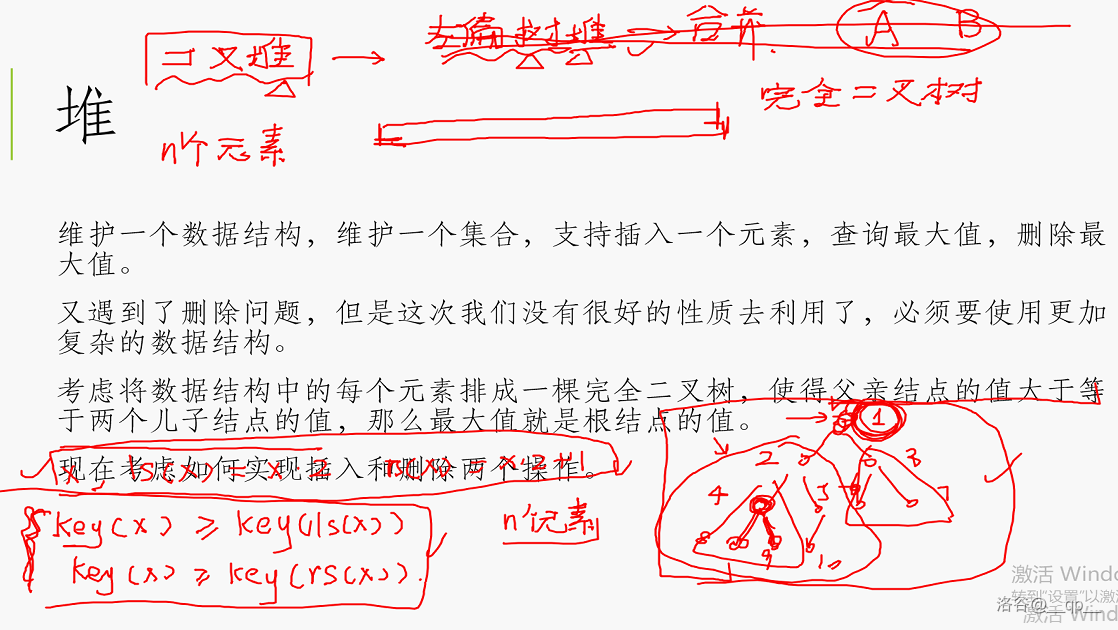
首先是插入：我们先把待插入的结点放在完全二叉树最后一层最右边的叶子之后。然后不断地向上将这个叶子与父亲结点 `swap`，直到父亲的权值大于等于这个叶子的权值。复杂度 $O(\log n)$。

接下来考虑删除：我们把最后一层的最后一个叶子节点与根交换，删除根节点，紧接着不停地把这个叶子与它权值最大的那个儿子 `swap`，重复这个过程直到不需要 `swap`。复杂度 $O(\log n)$。

我们称第一个过程中让新节点不断上浮的过程为“向上调整”，下面那个将叶子节点不断下沉的过程叫“向下调整”。

最后是直接用 $n$ 个元素建堆的方法：直接 `sort` 或者一个一个插入是 $O(n\log n)$ 的，但是我们从 $n$ 到 $1$ 不断向下调整每个结点，就是 $O(n)$ 的。

#### 考虑更多功能（可删除堆）

##### 例题1

维护一个数据结构，支持插入一个元素，删除**一个**值为 $v$ 的元素，查询最大值，删除最大值。

##### 例题2

给定一个长度为 $N$ 的非负整数序列 $A$，对于前奇数项求中位数。

找到并删除一个非堆顶元素太麻烦了！因此我们不妨“懒”一点：新开一个堆，维护所有“删除操作”，就像一个代办清单，那么堆顶的操作是最迫切的那个：元素值最大的那个。

接着，由于我们所有的操作都是在堆顶完成的，因此我们一旦看见堆顶的值刚好和我们“待办清单”中的第一个值一样，我们就把它和这个操作同时删掉。这样一来，我们既不用费劲去找那些值，只需要等它们自己到堆顶就行。

```cpp
priority_queue<int> heap, list;

void push(int x) {
heap.push(x);
}

void erase(int x) {
list.push(x);
}

int size() {
return heap.size() - list.size();
}

void check() {
while (heap.size() && list.size() && heap.top() == list.top())
heap.pop(), list.pop();
}

void pop() {
check();
heap.pop();
}

int top() {
check();
return heap.top();
}
```

----

#### 对顶堆

我们维护两个堆，然后把它们的堆顶拼在一起。

左边是一个大根堆，堆顶叫 $x$，右边是一个小根堆，堆顶叫 $y$。

我们需要满足 $x < y$。

每次加入一个元素 $v$，如果 $x < v$，那么我们把它扔进右面的小根堆，不然我们把它扔进左边的大根堆。

接下来，不停地把右边的堆顶扔进左边或者把左边的堆顶扔进右边：总之，让两个堆的大小差值**不超过 $1$ **。

最后堆大小较大的那个堆的堆顶就是中位数。（相当于我们把中位数夹在两个数中间）


##### 例题1

有两个长度为 $N$ 的**单调不降**序列 $A,B$，在 $A,B$ 中各取一个数相加可以得到 $N^2$ 个和，求这 $N^2$ 个和中最小的 $N$ 个。

思路：

考虑每一个 $a[i]+b[j]$，我们固定 $i$ 考虑每一个 $j$。

比如说 $n=5$，那么我们想要取出 $a[i]+b[4]$，就必须要先取 $a[i]+b[5]$，因为后者是更大的。

因此我们维护一个大根堆，一开始把每个 $a[i]+b[n]$ 丢进去，每次取出来一个之后就把 $a[i]+b[n-1]$ 重新丢进去，以此类推。

核心代码：

```cpp
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
int x=a[i]+b[j];
if(q.size()<n){
q.push(x);
}
else{
if(x<q.top()){
q.pop();
q.push(x);
}
else{
break;
}
}
}
}
int cnt=0;
while(q.size()){
c[++cnt]=q.top();
q.pop();
}
```

 

### 并查集

维护一个数据结构：一开始有 $n$ 个元素，分别位于 $n$ 个不同的集合，支持两个操作：

1. 将两个集合合**并**为一个集合。
2. **查**询两个元素是否在同一个集合中。

我们考虑用一个树形（准确来讲，森林）结构去实现这些操作。

把元素当成一个结点，并给每个点指派一个父亲结点，或者把它作为一个树根，此时它的父亲结点设为自己。

这样我们就可以把一个集合看成一棵有根树，它的根就是这个集合的代表元素。

查询两个点是否在一个集合其实就是查询两个点所在树的树根是否一样。

合并两个集合其实就是把其中一棵树的树根合并到另一棵树上。

单次查询是 $O(树高)=O(n)$ 的，合并因为要查询，所以也是 $O(树高)=O(n)$ 的。

```cpp
int find(int x){
if(x == fa[x]) return x;
return find(fa[x]);
}
```

#### 路径压缩与按秩合并

我们延续搜索中“记忆化”的思想，如果我们已经知道某个点的树根了，那我们直接把这个点的父亲设置为它的树根，这样以后再找根就只需要蹦一步了。

另一个优化是，如果我们每次把深度较小的那个树合并到深度较大的树上，就可以使得树高增加地尽可能缓慢。这样也可以减少时间复杂度。

```cpp
const int MAXN = 1e4 + 10;
int fa[MAXN], rk[MAXN];
int find(int x){
if(x == fa[x]) return x;
return fa[x] = find(fa[x]);//路径压缩
}
void merge(int x, int y){
x = find(x), y = find(y);
if(x == y) return ;
if(rk[x] > rk[y]){
fa[y] = x;
}
else if(rk[x] < rk[y]){
fa[x] = y;
} else {
fa[x] = y;
rk[y]++;
}
}
int main(){
cin.tie(0) -> sync_with_stdio(0);
int n;
cin >> n;
for(int i = 1;i <= n;i++){
fa[i] = i, rk[i] = 1;
}
return 0;
}
```

#### 时间复杂度

$O(α(n))$,可以认为是常数级别。

##### 例一

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成 $30000$ 列，每列依次编号为 $1, 2,\ldots ,30000$。之后，他把自己的战舰也依次编号为 $1, 2, \ldots , 30000$，让第 $i$ 号战舰处于第 $i$ 列，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为 `M i j`，含义为第 $i$ 号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第 $j$ 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：`C i j`。该指令意思是，询问电脑，杨威利的第 $i$ 号战舰与第 $j$ 号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

第二个操作意味着我们需要询问两个战舰的位置，但是并查集的结构是随时在改变的，因此我们需要一些别的技巧：

考虑对于每个点，记 $dep[u]$ 表示点u到它父亲的**实际**距离。特别地，如果一个点是树根，那么 `dep[x] = 0`。

这样一来，只要我们通过路径压缩把 $dep[x]$ 改为到根的距离 ，那么我们可以根据 `abs(dep[x] – dep[y] – 1)` 得到两个战舰之间的距离。

在路径压缩中，更新 $dep$ 是简单的：只需要把自己原本的 `dep[x]+=dep[fa[x]]` 即可。

这种父子边有边权的并查集称为“带权并查集”。

----

### 线段树

#### 区间问题

维护一个序列上的数据结构，支持：

1. 给某个位置加上一个整数。
2. 查询某个区间的和/最大值。

感受一下这个东西的难度，非常困难。

这个时候我们的分治结构要出来发挥神力了。

采取这种从中间对半劈开的方法，我们发现任何一个区间都可以表示成这些区间没有交集的并。

比如 $[2,6]$ 就是 $[2,2] + [3,4] + [5,6]$。

$$sum(x)=sum(ls(x))+sum(rs(x))$$

我们发现这样的对半分的区间实际上形成了一棵完全二叉树，称为线段树。

观察：一段区间在线段树上表现为一个被二进制拆分的前缀和一个被二进制拆分的后缀，因此一个区间总可以被划分为 $O(\log n)$ 个小区间。

这样我们只需要维护这 $O(n)$ 个区间上的和与最大值即可。

而修改一个点最多只会影响 $O(\log n)$ 个区间的值，我们直接修改这些区间即可。

复杂度：建树 $O(n)$，单次区间查询 $O(\log n)$，单点修改 $O(\log n)$。

```cpp
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int maxn = 2e5 + 9;

int n, m, a[maxn];

ll sum[maxn << 1], mx[maxn << 1], tag[maxn << 1];

int ls(int x) {
return x << 1;
}

int rs(int x) {
return x << 1 | 1;
}

void pushup(int x) {
sum[x] = sum[ls(x)] + sum[rs(x)];
mx[x] = max(mx[ls(x)], mx[rs(x)]);
}

void add(int x, int l, int r, ll k) {
sum[x] += k * (r - l + 1);
mx[x] += k;
tag[x] += k;
}

void pushdown(int x, int l, int r) {
int mid = (l + r) >> 1;
if (tag[x] != 0) {
add(ls(x), l, mid, tag[x]);
add(rs(x), mid + 1, r, tag[x]);
tag[x] = 0;
}
}

void build(int x, int l, int r) { // build(x, l, r) 当前节点编号为x，维护的区间[l,r]。
if (l == r) {
sum[x] = mx[x] = a[l];
return ;
}
int mid = (l + r) >> 1;
build(ls(x), l, mid);
build(rs(x), mid + 1, r);
pushup(x);
}

ll querySum(int x, int l, int r, int L, int R) {
// x 当前节点的编号
// l, r 当前节点维护的区间
// L, R 询问的区间
if (L <= l && r <= R) return sum[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
ll ret = 0;
if (L <= mid) ret += querySum(ls(x), l, mid, L, R);
if (mid < R) ret += querySum(rs(x), mid + 1, r, L, R);
return ret;
}

ll queryMax(int x, int l, int r, int L, int R) {
// x 当前节点的编号
// l, r 当前节点维护的区间
// L, R 询问的区间
if (L <= l && r <= R) return mx[x];
pushdown(x, l, r);
int mid = (l + r) >> 1;
ll ret = -2e9;
if (L <= mid) ret = max(ret, queryMax(ls(x), l, mid, L, R));
if (mid < R) ret = max(ret, queryMax(rs(x), mid + 1, r, L, R));
return ret;
}

void posAdd(int x, int l, int r, int p, ll k) {
if (l == r) {
sum[x] += k;
mx[x] += k;
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (p <= mid) posAdd(ls(x), l, mid, p, k);
else posAdd(rs(x), mid + 1, r, p, k);
pushup(x);
}

void intervalAdd(int x, int l, int r, int L, int R, ll k) {
if (L <= l && r <= R) {
add(x, l, r, k);
return ;
}
pushdown(x, l, r);
int mid = (l + r) >> 1;
if (L <= mid) intervalAdd(ls(x), l, mid, L, R, k);
if (mid < R) intervalAdd(rs(x), mid + 1, r, L, R, k);
pushup(x);
}

int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
build(1, 1, n);
while (m--) {
int opt; cin >> opt;
int x, y; cin >> x >> y;
if (opt == 1) {
int k;
cin >> k;
intervalAdd(1, 1, n, x, y, k);
}
if (opt == 2) {
printf("%lld\n", querySum(1, 1, n, x, y));
}
}
return 0;
}
```

#### 懒标记

如果区间加一个数呢？

我们发现，一次区间修改可能会影响所有的结点…

但是不要怕，我们要充分利用线段树的结构，把要修改的区间同样劈成 $O(\log n)$ 个区间，能不能只修改这几个区间？

懒标记：我们发现这个区间的答案是好办的：区间的和增加 $v\times (r-l+1)$，区间的最大值增加 $v$。因此我们先增加区间的答案，然后给这个区间做一个记号：设置一个 $tag[]$ 记录这个结点总共被加了多少。

那么当我们需要用到它子节点的时候，将标记“下传”到子节点，同时更新子节点的答案，这样懒标记就被下放到子节点继续挂着。

于是我们发现，只需要每次在前往子节点时下传懒标记，就可以使得每个结点的值都是正确的，我们也就完成了 $O(\log n)$ 的区间加。

----

### ST表

回忆倍增算法。

维护一个数据结构，支持查询任意区间的最大值。（RMQ问题）

在每一个位置i维护区间 $[i,i+2^k)$ 的最大值。

查询就拼起来。

查询有没有更快的做法？

直接叠起来！

预处理 $O(n\log n)$，查询 $O(1)$。

##### 例一

现在请求你维护一个数列，要求提供以下两种操作：

1. 查询操作。

语法：`Q L`

功能：查询当前数列中末尾 $L$ 个数中的最大的数，并输出这个数的值。

限制：$L$ 不超过当前数列的长度。$(L > 0)$

2. 插入操作。

语法：`A n`

功能：将 $n$ 加上 $t$，其中 $t$ 是最近一次查询操作的答案（如果还未执行过查询操作，则 $t=0$），并将所得结果对一个固定的常数 $D$ 取模，将所得答案插入到数列的末尾。

限制：$n$ 是整数（可能为负数）并且在长整范围内。

注意：初始时数列是空的，没有一个数。

思路：

倒着维护一个 ST 表。