24暑假集训day6上午&下午
DP
概念
状态、转移方程、初始化
先放一张图(相信都能理解:状态、转移方程、初始化的含义,随便引入斐波那契数列的题)
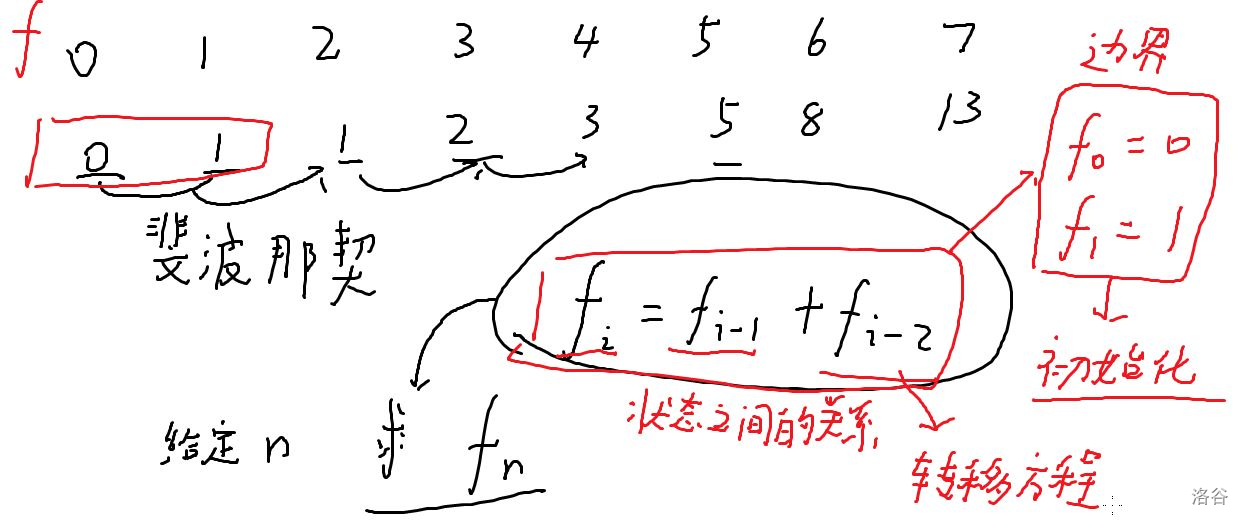
入门题
Problem 1
斐波那契数列
组合数
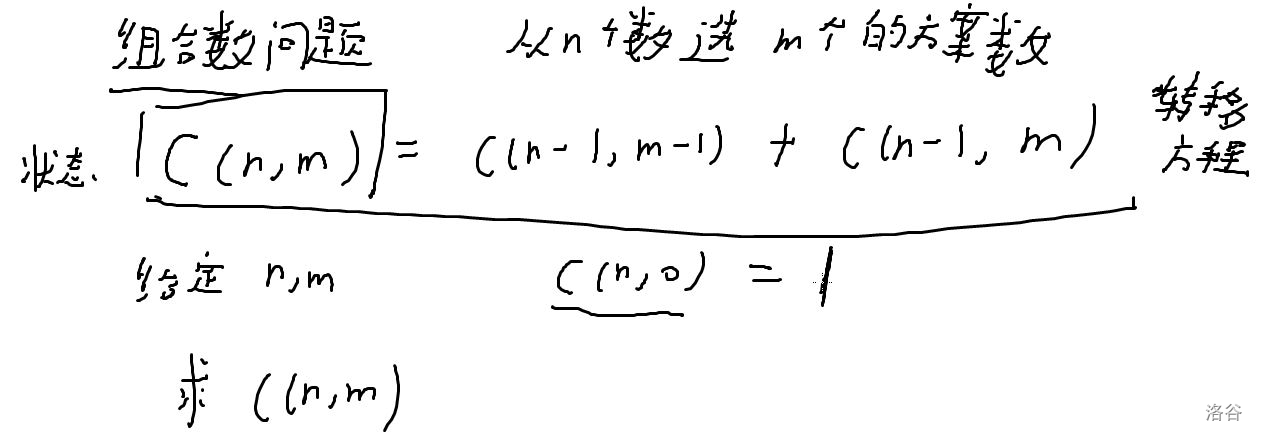
转移方程:
杨辉三角:
Problem 2
\(N\cdot M\)的方格图只能向右或者向下求走到右下的方案数?
和走到右下的最小代价?
Problem 3
数字三角形给你一个三角形,问从怎么走能够取得最大代价
Problem 4
在上一个题的基础上变化为求和 \(\bmod100\)之后最大的结果
多一个条件
多一维状态
Problem 5
最长上升子序列求方案
dp 状态的判定
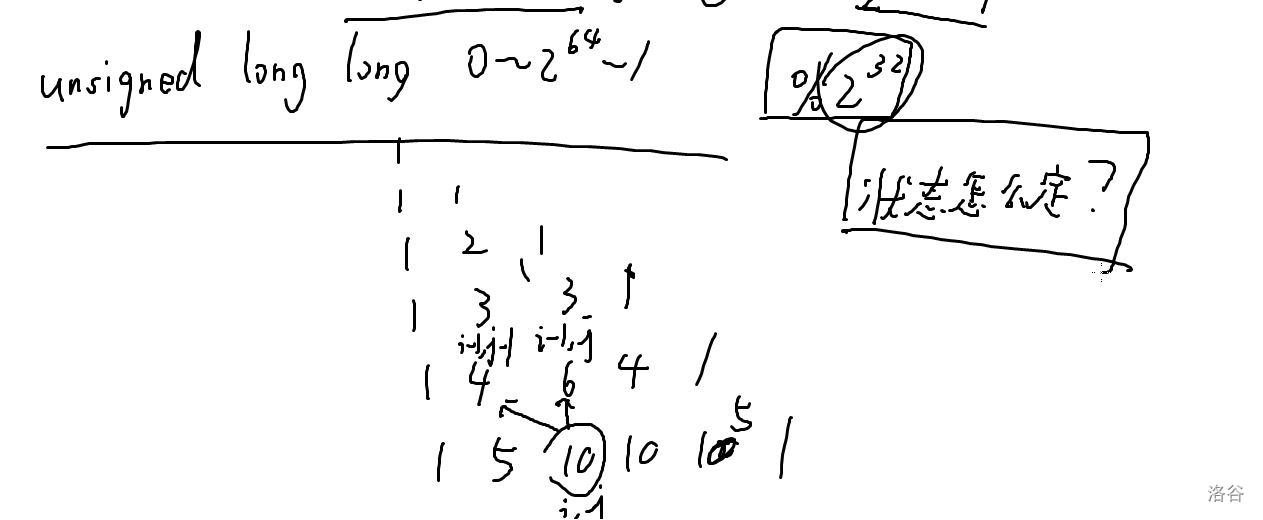
思考什么东西发生变化
\(f[\)位置\(][\)和\(]\implies f[i][j][k]\) 是否可能
走到 \((i, k)\) 和为 \(k\)
int f[位置] = 和
\(f[i][j]\) 走到 \((i, k)\) 和最大是多少
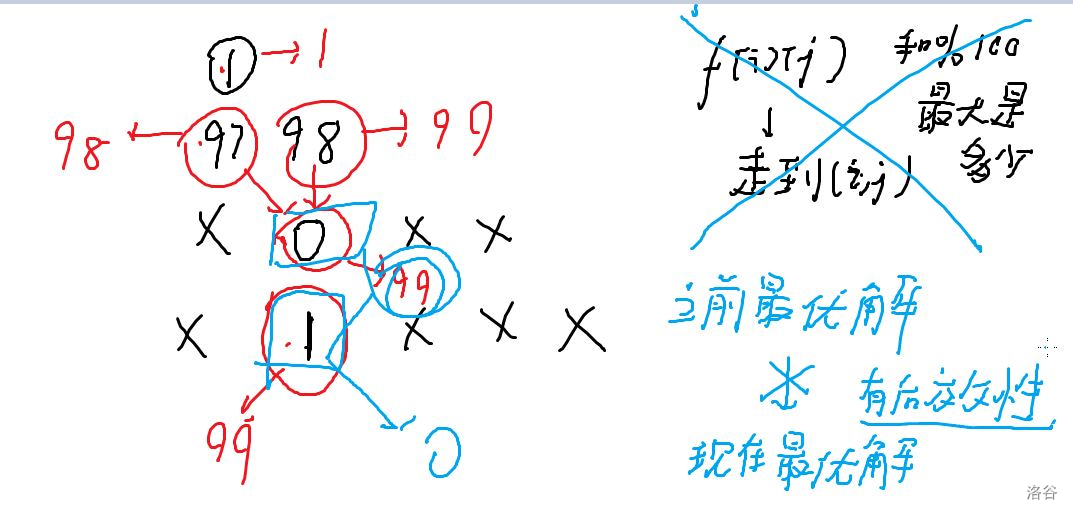
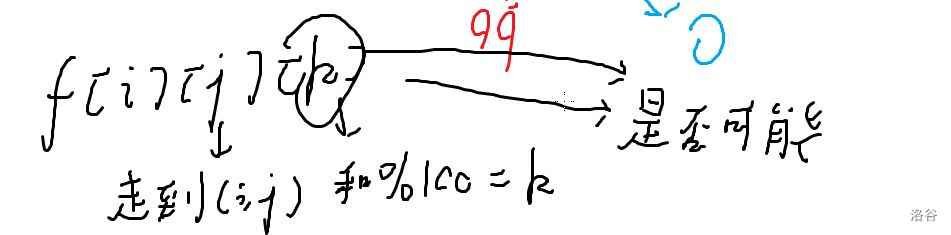
Problem 6
滑雪 \(N\) 行 \(M\) 列的图
- 每个格子有高度
- 可以滑向周围四个比自己矮的格子
- 最多能划多远
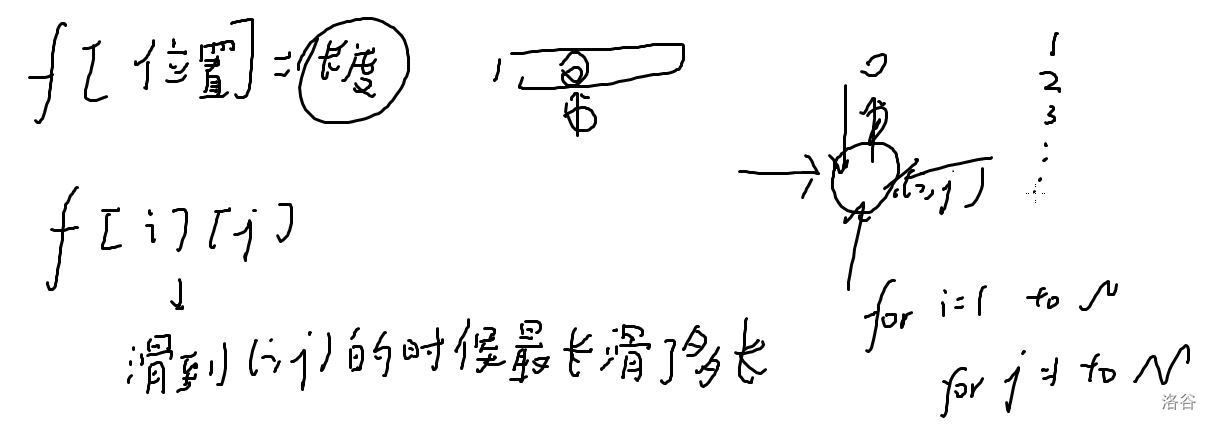
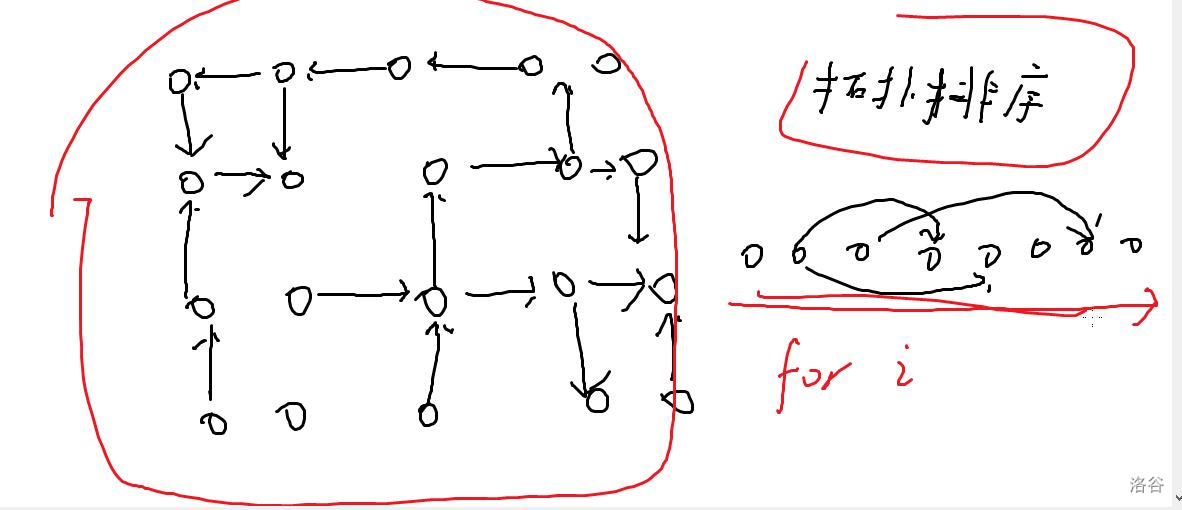
思路:
排序之后就是前面一道题
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
const int MAXX = 1e5 + 10, MAXN = 1e9 + 10;
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n, m;
int h[233][233], f[233][233];//f[i][j]代表从(i, j)这个位置出发 最远能滑多远
bool g[233][233];//g[i][j]代表f[i][j]算过没
int dx[10] = {-1, 1, 0, 0};//上下左右
int dy[10] = {0, 0, -1, 1};//dx[i], dy[i]代表的是在第i个方向下x的坐标和y坐标的偏差值
const int M = 250 * 250;
pair<int, int> z[M];//z[i]代表一个坐标
bool cmp(pair<int, int> a, pair<int, int> b){
return h[a.first][a.second] > h[b.first][b.second];
}
int main(){
n = read(), m = read();
int k = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
h[i][j] = read();//每个位置的高度
k++;
z[k] = make_pair(i, j);
}
}
sort(z + 1, z + k + 1, cmp);
for(int a = 1;a <= k;a++){
int i = z[a].first;
int j = z[a].second;
//取出当前坐标
//int h = ::h[i][j];
//取出当前坐标高度
f[i][j] = max(f[i][j], 1);
for(int d = 0;d < 4;d++){
int x = i + dx[d];
int y = j + dy[d];
//从 (i,j)沿着方向d走一格会走到(x, y)
if(x >= 1 && x <= n && y >= 1 && y <= m)//判断(x, y)是否合法
if(h[i][j] > h[x][y])//(i, j)高度比(x, y)高度更高
f[x][y] = max(f[x][y], f[i][j] + 1);
}
}
int ans = -1;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
ans = max(ans, f[i][j]);
cout << ans << endl;
return 0;
}
Problem 7
乌龟棋
- 长度为 \(N\) 的格子上有权值
- \(M\) 张牌,上面有 \(1-4\) 中的一个数
- 使用一张牌往前走几步
- 最大化经过的位置的权值和
思路:
f[i][j][k][l][r]
考虑优化
#include<bits/stdc++.h>
using namespace std;
int f[45][45][45][45];
int g[5];
int a[400];
int main()
{
int n,m;
cin>>n>>m;
int i,j,k,l;
for(i=1;i<=n;i++)
cin>>a[i];
f[0][0][0][0]=a[1];
for(i=1;i<=m;i++){
int x;
cin>>x;
g[x]++;
}
for(i=0;i<=g[1];i++)
for(j=0;j<=g[2];j++)
for(k=0;k<=g[3];k++)
for(l=0;l<=g[4];l++){
int move=1+i+2*j+3*k+4*l;
if(i!=0) f[i][j][k][l]=max(f[i][j][k][l],f[i-1][j][k][l]+a[move]);
if(j!=0) f[i][j][k][l]=max(f[i][j][k][l],f[i][j-1][k][l]+a[move]);
if(k!=0) f[i][j][k][l]=max(f[i][j][k][l],f[i][j][k-1][l]+a[move]);
if(l!=0) f[i][j][k][l]=max(f[i][j][k][l],f[i][j][k][l-1]+a[move]);
}
cout<<f[g[1]][g[2]][g[3]][g[4]]<<endl;
return 0;
}
区间dp
所有的操作都是针对区间进行,不会有跨越两个元素的情况
Problem 1
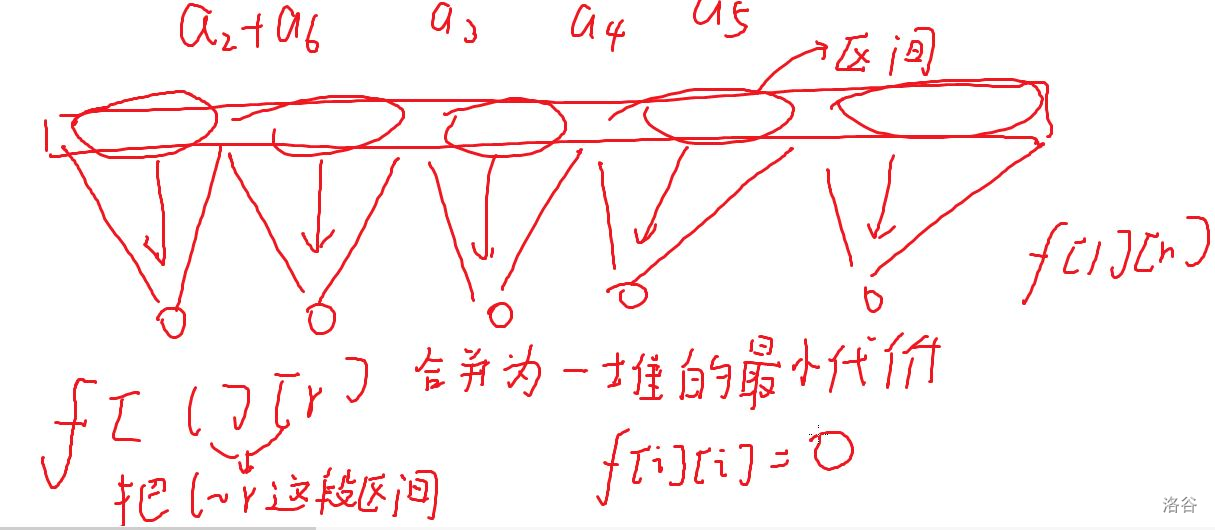
合并石子
- 每次选择相邻两堆
- 代价为两堆石子和
- 问最小总代价
思路:
用 \(𝑓[𝑚][𝑟]\) 表示一段区间合并的最小代价
枚举断点合并
如果是环形要如何处理?
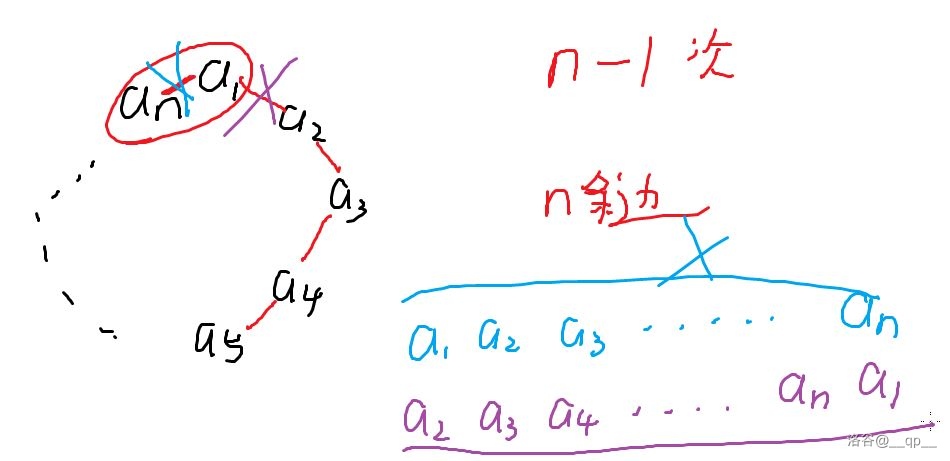
Problem 2
给出一个的只有 ()[] 四种括号组成的字符串,求最多能够选出多少个括号满足完全匹配
思路:
\(𝑓[𝑚][𝑟]\)代表该段区间能匹配的最多字符
- 转移一 枚举断点
- 转移二 去掉端点
- 转移三 匹配端点
Problem 3
给你 \(n\) 个数字
- 要求不能删除左右端点的数字
- 删除其他数字的代价是该数字和左右相邻数字的乘积
- 问把数字(除端点)删完后的最小总代价
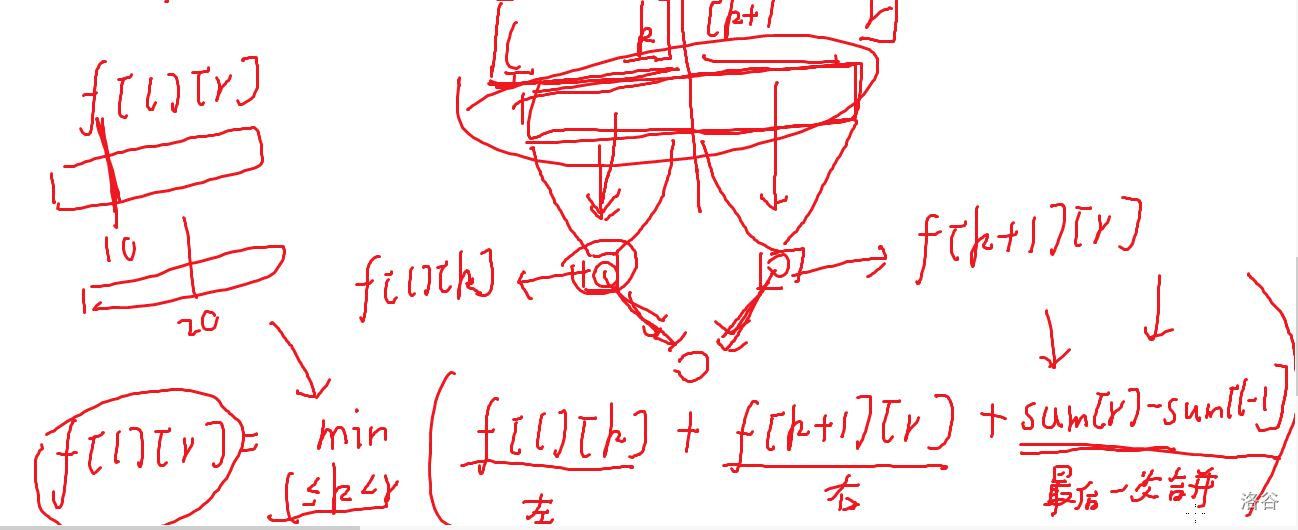
还是 \(𝑓[𝑚][𝑟]\)
注意:状态要表示为保留左右两张卡片
Problem 4
给定字符串,求回文子序列的数量
注:两个回文子序列只要位置不同就算做不同的回文子序列
思路:

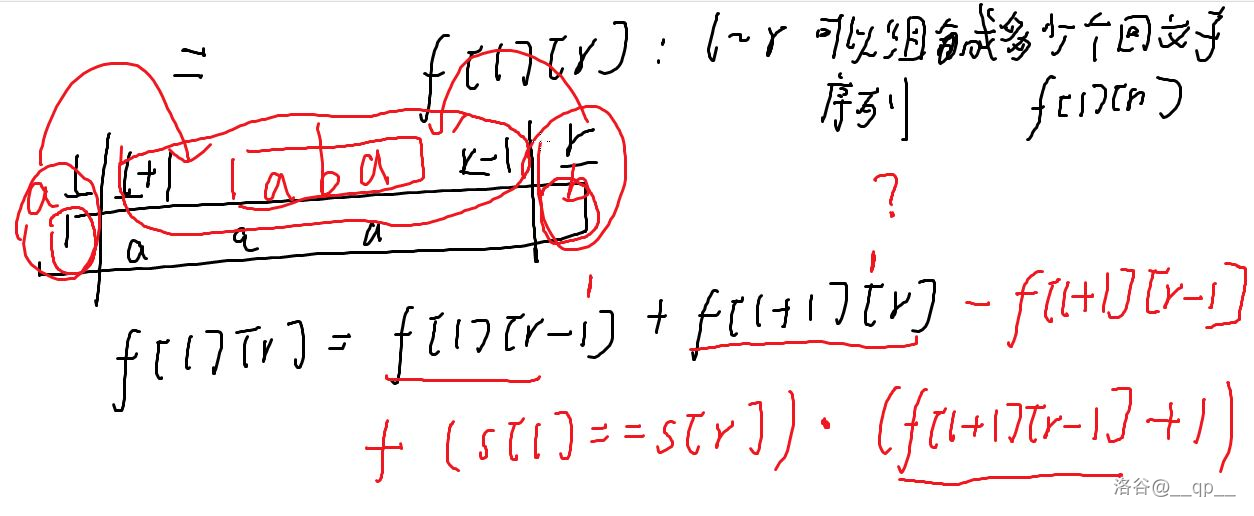
关键:去重
- 转移一:容斥原理
- 转移二:当左右字符相同时 再补充一次内部答案
Problem 5
给定凸 \(N\) 边形
- 每个点有一个权值
- 将凸多边形三角化
- 每个三角形的三个点权乘起来求和
- 问最小和
思路:
本质上是一个环形区间dp
背包
Problem 1
\(N\) 个物品 \(M\) 容量每个物品有体积和价值
- 最大化价值和
- 如果物品可以用无限次?
- 如果物品可以用有限次?
树形dp
本质:
基于树的dp
-
dp方法始终为从下至上进行dp
-
在每个节点对所有儿子做聚合
-
可能需要多一遍 dfs 或者 bfs
图的存储
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
const int MAXX = 1e5 + 10, MAXN = 1e9 + 10;
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n;
vector<int> z[MAXX];//z[i]代表从i出发的所有边 z[i][j]代表从i出发的第j条边会走到z[i]
int f[MAXX];
void dfs(int i, int fa){//当前dfs到了i点他的父亲是fa
//要求f[i]
for(auto j : z[i]){//从i->j的边
if(j != fa){
dfs(j, i);
}
}
f[i] = 1;
for(auto j : z[i]){//从i->j的边
if(j != fa){
f[i] += f[j];
}
}
}
int main(){
n = read();
for(int i = 1;i <= n;i++){
int s, e;
s = read(), e = read();
z[s].push_back(e);
z[e].push_back(s);
}
dfs(1, 0);
cout << f[1] << '\n';
return 0;
}
Problem 1
求树上有多少个点
思路:
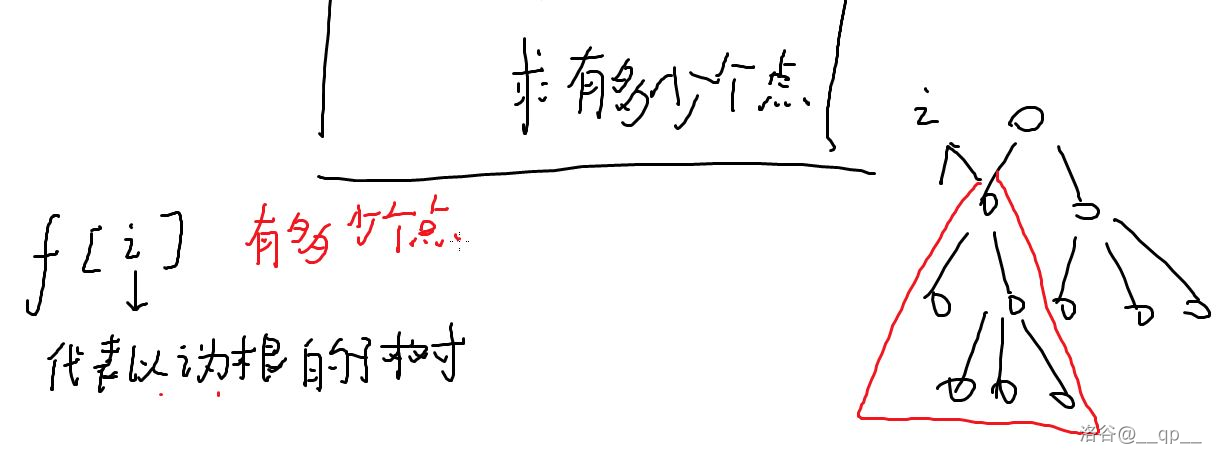

Problem 2
求树的直径
思路:
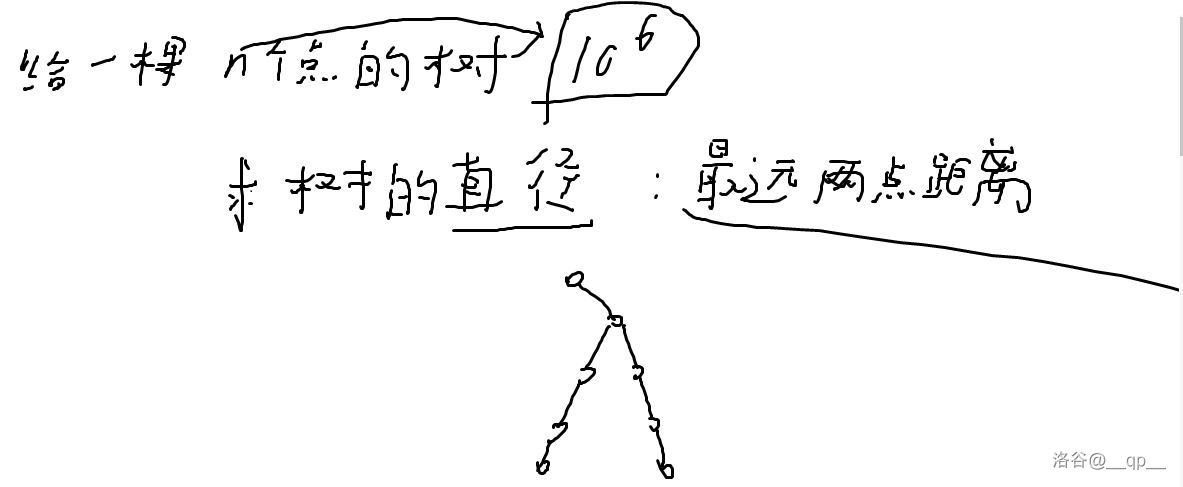
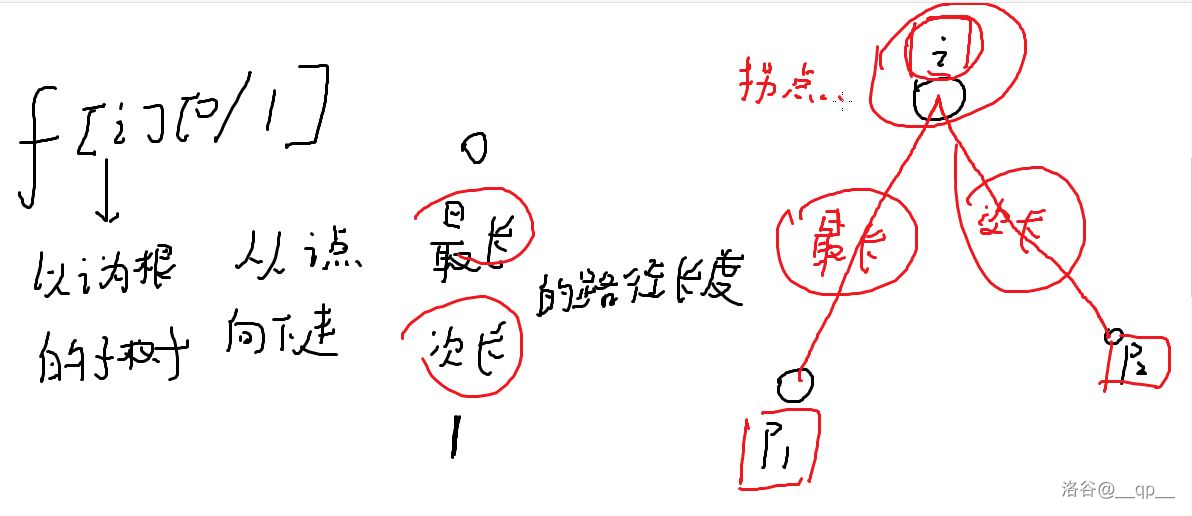
\(F[i][0]\) 最长
\(F[i][1]\) 次长
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
const int MAXX = 1e5 + 10, MAXN = 1e9 + 10;
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n;
int ans;
vector<int> z[MAXX];//z[i]代表从i出发的所有边 z[i][j]代表从i出发的第j条边会走到z[i]
int f[MAXX][2];//f[i][0/1]从i出发向下走最长或次长的路径长度
void dfs(int i, int fa){//当前dfs到了i点他的父亲是fa
//要求f[i]
for(auto j : z[i]){//从i->j的边
if(j != fa){
dfs(j, i);
}
}
priority_queue<int> heap;
heap.push(0);
heap.push(0);
for(auto j : z[i]){//从i->j的边
if(j != fa){
heap.push(f[j][0] + 1);
}
}
f[i][0] = heap.top();
heap.pop();
f[i][1] = heap.top();
ans = max(ans, f[i][0] + f[i][1]);
}
int main(){
n = read();
for(int i = 1;i <= n;i++){
int s, e;
s = read(), e = read();
z[s].push_back(e);
z[e].push_back(s);
}
dfs(1, 0);
cout << f[1] << '\n';
return 0;
}
Problem 3
求树上路径总长度和
思路:
F[i] 表示子树内答案
DP + Dfs
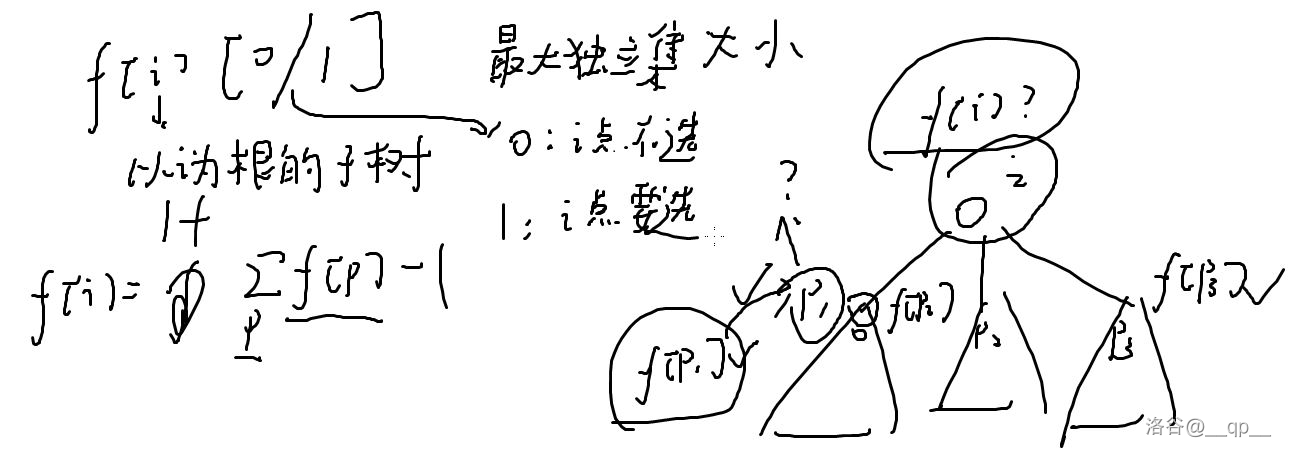
Problem 5
现在要在一棵树上布置士兵,每个士兵在结点上,每个士兵可以守护其结点直接相连的全部点,问最少需要布置多少个士兵。
Problem 6
一棵结点带权树,大小(结点数)为 \(k\) 的子树的权值和最大为多少。
数据范围 \(100\) 以内
Problem 7
依赖背包问题
每个物品要选必须先选某个指定的物品,问能够获得的最大价值




 浙公网安备 33010602011771号
浙公网安备 33010602011771号