软考4

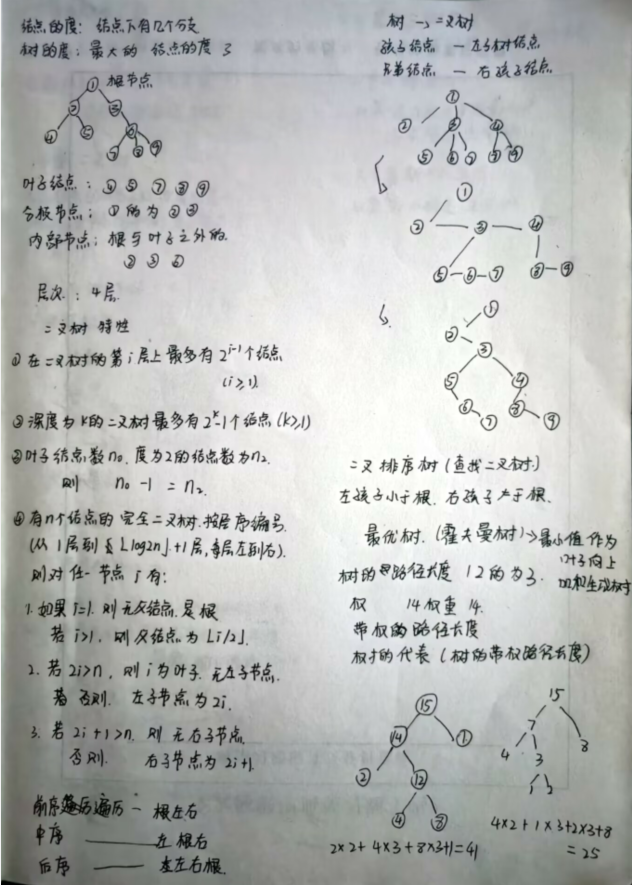
节点的度：节点下的分支数

树的度：最大的节点的度

 

二叉树的特性

　　在二叉树的第i层上最多有2^i-1个节点（i>=1）

　　深度为k的二叉树最多有2^k-1个节点（k>=1）

　　叶子节点数位n₀，度为2的节点数为n₂，则n₀ - 1 = n₂

　　有n个节点的完全二叉树，按层序编号（从第一层到第[log2n] + 1层，每层从左到右），则对任意节点i有

　　　　　　如果 i=1，则无父节点，是根；若 i>1，则父节点为[i/2]

　　　　　　如果2i>n，则i为叶子，无左节点；否则，左子节点为2i

　　　　　　如果2i+1>n，在无右节点；否则，右子节点为2i+1

 

前序遍历　　根左右

中序遍历　　左根右

后序遍历　　左右根

 

数转变为二叉树

　　　　孩子节点——左子树节点，兄弟节点——右孩子节点

 

二叉排序树（查找二叉树）

　　左孩子小于根，右孩子大于根

 

最优树（霍夫曼树）

　　最小值作为叶子，向上加和生成树

　树的带权路径长度最短

 

线索二叉树（前序线索二叉树、中序线索二叉树、后续线索二叉树）

　线索指前后节点

　空的指针指向前/后节点　　没有前/后节点时指向NULL

 

平衡二叉树

　　任意节点的左右子树深度相差不超过1，每节点的平衡度只能为-1、0、1

 

 

图的存储结构

　　　　邻接矩阵

　　　　邻接表

 

图的遍历

　　深度优先

　　广度优先

 

拓扑排序（结果不一定唯一）

用有向边表示活动之间开始的前后关系　　　　这种有向图称为用顶点表示活动网络，简称AOV网络

 

最小生成树　　　　不形成环路+访问所有节点

　　　　普利姆算法

　　　　　　　　以某一点为起点寻找最小权，逐步增加生成树

　　　　克鲁斯卡尔算法

　　　　　　　　权值最小相连生成树

 

笔记——