寒露将至，略有所感：过河卒 DP入门

 

 国庆假期已经接近尾声，我看了看这几天的代码，略有所得。

DP基础：

动态规划（Dynamic Programming，DP）是运筹学的一个分支，是求解决策过程最优化的过程。20世纪50年代初，美国数学家贝尔曼（R.Bellman）等人在研究多阶段决策过程的优化问题时，提出了著名的最优化原理，从而创立了动态规划。动态规划的应用极其广泛，包括工程技术、经济、工业生产、军事以及自动化控制等领域，并在背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等中取得了显著的效果。

---

例如洛谷的P1002（过河卒）一道较为入门的DP；

题目如下：

题目描述

棋盘上 A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，A点 (0, 0)B点 (n, m)同样马的位置坐标是需要给出的。

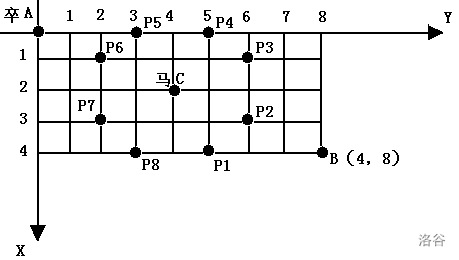
现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 BB 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

我们来模拟一下：A是A点 , B是B点, M是马的位置, X是马不能走的点。

 A 0 0 0 0 0 0
 0 0 X 0 X 0 0
 0 X 0 0 0 X 0
 0 0 0 M 0 0 0
 0 X 0 0 0 X 0
 0 0 X 0 X 0 0
 0 0 0 0 0 0 B
所以便有转移方程：

f[i][j]=max(f[i−1][j]+f[i][j−1],f[i][j])

#include<iostream>
using namespace std;
int dir[8][2]={{1,2},{1,-2},{2,1},{2,-1},{-1,2},{-2,1},{-1,-2},{-2,-1}}; 
bool d[30][30];
long long dp[30][30];
int main(){
	int n,m,cx,cy;
	//n,m棋盘大小 cx cy马的位置 
	cin>>n>>m>>cx>>cy;
	d[cx][cy]=true;
	for(int i=0;i<8;i++){
		int tx=cx+dir[i][0];
		int ty=cy+dir[i][1];
		if(tx>=0&&tx<=n&&ty>=0&&ty<=m){
			d[tx][ty]=true;
		}
	}
	dp[0][0]=1;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=m;j++){
			if(d[i][j]==false){
				if(i){
					dp[i][j]+=dp[i-1][j];
				}
				if(j){
					dp[i][j]+=dp[i][j-1];
				}
			}
		}
	}
	cout<<dp[n][m]<<endl;
}