堆排序

堆

  （二叉）堆是一个数组，可被看成一个近似的完全二叉树，树上的每一个结点对应数组中的一个元素，除了最底层外，该树是完全充满的，而且是从左向右填充。

     树的根结点为A[1]，给定一个结点的下标i，则父结点、左孩子、右孩子结点下标为：

     Parent(i)

       return i/2

     Left(i)

       return 2i

     Right(i)

       return 2i+1

 

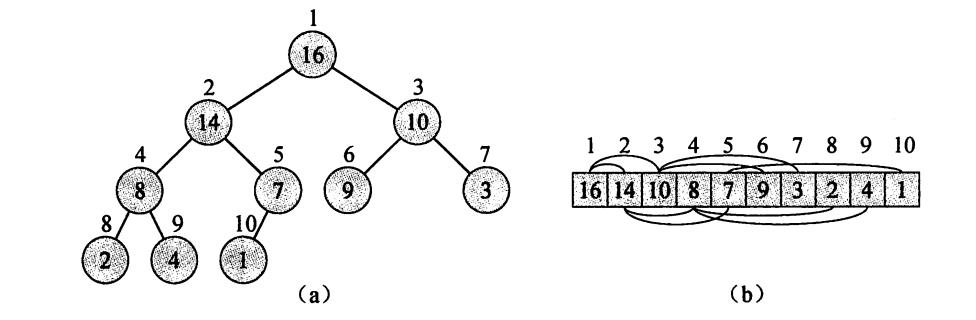
二叉堆分为最大堆和最小堆，最大堆的性质为除了根以外的所有结点i都要满足A[Parent(i)]≥A[i]，最小堆则相反，即A[Parent(i)]≤A[i]。最小堆通常用于构造优先队列。

维护堆的性质

      maxHeapify为维护最大堆的重要过程，输入为数组A和下标i，假定根节点为Left(i)和Ringht(i)的二叉树都是最大堆，结点A[i]可能小于其孩子，违背了最大堆的性质，maxHeapify通过让A[i]的值在最大堆中“逐级下降”从而使得以下标i为结点的子树重新遵循最大堆性质。

 

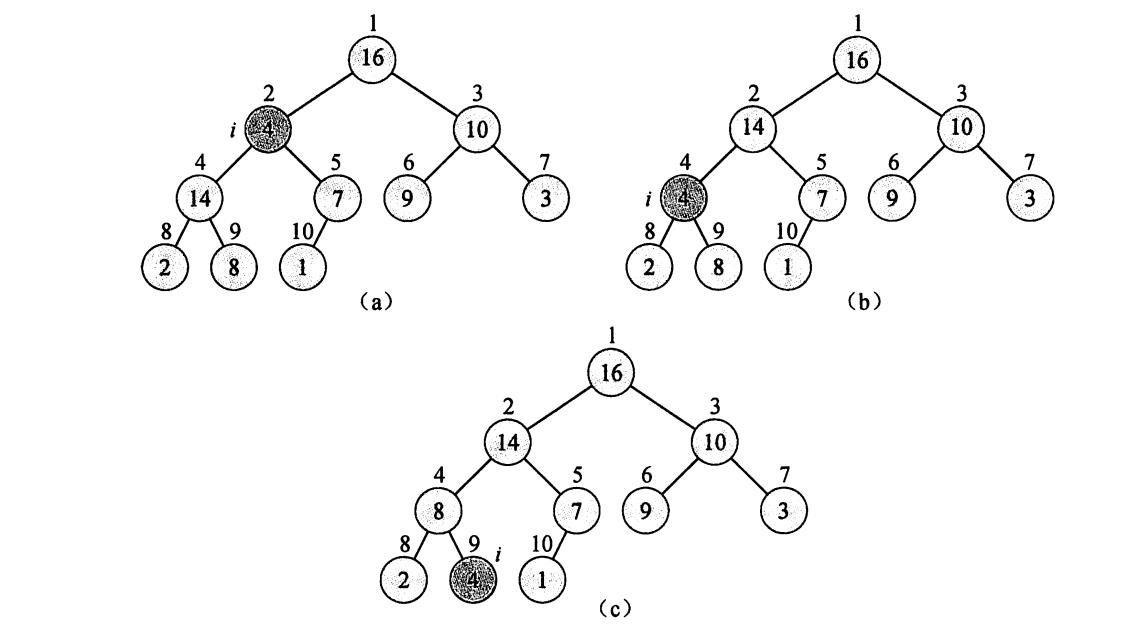
void maxHeapify(int A[],int i)
{
    int l=2*i;
    int r=2*i+1;
    int largest=i;
    if(l<=heapsize&&A[l]>A[i])
        largest=l;
    if(r<=heapsize&&A[r]>A[largest])
        largest=r;
    if(largest!=i)
    {
        int tmp=A[i];
        A[i]=A[largest];
        A[largest]=tmp;
        maxHeapify(A,largest);
    }
}

 

 

 

建堆

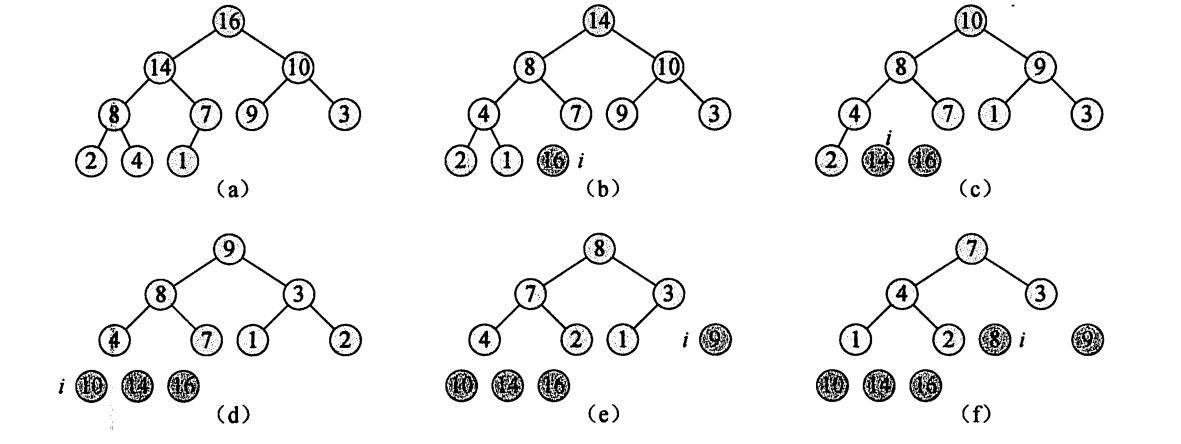
      用自底向上的方法利用过程maxHeapify把一个大小为n=A.length的数组转化为最大堆。

      子数组A([n/2]+1...n)中的元素都是树的叶结点。每个叶结点都可以看成只包含一个元素的堆，过程buildMaxHeap对树中的其它结点都调用一次maxHeapify

void buildMaxHeap(int A[])
{
    heapsize=length;
    for(int i=length/2; i>=1; i--)
        maxHeapify(A,i);
}

 

堆排序算法

      初始时，堆排序算法利用buildMaxHeap将输入数组建成最大堆，因为数组中的最大堆元素总在根结点A[1]中，通过把它与A[n]进行互换，可以把该元素放到正确的位置。此时，从堆中去掉结点n，剩余结点中，原来根的孩子结点仍是最大堆，而新的根结点可能会违背最大堆的性质，可以调用maxHeapify(A,1)从而在A[1...n-1]上构造一个新的最大堆。堆排序算法会不断重复这一过程。直到堆的大小从n-1降到2。

void heapSort(int A[])
{
    buildMaxHeap(A);
    for(int i=length; i>=2; i--)
    {
        int tmp=A[1];
        A[1]=A[i];
        A[i]=tmp;
        heapsize--;
        maxHeapify(A,1);
    }
}

完整代码

#include<iostream>
using namespace std;
int heapsize,length;
void maxHeapify(int A[],int i)
{
    int l=2*i;
    int r=2*i+1;
    int largest=i;
    if(l<=heapsize&&A[l]>A[i])
        largest=l;
    if(r<=heapsize&&A[r]>A[largest])
        largest=r;
    if(largest!=i)
    {
        int tmp=A[i];
        A[i]=A[largest];
        A[largest]=tmp;
        maxHeapify(A,largest);
    }
}
void buildMaxHeap(int A[])
{
    heapsize=length;
    for(int i=length/2; i>=1; i--)
        maxHeapify(A,i);
}
void heapSort(int A[])
{
    buildMaxHeap(A);
    for(int i=length; i>=2; i--)
    {
        int tmp=A[1];
        A[1]=A[i];
        A[i]=tmp;
        heapsize--;
        maxHeapify(A,1);
    }
}
int main()
{
    int A[20];
    cin>>length;
    for(int i=1; i<=length; i++)
        cin>>A[i];
    heapSort(A);
    for(int i=1; i<=length; i++)
        cout<<A[i]<<" ";
    cout<<endl;
    return 0;
}