【算法通关指南:基础算法篇】高精度专题:一篇破除超数运算挑战

小龙报:个人主页
作者简介:C++研发,嵌入式,机器人方向学习者
❄️个人专栏:《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录
前言
本专栏聚焦算法题实战,系统讲解算法模块:以《c++编程》,《数据结构和算法》《基础算法》《算法实战》 等几个板块以题带点,讲解思路与代码实现,帮助大家快速提升代码能力
ps:本章节题目分两部分,比较基础笔者只附上代码供大家参考,其他的笔者会附上自己的思考和讲解,希望和大家一起努力见证自己的算法成长
一、高精度
当数据的值特别大,各种类型都存不下的时候,此时就要用高精度算法来计算加减乘除高精度算法本质上还是模拟算法,用代码模拟小学列竖式计算加减乘除的过程
二、高精度加法
2.1【模板】加法
2.1.1题目
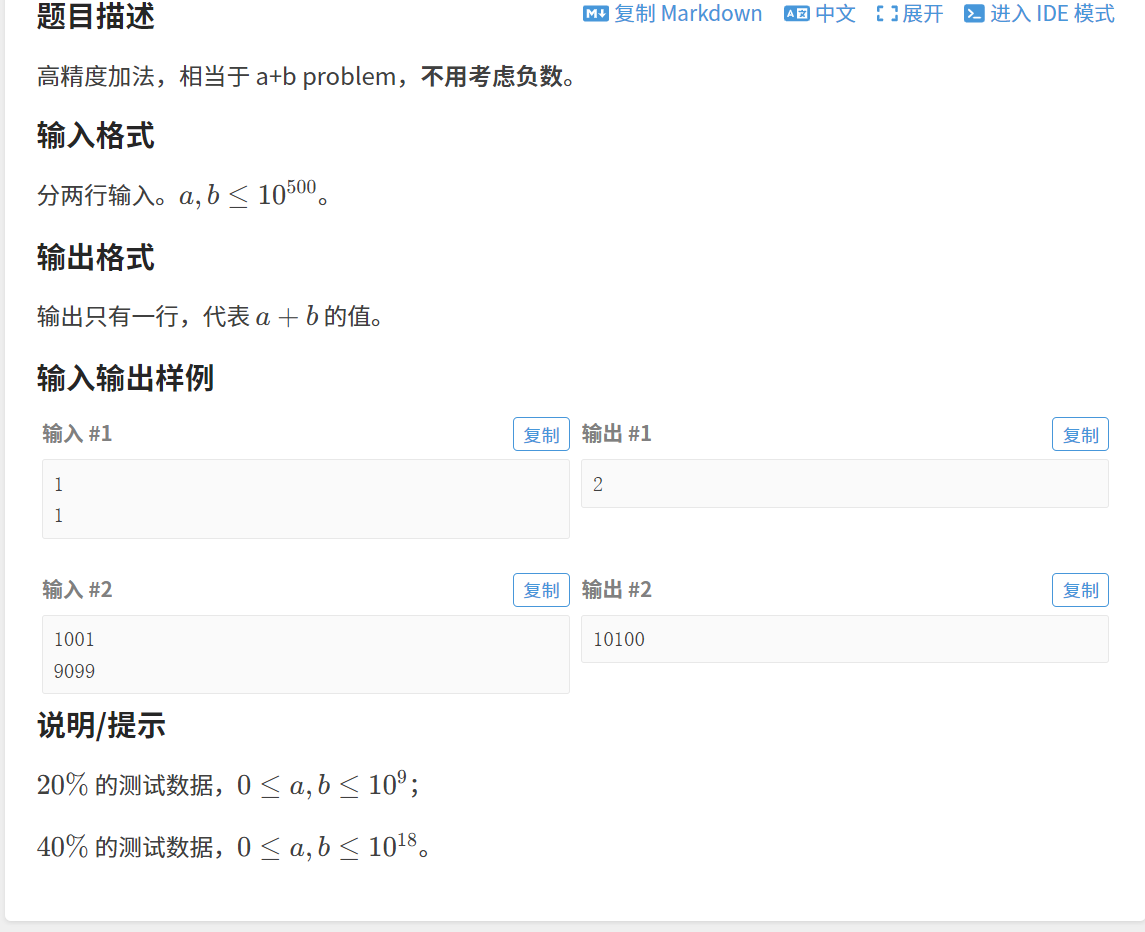
2.1.2 算法原理
模拟小学「列竖式」计算「两数相加」的过程
核心步骤 :
(1)先用字符串读入这个数,然后用数组逆序存储该数的每⼀位;
(2)利用数组,模拟加减乘除运算的过程
2.2.3代码
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
int la, lb, lc;
void add(int a[], int b[], int c[])
{
for (int i = 0; i < lc; i++)
{
c[i] += a[i] + b[i]; // 对应位相加,再加上进位
c[i + 1] += c[i] / 10; // 处理进位
c[i] %= 10; //处理余数
if (c[lc])
lc++;
}
}
int main()
{
string x, y;
cin >> x >> y;
la = x.size();
lb = y.size();
lc = max(la, lb);
for (int i = 0; i < la; i++)
a[la - i - 1] = x[i] - '0';
for (int i = 0; i < lb; i++)
b[lb - i - 1] = y[i] - '0';
add(a, b, c);
for (int i = lc - 1; i >= 0; i--)
cout << c[i];
return 0;
}三、高精度减法
3.1【模板】减法
3.1.1题目
链接:高精度减法
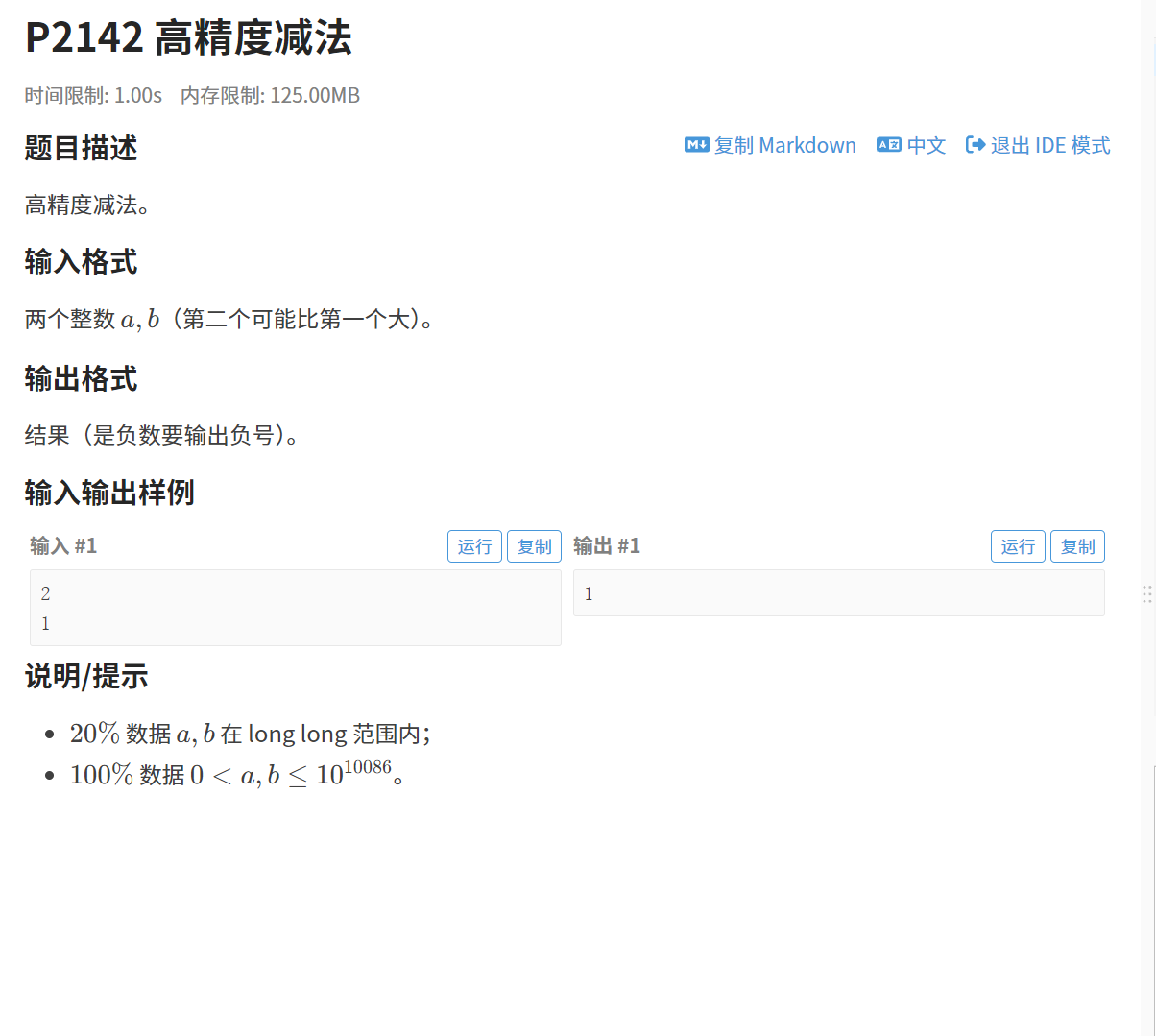
3.1.2 算法原理
模拟小学「列竖式」计算「两数相减」的过程
核心步骤 :
(1)用字符串读入数据;
(2)判断两个数的大小,让较大的数在前。注意字典序vs数的大小:
a. 位数相等:按字典序比较;
b. 位数不等:按照字符串的长度比较。
(3)将字符串的每⼀位拆分,逆序放在数组中;
(4)模拟列竖式计算的过程:
a. 对应位求差;
b. 处理借位;
(5) 处理前导零。
3.2.3代码
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];
string x, y;
int la,lb,lc;
bool cmp(string& x, string& y)
{
//先比较长度
if (x.size() != y.size())
return x.size() < y.size();
//按字典序比较
return x < y;
}
void sub(int c[], int a[], int b[])
{
for (int i = 0; i < lc; i++)
{
c[i] += a[i] - b[i];
if (c[i] < 0)
{
c[i + 1] -= 1; //向高位借位
c[i] += 10;
}
}
while (lc > 1 && c[lc - 1] == 0)
lc--;
}
int main()
{
cin >> x >> y;
//处理负数问题
if (cmp(x, y))
{
swap(x, y);
cout << '-';
}
la = x.size();
lb = y.size();
lc = max(la, lb);
for (int i = 0; i < la; i++)
a[la - i - 1] = x[i] - '0';
for (int i = 0; i < lb; i++)
b[lb - i - 1] = y[i] - '0';
sub(c, a, b); // c = a - b
for (int i = lc - 1; i >= 0; i--)
cout << c[i];
return 0;
}四、高精度乘法
4.1【模板】乘法
4.1.1题目
链接:A*B Problem
4.1.2 算法原理
无进位相乘再相加:
• 还是「列竖式」,但是每⼀位相乘的时候不考虑进位,直接把乘的结果放在对应位上;
• 等到所有对应位置「乘完」并且「累加完」之后,「统⼀处理进位」
核心步骤 :
(1)用字符串读⼊数据;
(2)将字符串的每⼀位拆分,逆序放在数组中;
(3)模拟无进位相乘再相加的过程:
a. 对应位求乘积;
b. 乘完之后处理进位;
c. 处理余数;
4. 处理前导零。
4.2.3代码
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], b[N], c[N];
string x, y;
int la, lb, lc;
void mul(int c[], int a[], int b[])
{
// ⽆进位相乘,然后相加
for (int i = 0; i < la; i++)
{
for (int j = 0; j < lb; j++)
c[i + j] += a[i] * b[j];
}
//处理进位
for (int i = 0; i < lc; i++)
{
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
// 处理前导零
while (lc > 1 && c[lc - 1] == 0)
lc--;
}
int main()
{
cin >> x >> y;
la = x.size();
lb = y.size();
lc = la + lb;
for (int i = 0; i < la; i++)
a[la - i - 1] = x[i] - '0';
for (int i = 0; i < lb; i++)
b[lb - i - 1] = y[i] - '0';
mul(c, a, b); //c = a * b;
for (int i = lc - 1; i >= 0; i--)
cout << c[i];
return 0;
}五、高精度除法
5.1【模板】除法
5.1.1题目
链接:A/B Problem
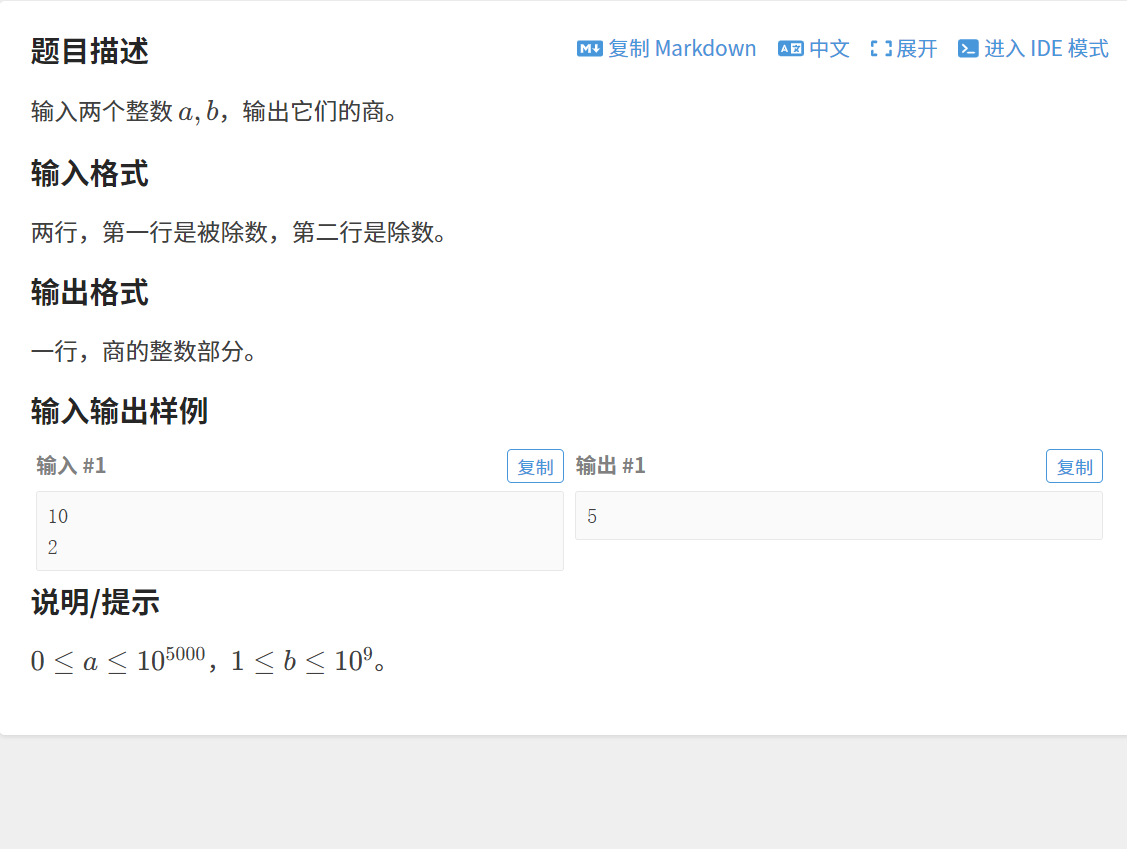
5.1.2 算法原理
模拟小学「列竖式」计算「两数相除」的过程(注意,我们这里是「高精度 ÷ 低精度」)。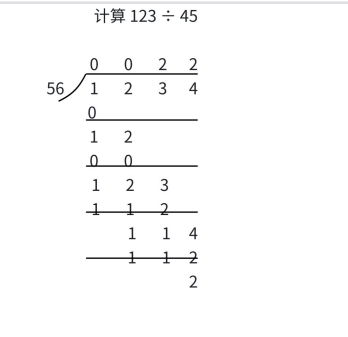
核心步骤 :
定义⼀个指针i 从「高位」遍历被除数,⼀个变量t 标记当前「被除的数」,记除数是b ;
• 更新⼀个当前被除的数t = t × 10 + a[i] ;
• t/b 表⽰这⼀位的商,t%b 这⼀位的余数;
• ⽤t 记录这⼀次的余数,遍历到下⼀位的时候重复上⾯的过程
被除数遍历完毕之后,t ⾥⾯存的就是余数,但是商可能存在前导0 ,注意清空
5.2.3代码
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
int a[N], b, c[N];
string x;
int la;
void sub(int c[], int a[], int b)
{
LL t = 0;
for (int i = la - 1; i >= 0; i--)
{
//当前被除数
t = t * 10 + a[i];
c[i] = t / b;
t %= b;
}
//处理前导零
while (la > 1 && c[la - 1] == 0)
la--;
}
int main()
{
cin >> x >> b;
la = x.size();
for (int i = 0; i < la; i++)
a[la - i - 1] = x[i] - '0';
sub(c, a, b); //c = a / b;
for (int i = la - 1; i >= 0; i--)
cout << c[i];
return 0;
}总结与每日励志
✨ 本文介绍了高精度算法的原理和实现,包括高精度加法、减法、乘法和除法的模板代码。高精度算法通过字符串读入大数,逆序存储在数组中,模拟小学列竖式计算过程,解决常规数据类型无法存储超大数值的问题。加法、减法和乘法部分详细讲解了算法步骤和代码实现,除法部分则针对高精度除以低精度的情况进行说明。所有算法都包含处理进位、借位和前导零的关键步骤,并附有完整代码示例,帮助读者掌握高精度计算的实现方法。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号