详细介绍：进阶数据结构应用-单词

目录

• • 题目-单词
  • 问题分析
  • 算法步骤
  • 代码实现

题目-单词

问题分析

目标是每个单词出现的次数, 分为两类

• 如果当前单词不是某个单词子串, 那么出现次数是$1$
• 如果当前单词是某个单词的子串, 如何计算次数?

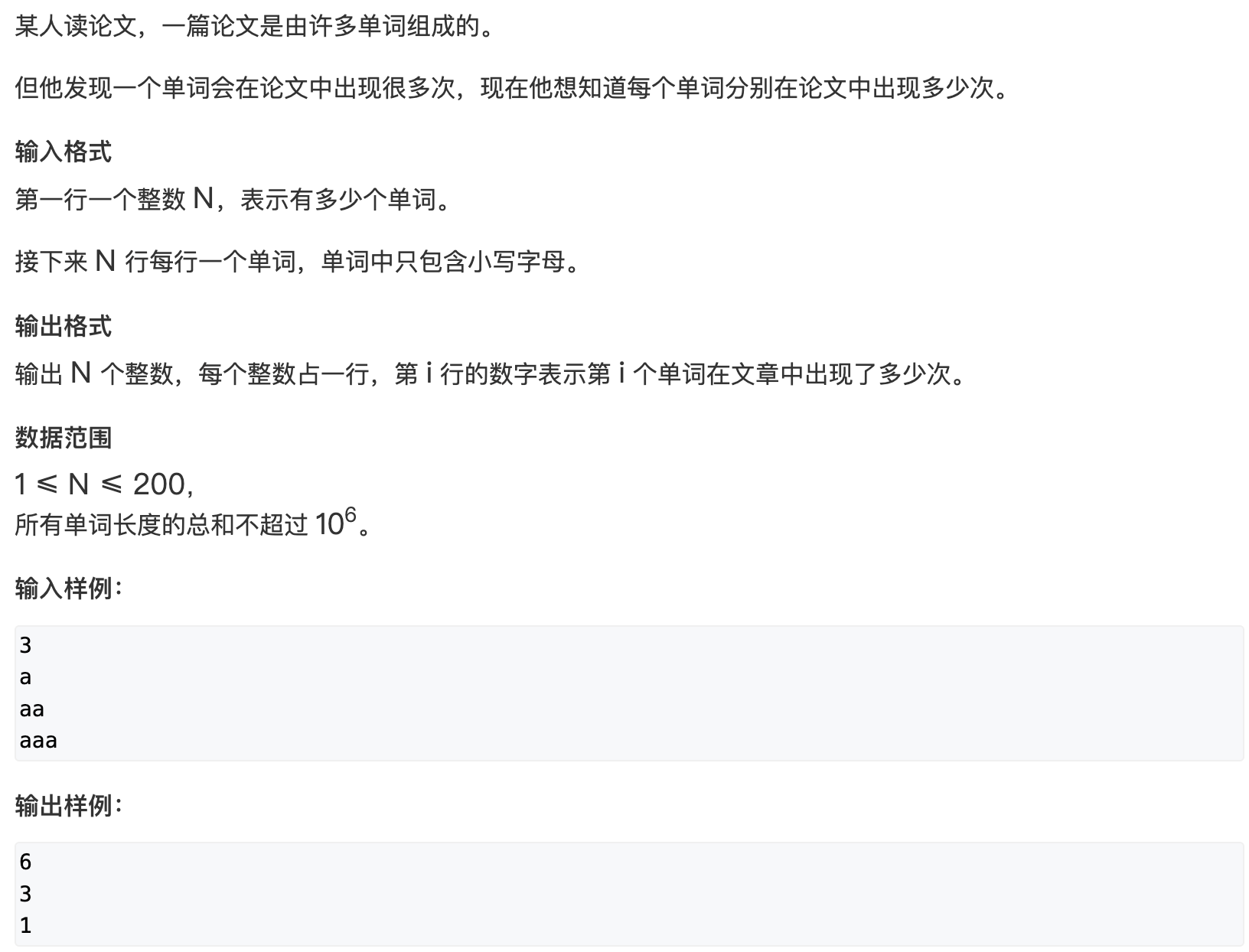
我们可以统计这样一个数值, 对于串$s$, 以就是有多少个前缀$s$为后缀的, 这个值就是答案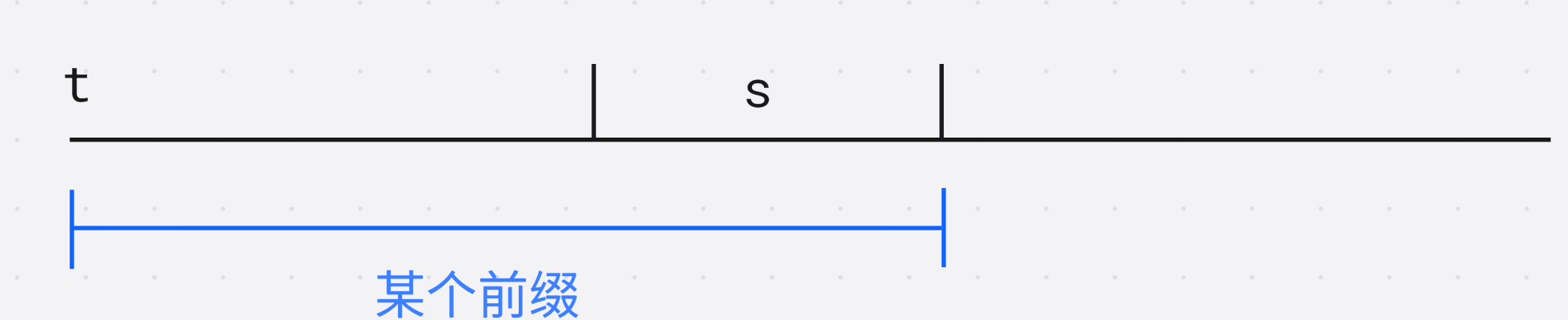

对于字符串$t$, 某一个前缀的后缀是$s$, 那么答案需要累计

如何计算?
对于当前串$s$, 计算当前后缀和哪些前缀匹配, 在AC自动机直接能够迭代计算

fail[u], fail[fail[u]], fail[fail[fail[u]]]…都是和当前后缀匹配的前缀

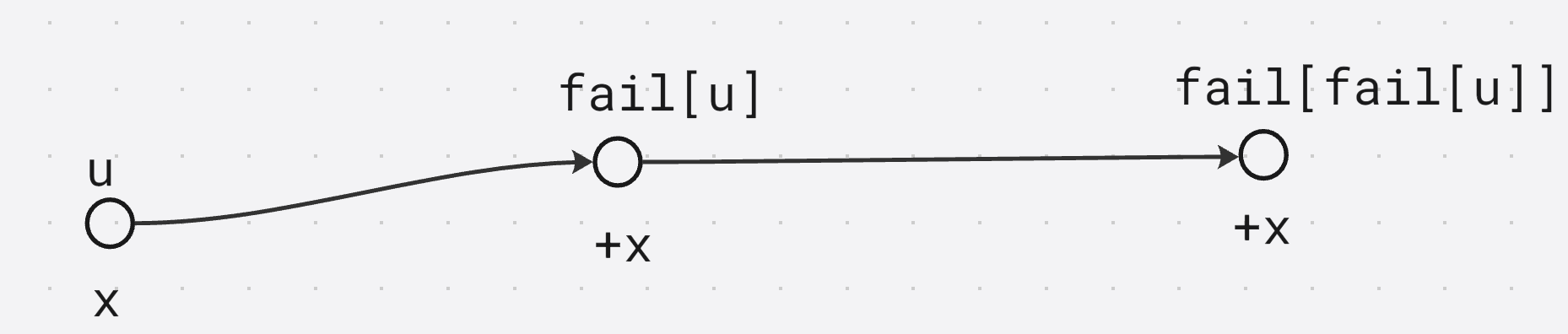
递推思想, 对于当前后缀出现次数假设是$x$, 将前面的前缀全部累加$+x$
例如某个后缀是aaa, 与之匹配的aa前缀也需要$+1$, 与aa匹配的前缀a也需要$+1$

因此直接按照AC自动机的fail指针拓扑序逆序递推就能得到答案

算法步骤

• 将读入的字符串加入到Trie中, 假设当前遍历的是节点$u$, $u$作为后缀出现次数累加cnt[u]++
• 假设当前添加的是第$k$个字符串, 当字符串添加完毕后, 记录结尾的Trie指针id[k] = u
• 构建AC自动机
• 按照拓扑序逆序从后向前递推, 因为后面的是更长的后缀, cnt[fail[i]] += cnt[i]
• 按照$id$计算每个字符串出现的次数

代码实现

#include <bits/stdc++.h>
  using namespace std;
  const int N = 210, M = 1e6 + 10;
  int n;
  int tr[M][26], idx;
  int f[M];
  int q[M], h, t;
  int fail[M], id[N];
  void insert(string &s, int k) {
  int p = 0;
  for (int i = 0; s[i]; ++i) {
  int c = s[i] - 'a';
  if (!tr[p][c]) tr[p][c] = ++idx;
  p = tr[p][c];
  // 因为p是代表某个后缀, 因此需要在p = tr[p][c]后面f[p]++
  f[p]++;
  }
  id[k] = p;
  }
  void build() {
  h = 0, t = -1;
  for (int i = 0; i < 26; ++i) {
  if (tr[0][i]) q[++t] = tr[0][i];
  }
  while (h <= t) {
  int u = q[h++];
  for (int i = 0; i < 26; ++i) {
  int v = tr[u][i];
  if (!v) continue;
  int j = fail[u];
  while (j && !tr[j][i]) j = fail[j];
  if (tr[j][i]) j = tr[j][i];
  fail[v] = j;
  q[++t] = v;
  }
  }
  }
  int main() {
  ios::sync_with_stdio(false);
  cin.tie(0);
  cin >> n;
  string s;
  for (int i = 0; i < n; ++i) {
  cin >> s;
  insert(s, i);
  }
  build();
  for (int i = t; i >= 0; --i) {
  int u = q[i];
  f[fail[u]] += f[u];
  }
  for (int i = 0; i < n; ++i) cout << f[id[i]] << '\n';
  return 0;
  }