深入解析:蓝桥杯基础算法精讲:模拟与高精度运算实战指南


前言
大家好啊,我是云泽Q,欢迎阅读我的文章,一名热爱计算机技术的在校大学生,喜欢在课余时间做一些计算机技术的总结性文章,希望我的文章能为你解答困惑~
一、模拟
1.1 多项式输出
多项式输出
解法
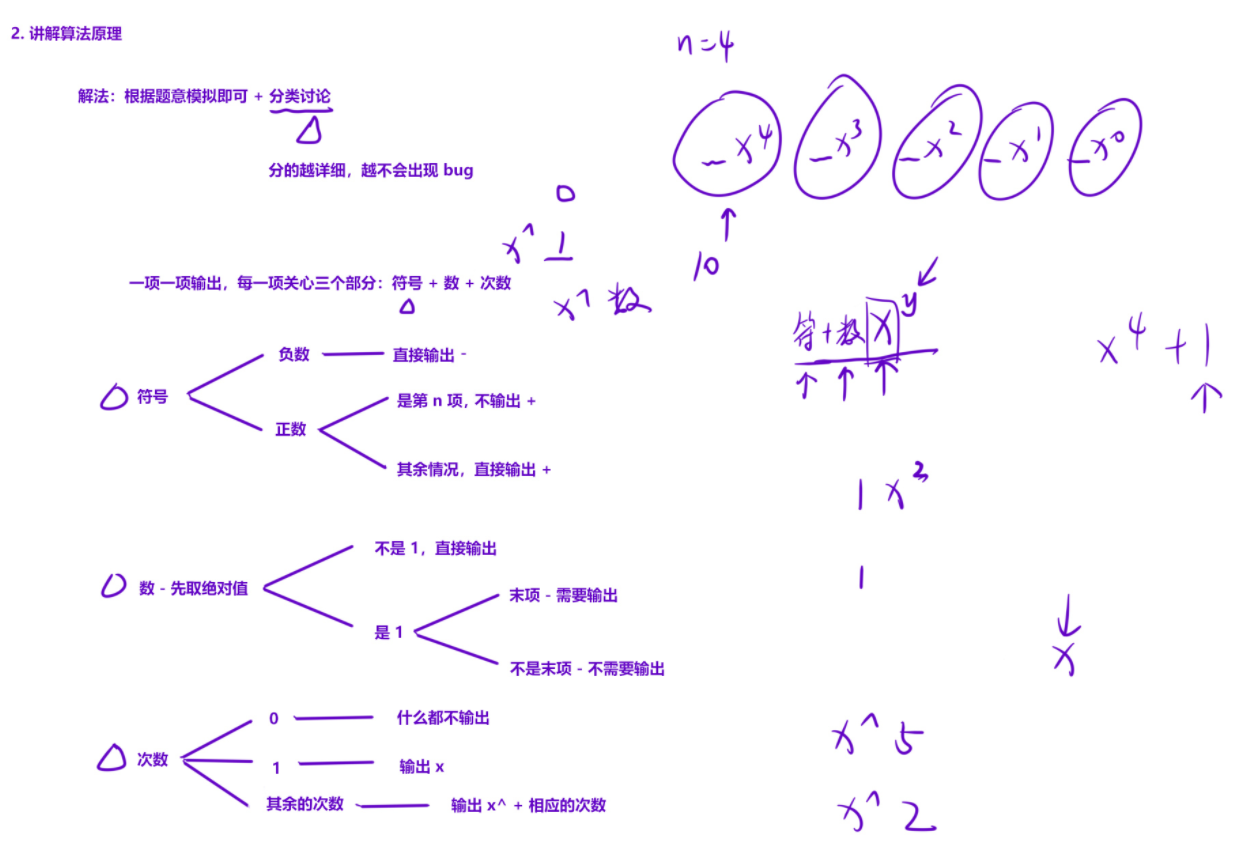
模拟 + 分类讨论,对于一元 n 次方程的最终结果,我们仅需按照顺序,考虑每一项的三件事情:符号 + 系数 + 次数
- 处理符号
- 如果系数小于0,直接输出“ - ”;
- 如果系数大于0,除了首项不输出“ + ”,其余全部输出“ + ”
- 处理系数
- 先取绝对值,因为正负问题已经处理过了
- 当系数不为1,直接输出这个数
- 但当系数为1,且是最后一项的时候,这个 1 也需要输出;其余情况下 1 不需要输出
- 处理次数
- 次数大于1,输出“ x^ ” + 对应的次数
- 次数等于1,输出“ x ”;
- 次数小于1,什么也不输出

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
int n; cin >> n;
for(int i = n; i >= 0; i--)
{
//前置0
int a; cin >> a;
if(a == 0) continue;
//符号
if(a < 0) cout << '-';
else{
if(i != n) cout << '+';
}
//系数
a = abs(a);
if(a != 1 || (a == 1 && i == 0)) cout << a;
//次数
if(i == 0) continue;
else if(i == 1) cout << 'x';
else cout << "x^" << i;
}
return 0;
}补充一下代码中continue的作用分析
这段代码用于处理多项式的输出:
第一处:if(a == 0) continue;(第 12 行)
作用:当当前项的系数a为 0 时,跳过对该次项的所有处理,直接进入下一次循环。
原因:根据题目要求 “多项式中只包含系数不为 0 的项”,系数为 0 的项无需输出,因此用continue跳过后续的符号、系数、次数等处理步骤。
第二处:if(i == 0) continue;(第 22 行)
作用:当当前项的次数i为 0 时,跳过后续关于x的次数相关输出(如x或x^i)。
原因:次数为 0 的项是常数项(形式为a,不含x),在前面已经处理完系数的输出后,不需要再输出x相关的内容,因此用continue跳过第 23-24 行对x的处理代码。
再补充说一下,这里代码的逻辑明明是一项一项的系数输入进行处理的,在实际输入的时候却可以一次性把所有的系数输入进去的原因
核心原因是C++ 的输入流(cin)会自动处理输入缓冲区中的空白字符(空格、回车、制表符等),具体逻辑如下:
- 代码的输入逻辑:代码中通过for循环从i = n遍历到i = 0(共n+1次循环),每次循环内都有cin >> a;,表示每次循环需要读取一个整数a(即一个系数)。
- cin的工作方式:当使用cin >> a读取整数时,cin会做两件关键事情:
- 自动跳过所有空白字符(空格、回车、制表符等),直到找到第一个非空白字符;
- 从该非空白字符开始读取,直到遇到下一个空白字符或输入结束,将读取到的内容转换为整数并赋值给a。
- 一次性输入的原理:
当 “一次性输入所有系数”(比如输入3 2 -1 5,用空格分隔),这些数据会被先存入输入缓冲区。
循环第一次执行时,cin >> a从缓冲区读取第一个数;
循环第二次执行时,cin >> a会跳过中间的空白字符,读取第二个数;
以此类推,直到读完n+1个系数,完全匹配循环次数。
举例说明
假设n = 2(即需要输入 3 个系数,对应x²、x¹、x⁰项):
- 你可以分 3 次输入:先输入2回车,再输入-1回车,最后输入3回车;
- 也可以一次性输入:2 -1 3然后回车。
这两种方式对程序来说效果完全相同,因为cin会自动忽略空格和回车,按顺序从缓冲区中读取 3 个整数,分别在 3 次循环中赋值给a。
1.2 蛇形方阵
蛇形方阵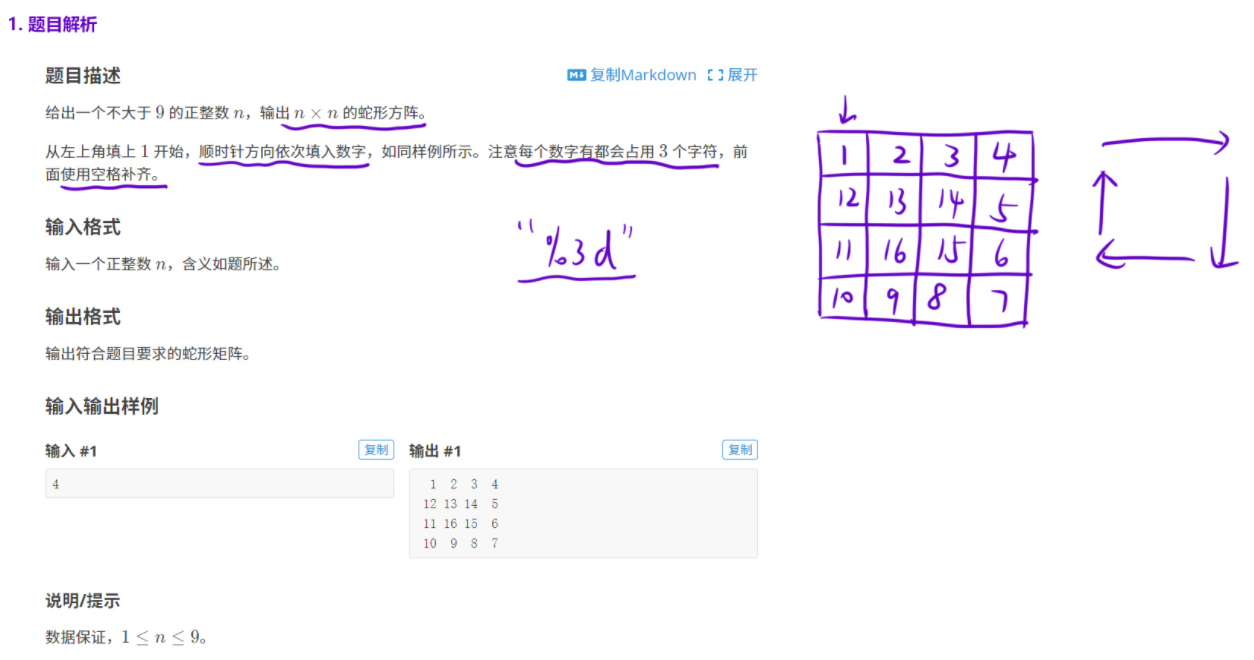
解法
模拟填数的过程
在一个矩阵中按照一定规律填数的通用解法:
- 定义方向向量,比如本题一共四个方向,分别是右、下、左、上,对应:
(0,1)、(1、0)、(0,-1)、(-1,0) - 循环填数的规则:
- 朝一个方向走,一边走一边填数,直到越界
- 越界之后,结合定义的方向向量,求出下一轮应该走的方向以及应该到达的正确位置;
- 重复上述过程,直到把所有的数填完为止
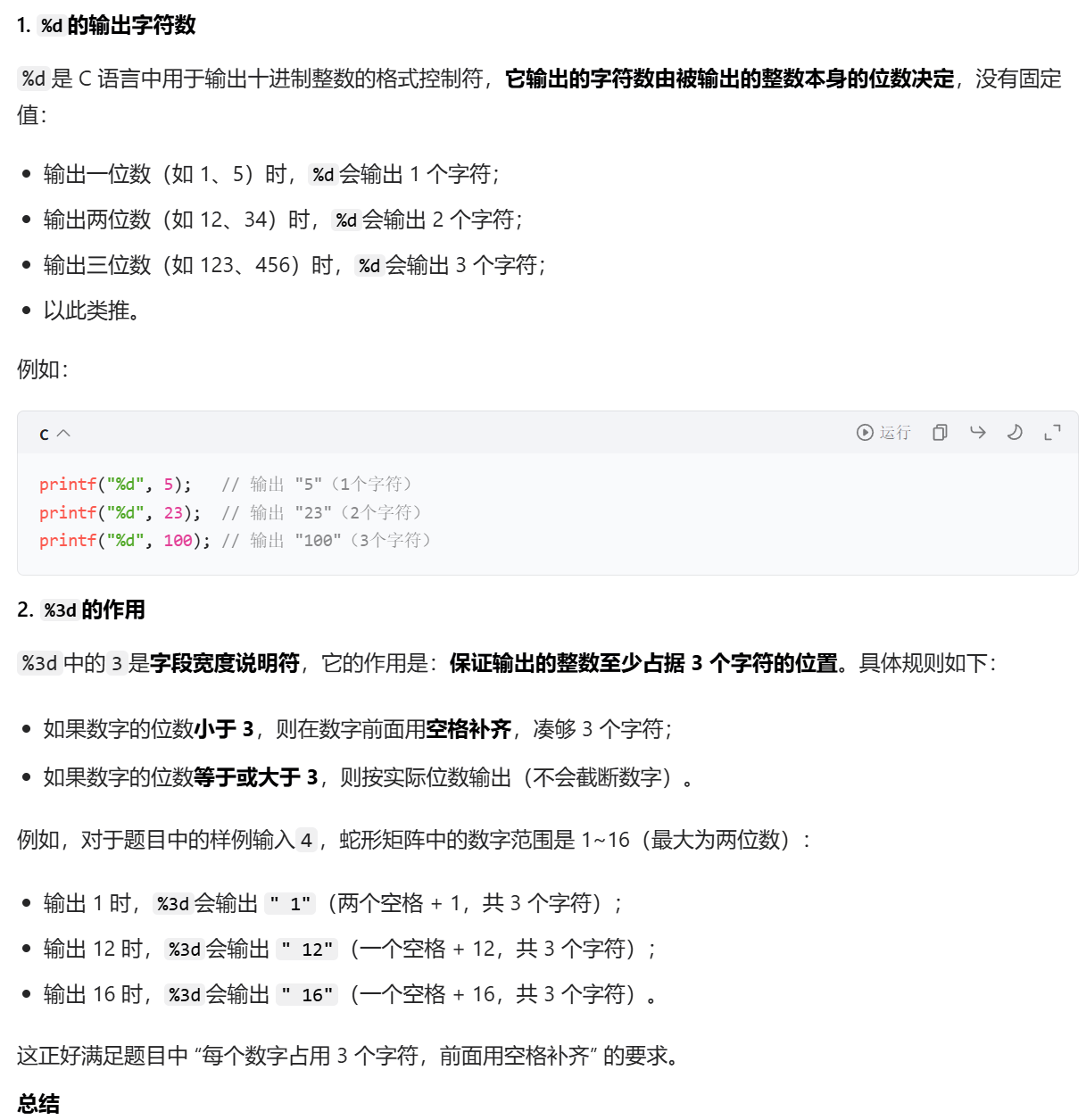
因为题目中说每个数字都会占用3个字符,所以输出的格式是以%3d的格式输出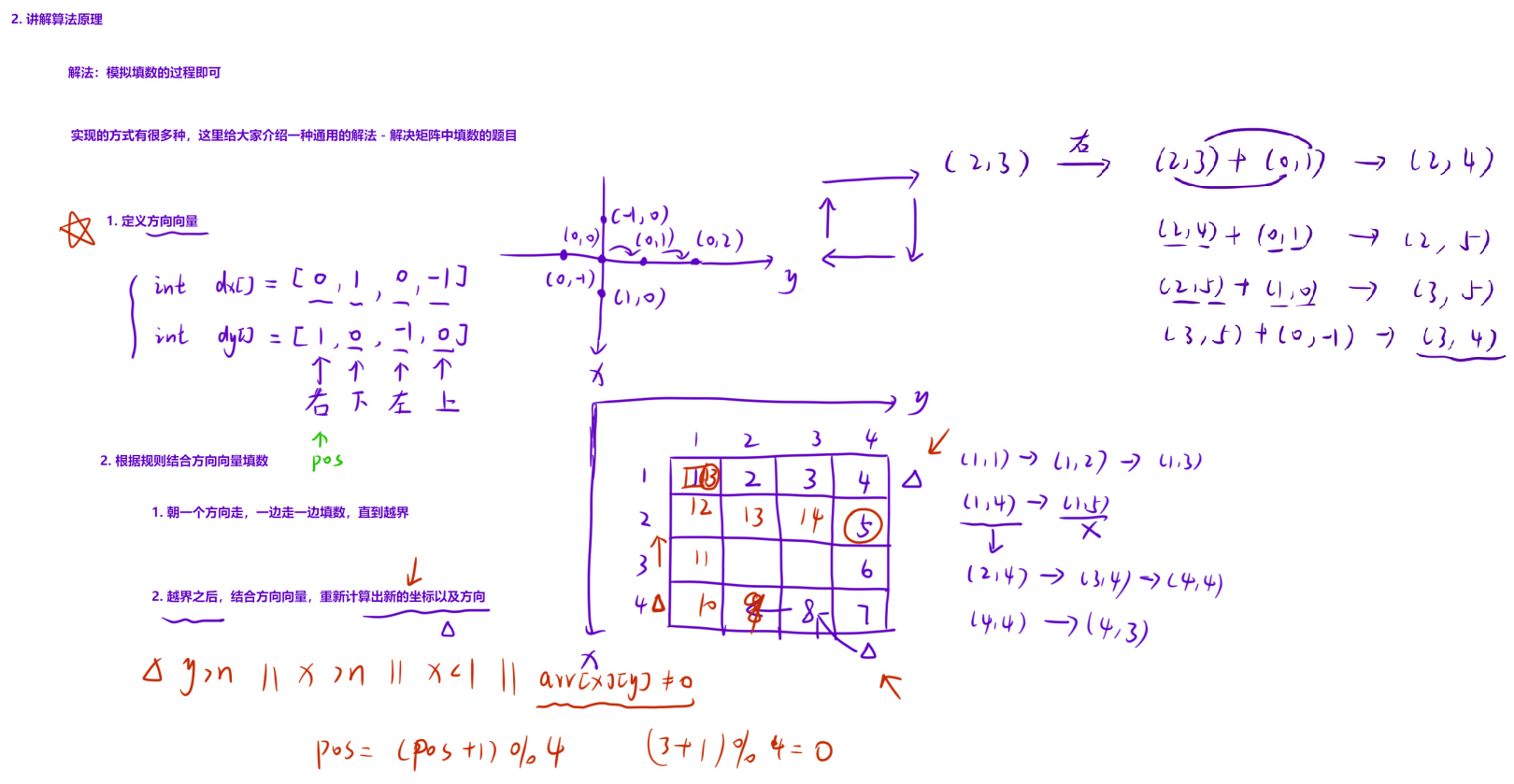
两个数组中每一对下标对应的两个数配套在一起使用就可以实现朝哪个位置偏移一个格子,而且这个顺序和该题目蛇形方阵的顺时针方向是一样的,若有题目是按逆时针排序的话,把数组中对应下标偏移的数据调整下就可以了,图中向量坐标x也y的方向是根据题目定义的,题目是从左上角开始的
补充:这里从下标为1开始处理有效数据是为了方便处理边界情况
#include<iostream>
using namespace std;
const int N = 15;
//定义右,下,左,上四个方向
int dx[] = {0, 1, 0, -1};
int dy[] = {1, 0, -1, 0};
int arr[N][N];//记录矩阵中每个位置的数
int main()
{
int n; cin >> n;
//模拟填数过程
int x = 1, y = 1;//初始位置
int cnt = 1;//当前位置要填的数
int pos = 0;//当前的方向
while(cnt <= n * n)
{
arr[x][y] = cnt;
//计算下一个位置
int a = x + dx[pos], b = y + dy[pos];
//判断是否越界
if(a < 1 || a > n || b < 1 || b > n || arr[a][b])
{
//更新出正确的该走的位置
pos = (pos + 1) % 4;
a = x + dx[pos], b = y + dy[pos];
}
x = a, y = b;
cnt++;
}
//输出
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
printf("%3d", arr[i][j]);
}
puts("");
}
return 0;
}
puts 是 C 语言标准库中的函数,它定义在 <stdio.h> 头文件中,用于输出字符串并自动在末尾添加换行符。
puts 函数用于输出字符串,它的特点是自动在字符串末尾添加换行符。
1.3 字符串的展开
#include<iostream>
#include<algorithm>
using namespace std;
int p1, p2, p3, n;
string s;
string ret;
//判断是否是数字字符
bool isdig(char ch)
{
return ch >= '0' && ch <= '9';
}
//判断是否是小写字母
bool islet(char ch)
{
return ch >= 'a' && ch <= 'z';
}
//将[left, right]之间的字符展开
//left, right这两个字符不做处理
void add(char left, char right)
{
string t;
//遍历中间的字符
for(char ch = left + 1; ch < right; ch++)
{
char tmp = ch;
//处理p1
if(p1 == 2 && islet(tmp)) tmp -= 32;
else if(p1 == 3) tmp = '*';
//处理p2
for(int i = 0; i < p2; i++)
{
//先将展开的字符串放到临时字符串t中
//后面可能逆序,逆序之后再加入ret中
t += tmp;
}
}
//处理p3
if(p3 == 2) reverse(t.begin(), t.end());
ret += t;
}
int main()
{
cin >> p1 >> p2 >> p3 >> s;
int n = s.size();
//循环遍历每一个字符
for(int i = 0; i < n; i++)
{
char ch = s[i];
//减号出现在第一位或最后一位无法展开,也不作处理
if(s[i] != '-' || i == 0 || i == n - 1) ret += ch;
else{
char left = s[i - 1], right = s[i + 1];
//判断是否展开
if(isdig(left) && isdig(right) && right > left ||
islet(left) && islet(right) && right > left)
{
//展开
add(left, right);
}else{
ret += ch;
}
}
}
cout << ret << endl;
return 0;
}代码中没有明确写出(5)对减号右边的字符恰好是左边字符的后继的处理情况,其实是隐含在内的
代码处理逻辑解析
当减号右边的字符是左边字符的后继时(即right = left + 1,如d和e、3和4),代码的处理流程如下:
- 触发条件判断
在主函数的循环中,当遇到中间位置的减号(s[i] = '-'且i不是首尾)时,会先检查左右字符是否满足 “可展开条件”:
- 左右字符同是数字或同是字母;
- 右边字符right严格大于左边字符left(right > left)。
由于 “右边是左边的后继” 满足right = left + 1 > left,且必然同类型(数字或字母),因此会进入 “展开” 分支,执行add(left, right)函数,且不会将减号本身加入结果(ret)。
add函数的核心处理
add函数的作用是生成左右字符之间的展开内容(不包含left和right本身),其关键循环为:
for(char ch = left + 1; ch < right; ch++)当right = left + 1时,循环条件ch < right等价于ch < left + 1,而ch的初始值是left + 1,因此循环不会执行,临时字符串t保持为空。
- 结果拼接
由于t为空,无论p3(逆序)如何设置,t逆序后仍然是空。最终add函数向ret中添加的是空字符串。结合主函数的循环流程:
- 左边字符left在i-1的位置已被加入ret;
- 减号本身不被加入ret;
- 右边字符right在i+1的位置会被加入ret。
因此,left和right会直接拼接,中间没有减号,也没有其他字符,恰好实现了 “删除减号” 的效果。
二、高精度
当数据的值特别大,各种类型都存不下的时候,此时就要用高精度算法来计算加减乘除:
- 先用字符串读入这个数,然后用数组逆序存储该数的每一位;
- 利用数组,模拟加减乘除运算的过程
高精度算法本质上还是模拟算法,用代码模拟小学列竖式计算加减乘除的过程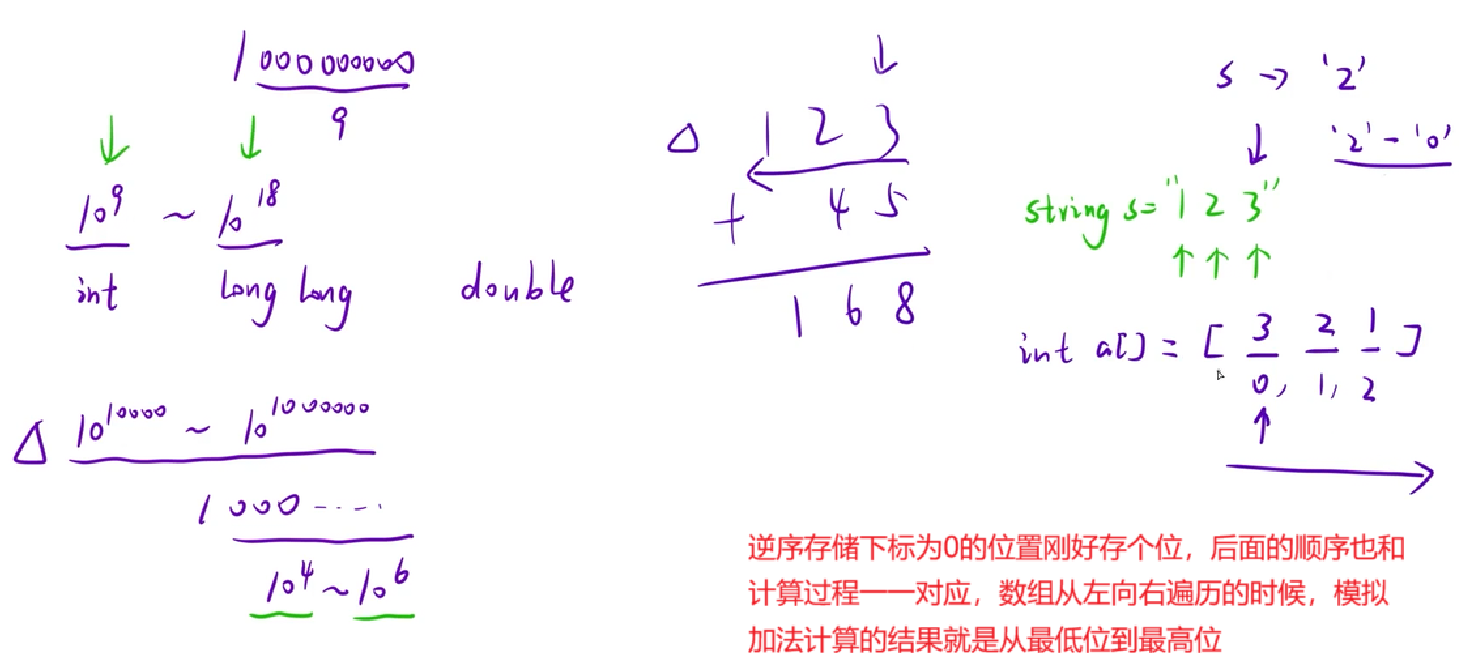
2.1 高精度加法
高精度加法
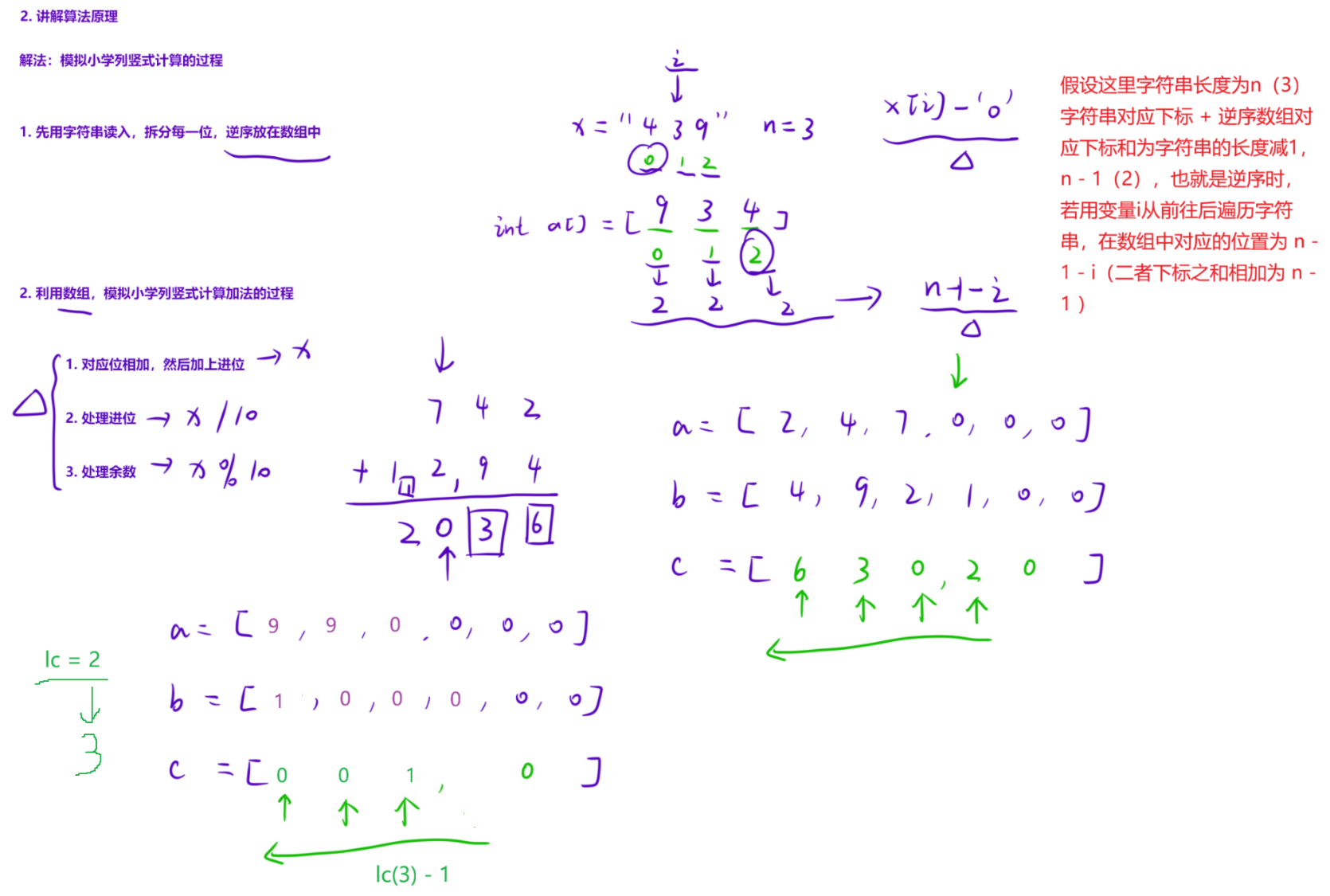
该题目数组数组大小是小于等于500,但是实际情况下高精度加法是可以计算到1e6级别(不会超时),所以这里数组的大小可以扩展到1e6级别
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], b[N], c[N];//第一个数,第二个数,最终结果
int la, lb, lc;//分别标记三个数组中数的长度
void add(int c[], int b[], int a[])
{
for (int i = 0; i < lc; i++)
{
c[i] += a[i] + b[i];//对应位相加 + 进位
c[i + 1] += c[i] / 10;//处理进位
c[i] %= 10;//处理余数
}
//lc的长度有可能是二者长度的最大值 + 1
if (c[lc]) lc++;
}
int main()
{
string x, y; cin >> x >> y;
//拆分每一位,逆序放入数组
la = x.size(); lb = y.size(); lc = max(la, lb);
for (int i = 0; i < la; i++) a[la - 1 - i] = x[i] - '0';
for (int i = 0; i < lb; i++) b[lb - 1 - i] = y[i] - '0';
//模拟手工加法的过程
add(c, b, a);
//逆序输出结果
for (int i = lc - 1; i >= 0; i--) cout << c[i];
return 0;
}
2.2 高精度减法
2.3 高精度乘法
2.4 高精度除法
结语







 浙公网安备 33010602011771号
浙公网安备 33010602011771号