【C++】 STL 详解(十一)之 一棵红黑树模拟map/set - 指南

【C++】 STL 详解(十一)之 一棵红黑树模拟map/set
摘要
本文系统性地介绍了基于红黑树的关联容器实现过程,详细阐述了红黑树节点结构、迭代器设计、平衡调整算法等核心组件的开发,重点分析了map和set容器的封装技术及关键问题的解决方案。
目录
一、库中的 map / set 底层
观察下图源码中的框架,我们进行四点总结:
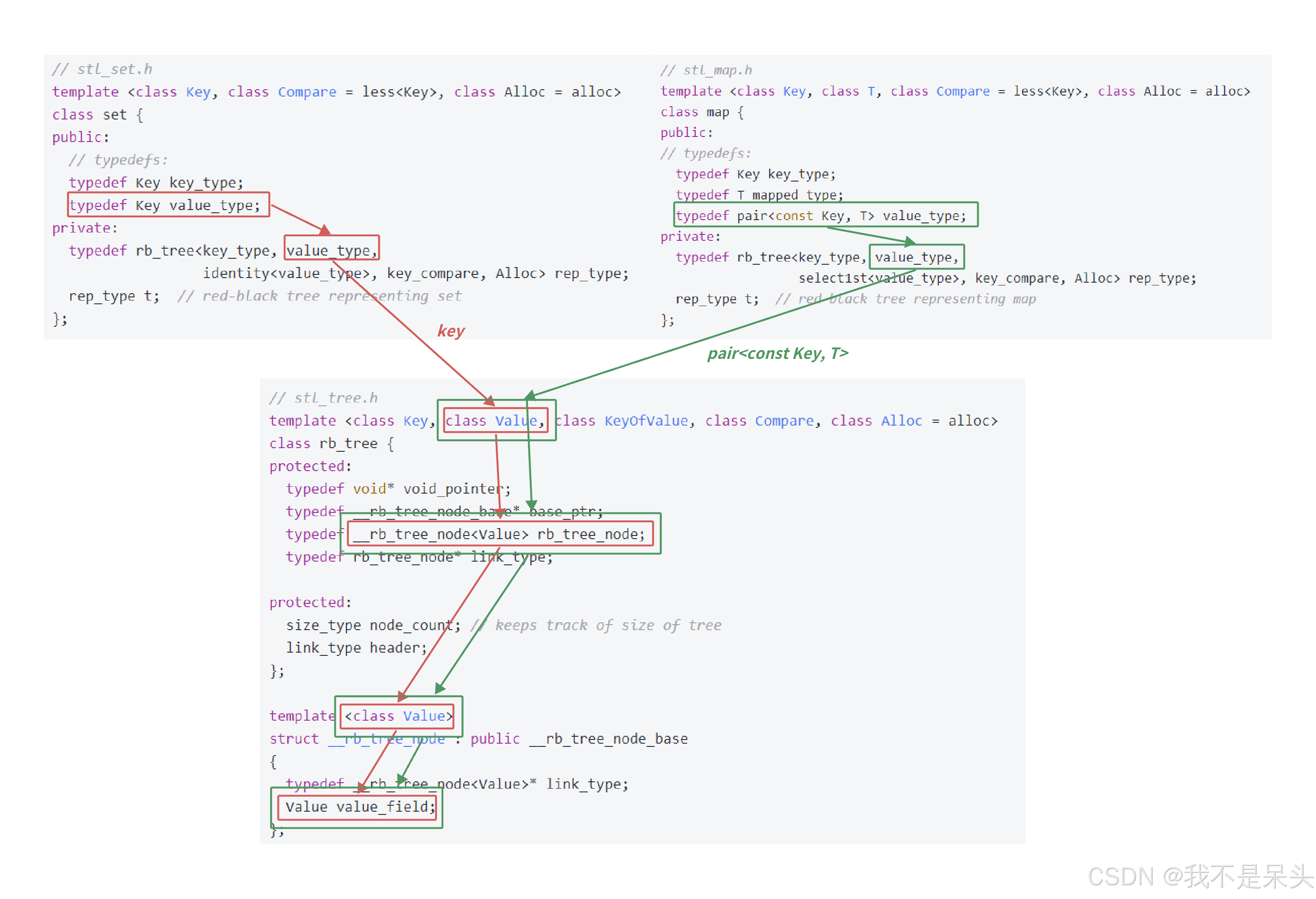
1. 核心设计思想
STL中的红黑树采用了一种巧妙的泛型设计模式,通过模板参数的灵活运用,使得同一棵红黑树既能服务于set的key搜索场景,也能支持map的key/value搜索场景。这种设计的关键在于第二个模板参数Value,它决定了_rb_tree_node中实际存储的数据类型。当set实例化红黑树时,这个参数被指定为key类型;而map实例化时,则传入pair<const key, T>类型。通过这样的参数化设计,红黑树成功实现了代码复用,避免了为不同容器编写重复代码的问题。
2. 模板参数的命名与语义
源码中的命名容易引起理解上的混淆。模板参数通常用T来表示Value,但这里的value_type并不是我们日常理解的key/value结构中的"值",而是指红黑树节点中存储的完整数据类型。对于set来说,value_type就是key本身;对于map来说,value_type则是包含key和value的pair对象。这种命名方式虽然在源码层面有其合理性,但确实需要我们自己去转换思维角度去理解。
3. 双参数设计的必要性
很多人会疑惑:既然第二个模板参数Value已经控制了节点的存储类型,为什么还需要第一个参数Key呢?特别是对于set,两个参数完全相同,看起来似乎冗余。实际上,第一个参数Key主要是为find、erase等查找和删除操作提供函数参数类型。对于set而言,插入和查找都使用相同的key类型,所以两个参数确实重复;但对于map来说,插入操作需要传入pair对象,而查找和删除操作只需要传入key对象,这时两个参数就体现出明显的差异性和必要性了。
4. 代码规范的思考
从命名风格来看,STL源码确实存在一定的不统一性。set使用Key命名模板参数,map使用Key和T的组合,而rb_tree又采用Key和Value的命名方式。这种不一致性说明即使是经验丰富的开发者,在大型项目中也可能出现命名规范不够统一的情况。不过这也提醒我们,在实际开发中更应该注重代码规范和命名一致性,这对代码的可读性和可维护性都有重要影响。
二、模拟实现中参数的控制
1. set.h 于 map.h 的类模板参数
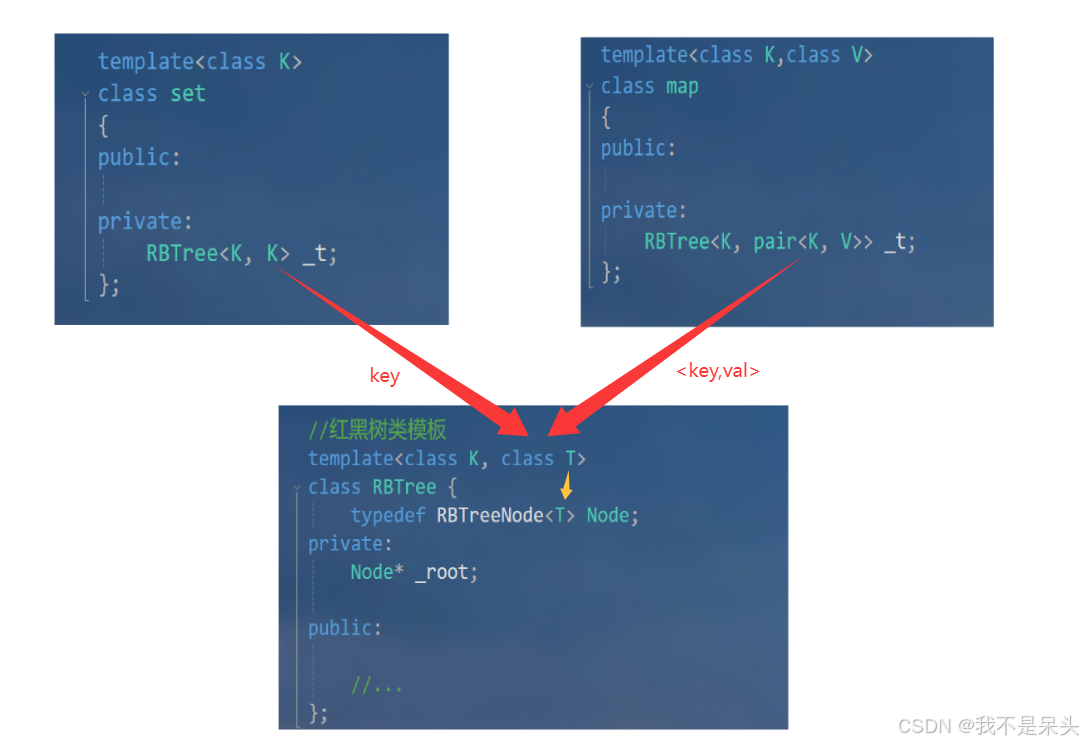
我们都知道,set是K模型的容器,而map是KV模型的容器,那我们如何用一棵KV模型的红黑树同时实现map和set呢?
- 这里我们就需要控制map和set传入底层红黑树的模板参数,为了与原红黑树的模板参数进行区分,我们将红黑树第二个模板参数的名字改为T。
template<class K, class T>
class RBTreeset.h中T模板参数只是键值Key,那么它传入底层红黑树的模板参数就是Key和Key:
template<class K>
class set
{
public:
//...
private:
RBTree<K, K> _t;
};map.hT模板参数是由Key和Value共同构成的键值对,那么它传入底层红黑树的模板参数就是Key以及键值对:
template<class K, class V>
class map
{
public:
//...
private:
RBTree<K, pair<K, V>> _t;
};2. 红黑树节点类模板参数
- 当红黑树模板参数的改变后,红黑树的节点中应该如何储存?
- set容器:K和T都代表键值Key。
- map容器:K代表键值Key,T代表由Key和Value构成的键值对。
- 对于set容器来说,底层红黑树结点当中存储K和T都是一样的,但是对于map容器来说,底层红黑树就只能存储T了。由于底层红黑树并不知道上层容器到底是map还是set,因此红黑树的结点当中直接存储T就行了。
即更改后的红黑树节点类模板为:
//红黑树节点类模板
template<class T>
struct RBTreeNode {
//储存键对值数据
T _data;
//三叉链指针
RBTreeNode<T>* _parent;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
//节点颜色
Color _col;
//构造函数
RBTreeNode(const T& data)
:_data(data)
, _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
//新节点初始颜色为红
, _col(RED)
{}
};三、仿函数增加到模板参数
1. 解释和模板变化
现在由于结点当中存储的是T,这个T可能是Key,也可能是<Key, Value>键值对。那么当我们需要进行结点的键值比较时,应该如何获取结点的键值呢?
当上层容器是set的时候T就是键值Key,直接用T进行比较即可,但当上层容器是map的时候就不行了,此时我们需要从<Key, Value>键值对当中取出键值Key后,再用Key值进行比较。
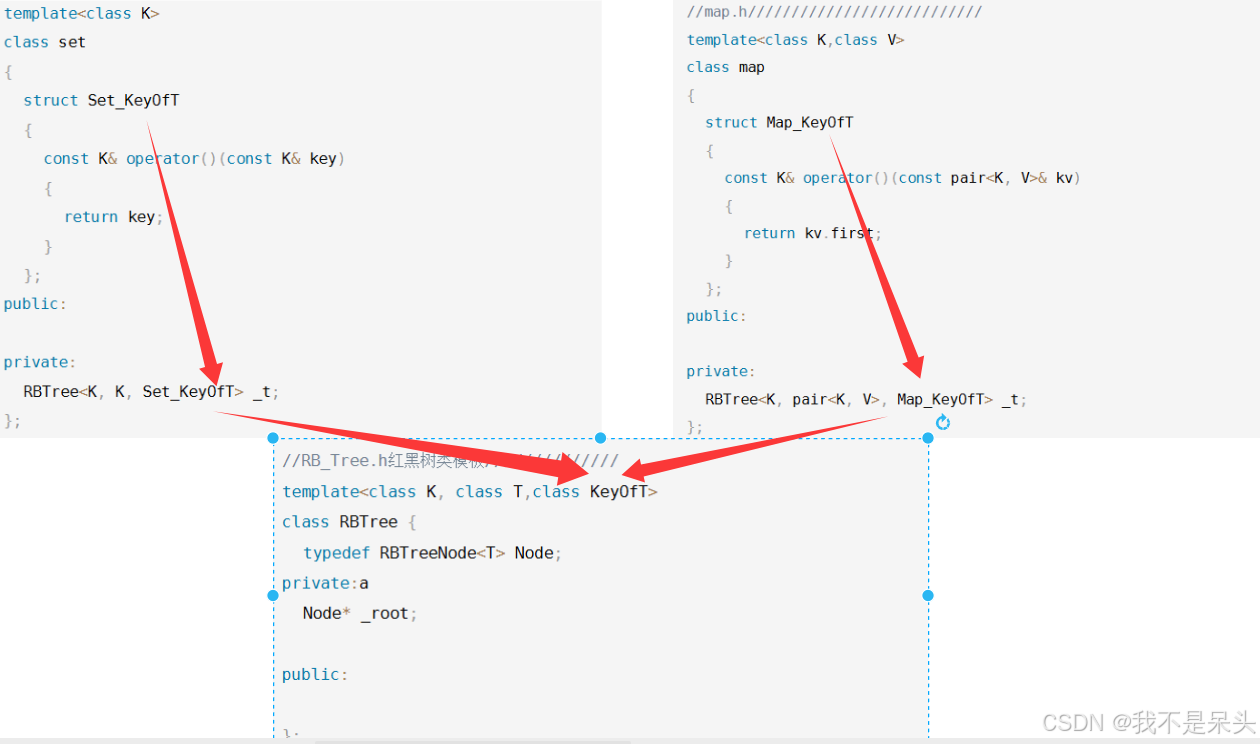
因此,上层容器map需要向底层红黑树提供一个仿函数,用于获取T当中的键值Key,这样一来,当底层红黑树当中需要比较两个结点的键值时,就可以通过这个仿函数来获取T当中的键值了。
仿函数,就是使一个类的使用看上去像一个函数。其实现就是类中实现一个operator(),这个类就有了类似函数的行为,就是一个仿函数类了。
但是对于底层红黑树来说,它并不知道上层容器是map还是set,因此当需要进行两个结点键值的比较时,底层红黑树都会通过传入的仿函数来获取键值Key,进而进行两个结点键值的比较。
因此,set容器也需要向底层红黑树传入一个仿函数,虽然这个仿函数单独看起来没什么用,但却是必不可少的。
//RB_Tree.h红黑树类模板//////////////
template<class K, class T,class KeyOfT>
class RBTree {
typedef RBTreeNode<T> Node;
private:a
Node* _root;
public:
};
//set.h/////////////////////////
template<class K>
class set
{
struct Set_KeyOfT
{
const K& operator()(const K& key)
{
return key;
}
};
public:
private:
RBTree<K, K, Set_KeyOfT> _t;
};
//map.h///////////////////////////
template<class K,class V>
class map
{
struct Map_KeyOfT
{
const K& operator()(const pair<K, V>& kv)
{
return kv.first;
}
};
public:
private:
RBTree<K, pair<K, V>, Map_KeyOfT> _t;
};
2. 查找函数为例
这样一来,当底层红黑树需要进行两个结点之间键值的比较时,都会通过传入的仿函数来获取相应结点的键值,然后再进行比较,下面以红黑树的查找函数为例(实现在红黑树类中):
//查找函数
iterator Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (key < tok(cur->_data)) //key值小于该结点的值
{
cur = cur->_left; //在该结点的左子树当中查找
}
else if (key > tok(cur->_data)) //key值大于该结点的值
{
cur = cur->_right; //在该结点的右子树当中查找
}
else //找到了目标结点
{
return iterator(cur); //返回该结点
}
}
return end(); //查找失败
}三、红黑树迭代器模拟实现
1. 正向迭代器模拟实现
迭代器的基本设计框架
红黑树迭代器的实现思路与list迭代器本质相同,都是通过封装节点指针并重载相关运算符来实现类似指针的访问行为。核心思想是用一个类包装节点指针,然后通过运算符重载让这个对象能够像原生指针一样使用。但红黑树迭代器的特殊之处在于,它需要按照中序遍历的顺序访问节点,这使得operator++和operator–的实现成为整个迭代器设计中最具挑战性的部分。
- 我们通过一个结点的指针便可以构造出一个正向迭代器。
- 当对正向迭代器进行解引用操作时,我们直接返回对应结点数据的引用即可。
- 当对正向迭代器进行->操作时,我们直接返回对应结点数据的指针即可。
- 当然,正向迭代器当中至少还需要重载==和!=运算符,实现时直接判断两个迭代器所封装的结点是否是同一个即可。
| 参数 | 作用 | 普通迭代器的值 | 常量迭代器的值 |
|---|---|---|---|
| T | 节点数据类型 | int 或 pair<const K, V> | int 或 pair<const K, V> |
| Ref | operator*返回类型 | T& | const T& |
| Ptr | operator->返回类型 | T* | const T* |
// 红黑树迭代器类模板
template<class T, class Ref, class Ptr>
struct RBTree_iterator {
typedef RBTreeNode<T> Node;
typedef RBTree_iterator <T, Ref, Ptr> Self;
// ✅ 添加这两个typedef供反向迭代器使用
typedef Ref reference;
typedef Ptr pointer;
Node* _node; // 封装节点指针
// 构造函数
RBTree_iterator(Node* node)
: _node(node)
{}
// 解引用运算符:让迭代器像指针一样访问数据
Ref operator*() {
return _node->_data;
}
// 箭头运算符:支持 it->first 这样的访问
Ptr operator->() {
return &(_node->_data);
}
// 不等于运算符:用于判断迭代器是否相等
bool operator!=(const Self& s) const {
return _node != s._node;
}
// 等于运算符
bool operator==(const Self& s) const {
return _node == s._node;
}
// 后续实现operator++和operator--
};中序遍历的起点与终点
map和set的迭代器遵循中序遍历规则,访问顺序是左子树、根节点、右子树。因此begin()返回的迭代器指向中序遍历的第一个节点,也就是整棵树最左下角的节点。比如在一棵包含10到50的树中,begin()会指向值为10的节点。理解这个起点对于后续实现operator++的逻辑至关重要,因为所有的递增操作都是基于中序遍历的顺序进行的。
// 在红黑树类中实现begin()和end()
template<class K, class T, class KeyOfT>
class RBTree {
public:
typedef RBTree_iterator<T, T&, T*> iterator;
typedef RBTree_iterator<T, const T&, const T*> const_iterator;
// begin()返回中序遍历的第一个节点(最左节点)
iterator begin() {
Node* leftmost = _root;
if (leftmost == nullptr) {
return iterator(nullptr);
}
// 一直向左走到底
while (leftmost->_left) {
leftmost = leftmost->_left;
}
return iterator(leftmost);
}
// const版本的begin()
const_iterator begin() const {
Node* leftmost = _root;
if (leftmost == nullptr) {
return const_iterator(nullptr);
}
while (leftmost->_left) {
leftmost = leftmost->_left;
}
return const_iterator(leftmost);
}
// end()返回nullptr表示结束
iterator end() {
return iterator(nullptr);
}
const_iterator end() const {
return const_iterator(nullptr);
}
};operator++的核心实现逻辑
实现迭代器自增运算符的关键在于"局部思维",不要试图从全局角度看整棵树,而是只关注当前节点的局部环境,思考中序遍历下一个应该访问哪个节点。这种局部化的思考方式大大简化了实现的复杂度。
右子树非空的情况 - 当当前节点的右子树存在时,说明当前节点已经访问完毕,按照中序遍历规则,接下来应该访问右子树。而右子树的中序第一个节点就是它的最左节点。因此这种情况下,只需要进入右子树,然后一直向左走到底,找到最左节点即可。
右子树为空的情况 - 当当前节点的右子树为空时,情况会复杂一些。这意味着不仅当前节点访问完了,当前节点所在的整个子树也访问完了。此时需要访问的下一个节点一定在当前节点到根的路径上的某个祖先节点中。我们需要沿着父指针向上查找,寻找满足特定条件的祖先节点。
向上查找的判断条件 - 在向上查找过程中需要判断当前节点是其父节点的左孩子还是右孩子。如果当前节点是父节点的左孩子,根据中序遍历的"左子树-根节点-右子树"规则,那么父节点就是下一个要访问的节点。举个例子,如果迭代器指向25,而25的右子树为空且25是30的左孩子,那么下一个访问的就是30。
如果当前节点是父节点的右孩子,说明不仅当前节点所在的子树访问完了,父节点及其左子树也都访问完了。这时需要继续向上查找,直到找到一个节点,它是其父节点的左孩子为止。比如迭代器指向15,15是10的右孩子,需要继续向上,10是18的左孩子,所以下一个访问的节点是18。
//前置++
Self& operator++()
{
if (_node->_right)
{
Node* leftmost = _node->_right;
while (leftmost->_left)
{
leftmost = leftmost->_left;
}
_node = leftmost;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}end()的表示方法
当迭代器指向最后一个节点(中序遍历的最右节点)时,再执行++操作会遇到一个特殊情况。以50为例,它是40的右孩子,40是30的右孩子,30是18的右孩子,而18已经是根节点没有父节点了。在这种情况下找不到符合条件的祖先节点,父指针最终会变成nullptr。我们可以用nullptr来表示end(),这是一种简洁的实现方式。需要注意的是,STL源码中使用了一个哨兵头节点来表示end(),这个哨兵节点与根节点互为父节点,它的左指针指向最左节点,右指针指向最右节点。虽然我们采用nullptr的方案与STL略有不同,但在功能上完全等价,该实现的功能都能实现。
// 测试代码示例
void TestIterator() {
RBTree<int, int, SetKeyOfT> tree;
tree.Insert(18);
tree.Insert(10);
tree.Insert(30);
tree.Insert(15);
tree.Insert(50);
// 正向遍历
auto it = tree.begin();
while (it != tree.end()) {
cout << *it << " ";
++it; // 当it指向50时,++it会让_node变成nullptr
}
// 输出: 10 15 18 30 50
// end()返回nullptr
auto endIt = tree.end();
// endIt._node == nullptr
}operator--的实现思路
迭代器的自减运算符实现逻辑与自增完全对称,只是方向相反。因为反向遍历的顺序是右子树、根节点、左子树。如果当前节点的左子树不为空,下一个访问的节点是左子树的最右节点。如果左子树为空,需要向上查找,直到找到一个节点是其父节点的右孩子。
//前置--
Self& operator--()
{
if (_node->_left)
{
Node* rightmost = _node->_left;
while (rightmost->_right)
{
rightmost = rightmost->_right;
}
_node = rightmost;
}
else
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}实际上,上述所实现的迭代器是有缺陷的,因为理论上我们对end()位置的正向迭代器进行--操作后,应该得到最后一个结点的正向迭代器,但我们实现end()时,是直接返回由nullptr构造得到的正向迭代器的,因此上述实现的代码无法完成此操作。
下面我们来看看C++SLT库当中的实现逻辑: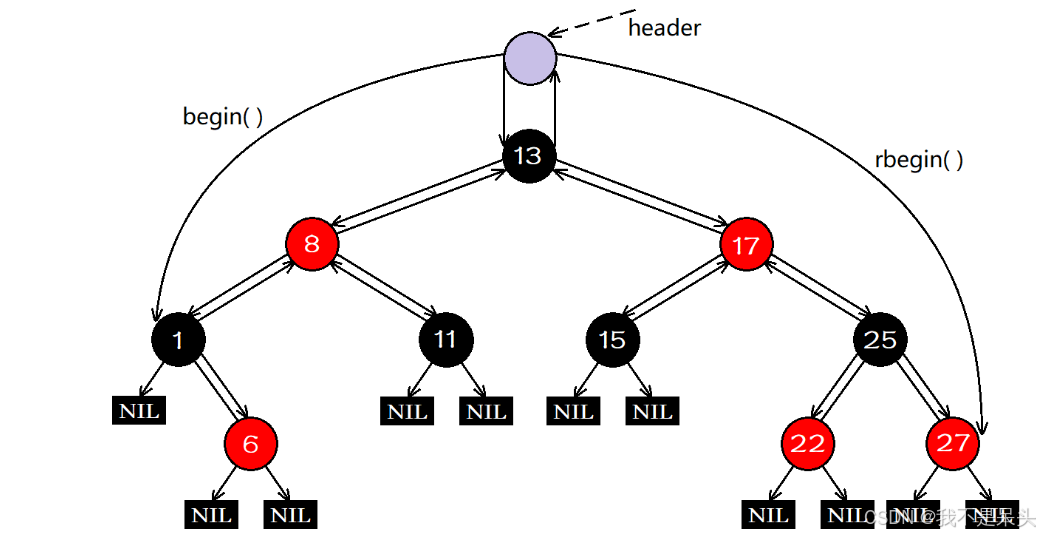
C++STL库当中实现红黑树时,在红黑树的根结点处增加了一个头结点,该头结点的左指针指向红黑树当中的最左结点,右指针指向红黑树当中的最右结点,父指针指向红黑树的根结点。
在该结构下,实现begin()时,直接用头结点的左孩子构造一个正向迭代器即可,实现rbegin()时,直接用头结点的右孩子构造一个反向迭代器即可(实际是先用该结点构造一个正向迭代器,再用正向迭代器构造出反向迭代器),而实现end()和rend()时,直接用头结点构造出正向和反向迭代器即可。此后,通过对逻辑的控制,就可以实现end()进行–操作后得到最后一个结点的正向迭代器。
但实现该结构需要更改当前很多函数的逻辑,例如插入结点时,若插入到了红黑树最左结点的左边,或最右结点的右边,此时需要更新头结点左右指针的指向。
2. 反向迭代器的使用
//反向迭代器
template<class Iterator>
struct ReverseIterator
{
typedef ReverseIterator<Iterator> Self;
typedef typename Iterator::reference Ref; // ✅ 现在可以正常使用了
typedef typename Iterator::pointer Ptr;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{
}
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
bool operator!=(const Self& s) const
{
return _it != s._it;
}
bool operator==(const Self& s) const
{
return _it == s._it;
}
};需要注意的是,反向迭代器只接收了一个模板参数,即正向迭代器的类型,也就是说,反向迭代器不知道结点的引用类型和结点的指针类型,因此我们需要在正向迭代器当中对这两个类型进行typedef,这样反向迭代器才能通过正向迭代器获取结点的引用类型和结点的指针类型。
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode<T> Node; //结点的类型
public:
typedef ReverseIterator<iterator> reverse_iterator; //反向迭代器
reverse_iterator rbegin()
{
//寻找最右结点
Node* rightmost = _root;
while (rightmost && rightmost->_right)
{
rightmost = rightmost->_right;
}
//返回最右结点的反向迭代器
return reverse_iterator(iterator(rightmost));
}
reverse_iterator rend()
{
//返回由nullptr构造得到的反向迭代器(不严谨)
return reverse_iterator(iterator(nullptr));
}
// const版本
const_reverse_iterator rbegin() const
{
Node* rightmost = _root;
if (rightmost == nullptr)
{
return rend();
}
while (rightmost->_right)
{
rightmost = rightmost->_right;
}
return const_reverse_iterator(const_iterator(rightmost));
}
const_reverse_iterator rend() const
{
return const_reverse_iterator(const_iterator(nullptr));
}
private:
Node* _root; //红黑树的根结点
};常量迭代器的实现
不同容器对迭代器的修改权限有不同要求。对于set,它的迭代器不应该支持修改元素,因为修改key会破坏红黑树的有序性。实现方法是在set实例化红黑树时,将第二个模板参数改为const K,即RBTree<K, const K, SetKeyOfT> _t。这样通过迭代器访问的数据类型就是const K,自然无法修改。
// set的实现
template<class K>
class set {
struct SetKeyOfT {
const K& operator()(const K& key) {
return key;
}
};
public:
// 注意第二个参数是const K,这样迭代器就无法修改元素
typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;
typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;
private:
RBTree<K, const K, SetKeyOfT> _t;
public:
iterator begin() {
return _t.begin();
}
iterator end() {
return _t.end();
}
// 使用示例
pair<iterator, bool> insert(const K& key) {
return _t.Insert(key);
}
};
// 测试set迭代器
void TestSet() {
set<int> s;
s.insert(10);
s.insert(5);
s.insert(15);
auto it = s.begin();
// *it = 20; // 编译错误!因为返回的是const int&
cout << *it << endl; // 可以读取,输出5
}对于map,情况稍微复杂一些。map的迭代器不能修改key,但应该允许修改value,因为value的变化不会影响树的结构。实现方法是在map实例化红黑树时,将pair的第一个参数声明为const,即RBTree<K, pair<const K, V>, MapKeyOfT> _t。这样key被const保护无法修改,而value仍然可以修改,完美满足了map的使用需求。
// map的实现
template<class K, class V>
class map {
struct MapKeyOfT {
const K& operator()(const pair<const K, V>& kv) {
return kv.first;
}
};
public:
// 注意pair的第一个参数是const K
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;
private:
RBTree<K, pair<const K, V>, MapKeyOfT> _t;
public:
iterator begin() {
return _t.begin();
}
iterator end() {
return _t.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv) {
return _t.Insert(kv);
}
};
// 测试map迭代器
void TestMap() {
map<int, string> m;
m.insert(make_pair(1, "apple"));
m.insert(make_pair(2, "banana"));
m.insert(make_pair(3, "cherry"));
auto it = m.begin();
// it->first = 10; // 编译错误!first是const的
it->second = "orange"; // 正确!可以修改value
cout << it->first << ":" << it->second << endl; // 输出 1:orange
}四、源码
1. set.h
#pragma once
#include"Rb_tree.h"
template<class K>
class set
{
struct SetKeyOfT // ✅ 统一命名(去掉下划线)
{
const K& operator()(const K& key) const // ✅ 建议添加const
{
return key;
}
};
public:
// ✅ 统一使用 SetKeyOfT,第二个参数用 const K
typedef typename RBTree<K, const K, SetKeyOfT>::iterator iterator;
typedef typename RBTree<K, const K, SetKeyOfT>::const_iterator const_iterator;
typedef typename RBTree<K, const K, SetKeyOfT>::reverse_iterator reverse_iterator;
typedef typename RBTree<K, const K, SetKeyOfT>::const_reverse_iterator const_reverse_iterator;
iterator begin() {
return _t.begin();
}
iterator end() {
return _t.end();
}
const_iterator begin() const {
return _t.begin();
}
const_iterator end() const {
return _t.end();
}
reverse_iterator rbegin() {
return _t.rbegin();
}
reverse_iterator rend() {
return _t.rend();
}
const_reverse_iterator rbegin() const {
return _t.rbegin();
}
const_reverse_iterator rend() const {
return _t.rend();
}
//插入函数
pair<iterator, bool> insert(const K& key)
{
return _t.Insert(key);
}
//删除函数
void erase(const K& key)
{
_t.Erase(key);
}
//查找函数
iterator find(const K& key)
{
return _t.Find(key);
}
const_iterator find(const K& key) const
{
return _t.Find(key);
}
private:
// ✅ 与typedef保持一致,第二个参数用 const K
RBTree<K, const K, SetKeyOfT> _t;
};2. map.h
#pragma once
#include"Rb_tree.h"
template<class K, class V>
class map
{
struct MapKeyOfT // ✅ 统一命名
{
const K& operator()(const pair<const K, V>& kv) const // ✅ 参数类型匹配
{
return kv.first;
}
};
public:
// ✅ 统一使用 MapKeyOfT 和一致的pair类型
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::reverse_iterator reverse_iterator;
typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::const_reverse_iterator const_reverse_iterator;
iterator begin() {
return _t.begin();
}
iterator end() {
return _t.end();
}
const_iterator begin() const {
return _t.begin();
}
const_iterator end() const {
return _t.end();
}
reverse_iterator rbegin() {
return _t.rbegin();
}
reverse_iterator rend() {
return _t.rend();
}
const_reverse_iterator rbegin() const {
return _t.rbegin();
}
const_reverse_iterator rend() const {
return _t.rend();
}
//插入函数
pair<iterator, bool> insert(const pair<const K, V>& kv)
{
return _t.Insert(kv);
}
//[]运算符重载函数
V& operator[](const K& key)
{
pair<iterator, bool> ret = insert(make_pair(key, V()));
return ret.first->second;
}
//删除函数
void erase(const K& key)
{
_t.Erase(key);
}
//查找函数
iterator find(const K& key)
{
return _t.Find(key);
}
const_iterator find(const K& key) const
{
return _t.Find(key);
}
private:
// ✅ 与typedef保持一致
RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};3. Rb_Tree.h
#pragma once
#include<iostream>
#include<utility>
using namespace std;
//使用枚举类定义节点颜色
enum Color {
RED,
BLACK
};
//红黑树节点类模板
template<class T>
struct RBTreeNode {
T _data;
RBTreeNode<T>* _parent;
RBTreeNode<T>* _left;
RBTreeNode<T>* _right;
Color _col;
RBTreeNode(const T& data)
:_data(data)
, _parent(nullptr)
, _left(nullptr)
, _right(nullptr)
, _col(RED)
{}
};
//红黑树迭代器
template<class T, class Ref, class Ptr>
struct RBTree_iterator {
typedef RBTreeNode<T> Node;
typedef RBTree_iterator<T, Ref, Ptr> Self;
// ✅ 添加这两个typedef供反向迭代器使用
typedef Ref reference;
typedef Ptr pointer;
Node* _node;
RBTree_iterator(Node* node = nullptr)
:_node(node)
{}
Ref operator*()
{
return _node->_data;
}
Ptr operator->()
{
return &(_node->_data);
}
bool operator!=(const Self& s) const
{
return _node != s._node;
}
bool operator==(const Self& s) const
{
return _node == s._node;
}
//前置++
Self& operator++()
{
if (_node->_right)
{
Node* leftmost = _node->_right;
while (leftmost->_left)
{
leftmost = leftmost->_left;
}
_node = leftmost;
}
else
{
Node* cur = _node;
Node* parent = cur->_parent;
while (parent && cur == parent->_right)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
//后置++
Self operator++(int)
{
Self tmp(*this);
++(*this);
return tmp;
}
//前置--
Self& operator--()
{
if (_node->_left)
{
Node* rightmost = _node->_left;
while (rightmost->_right)
{
rightmost = rightmost->_right;
}
_node = rightmost;
}
else
{
Node* cur = _node;
Node* parent = _node->_parent;
while (parent && cur == parent->_left)
{
cur = parent;
parent = cur->_parent;
}
_node = parent;
}
return *this;
}
//后置--
Self operator--(int)
{
Self tmp(*this);
--(*this);
return tmp;
}
};
//反向迭代器
template<class Iterator>
struct ReverseIterator
{
typedef ReverseIterator<Iterator> Self;
typedef typename Iterator::reference Ref; // ✅ 现在可以正常使用了
typedef typename Iterator::pointer Ptr;
Iterator _it;
ReverseIterator(Iterator it)
:_it(it)
{
}
Ref operator*()
{
return *_it;
}
Ptr operator->()
{
return _it.operator->();
}
Self& operator++()
{
--_it;
return *this;
}
Self& operator--()
{
++_it;
return *this;
}
bool operator!=(const Self& s) const
{
return _it != s._it;
}
bool operator==(const Self& s) const
{
return _it == s._it;
}
};
//红黑树类模板
template<class K, class T, class KeyOfT>
class RBTree {
typedef RBTreeNode<T> Node;
public:
typedef RBTree_iterator<T, T&, T*> iterator;
typedef RBTree_iterator<T, const T&, const T*> const_iterator;
typedef ReverseIterator<iterator> reverse_iterator; //反向迭代器
typedef ReverseIterator<const_iterator> const_reverse_iterator;
private:
Node* _root;
public:
RBTree()
:_root(nullptr)
{}
//查找函数
iterator Find(const K& key)
{
KeyOfT kot; // ✅ 创建对象实例
Node* cur = _root;
while (cur)
{
if (key < kot(cur->_data))
{
cur = cur->_left;
}
else if (key > kot(cur->_data))
{
cur = cur->_right;
}
else
{
return iterator(cur);
}
}
return end();
}
const_iterator Find(const K& key) const
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (key < kot(cur->_data))
{
cur = cur->_left;
}
else if (key > kot(cur->_data))
{
cur = cur->_right;
}
else
{
return const_iterator(cur);
}
}
return end();
}
//begin()返回中序遍历的第一个节点
iterator begin()
{
Node* leftmost = _root;
if (leftmost == nullptr)
{
return iterator(nullptr);
}
while (leftmost->_left)
{
leftmost = leftmost->_left;
}
return iterator(leftmost);
}
const_iterator begin() const
{
Node* leftmost = _root;
if (leftmost == nullptr)
{
return const_iterator(nullptr);
}
while (leftmost->_left)
{
leftmost = leftmost->_left;
}
return const_iterator(leftmost);
}
//end()返回nullptr表示结束
iterator end()
{
return iterator(nullptr);
}
const_iterator end() const
{
return const_iterator(nullptr);
}
reverse_iterator rbegin()
{
//寻找最右结点
Node* rightmost = _root;
while (rightmost && rightmost->_right)
{
rightmost = rightmost->_right;
}
//返回最右结点的反向迭代器
return reverse_iterator(iterator(rightmost));
}
reverse_iterator rend()
{
//返回由nullptr构造得到的反向迭代器(不严谨)
return reverse_iterator(iterator(nullptr));
}
// const版本
const_reverse_iterator rbegin() const
{
Node* rightmost = _root;
if (rightmost == nullptr)
{
return rend();
}
while (rightmost->_right)
{
rightmost = rightmost->_right;
}
return const_reverse_iterator(const_iterator(rightmost));
}
const_reverse_iterator rend() const
{
return const_reverse_iterator(const_iterator(nullptr));
}
//插入函数
pair<iterator, bool> Insert(const T& data)
{
KeyOfT kot; // ✅ 创建仿函数对象
if (_root == nullptr)
{
_root = new Node(data);
_root->_col = BLACK;
return make_pair(iterator(_root), true);
}
else
{
Node* parent = nullptr;
Node* cur = _root;
//找插入位置
while (cur != nullptr)
{
if (kot(data) > kot(cur->_data))
{
parent = cur;
cur = cur->_right;
}
else if (kot(data) < kot(cur->_data))
{
parent = cur;
cur = cur->_left;
}
else
{
return make_pair(iterator(cur), false);
}
}
//创建新节点
cur = new Node(data);
Node* newnode = cur;
cur->_col = RED;
cur->_parent = parent;
//与父节点链接
if (kot(cur->_data) > kot(parent->_data))
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
// ✅ 完整的调整红黑树平衡代码
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (parent->_left == cur)
{
RotateR(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
else
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = BLACK;
uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else
{
if (parent->_right == cur)
{
RotateL(grandfather);
parent->_col = BLACK;
grandfather->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = RED;
}
break;
}
}
}
_root->_col = BLACK;
return make_pair(iterator(newnode), true);
}
}
private:
//右单旋
void RotateR(Node* parent)
{
Node* ppnode = parent->_parent;
Node* cur = parent->_left;
Node* curR = cur->_right;
parent->_left = curR;
if (curR) { curR->_parent = parent; }
cur->_right = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
}
//左单旋
void RotateL(Node* parent)
{
Node* ppnode = parent->_parent;
Node* cur = parent->_right;
Node* curL = cur->_left;
parent->_right = curL;
if (curL) { curL->_parent = parent; }
cur->_left = parent;
parent->_parent = cur;
if (ppnode == nullptr)
{
_root = cur;
cur->_parent = nullptr;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
cur->_parent = ppnode;
}
else
{
ppnode->_right = cur;
cur->_parent = ppnode;
}
}
}
};test.c
#include <iostream>
#include <string>
#include "map.h"
#include "set.h"
using namespace std;
void TestMap()
{
cout << "========== Test Map ==========" << endl;
map<string, int> m;
// 测试插入
m.insert(make_pair("apple", 5));
m.insert(make_pair("banana", 3));
m.insert(make_pair("orange", 8));
m.insert(make_pair("grape", 2));
// 测试operator[]
m["pear"] = 4;
m["apple"] = 10; // 修改已存在的值
// 正向遍历
cout << "Forward traversal:" << endl;
for (auto it = m.begin(); it != m.end(); ++it)
{
cout << it->first << " : " << it->second << endl;
}
cout << endl;
// 反向遍历
cout << "Reverse traversal:" << endl;
for (auto it = m.rbegin(); it != m.rend(); ++it)
{
cout << it->first << " : " << it->second << endl;
}
cout << endl;
// 测试查找
auto found = m.find("banana");
if (found != m.end())
{
cout << "Found banana: " << found->second << endl;
}
// 测试不存在的key
if (m.find("watermelon") == m.end())
{
cout << "watermelon not found" << endl;
}
cout << endl;
}
void TestSet()
{
cout << "========== Test Set ==========" << endl;
set<int> s;
// 测试插入
s.insert(5);
s.insert(2);
s.insert(8);
s.insert(1);
s.insert(9);
s.insert(3);
// 正向遍历
cout << "Forward traversal:" << endl;
for (auto it = s.begin(); it != s.end(); ++it)
{
cout << *it << " ";
}
cout << endl << endl;
// 反向遍历
cout << "Reverse traversal:" << endl;
for (auto it = s.rbegin(); it != s.rend(); ++it)
{
cout << *it << " ";
}
cout << endl << endl;
// 测试查找
auto found = s.find(8);
if (found != s.end())
{
cout << "Found 8 in set" << endl;
}
// 测试不存在的元素
if (s.find(100) == s.end())
{
cout << "100 not found in set" << endl;
}
cout << endl;
}
void TestDuplicate()
{
cout << "========== Test Duplicate Insert ==========" << endl;
map<int, string> m;
set<int> s;
// 测试重复插入
auto result1 = m.insert(make_pair(1, "one"));
auto result2 = m.insert(make_pair(1, "ONE")); // 重复key
cout << "Map insert result: " << result1.second << " (first time)" << endl;
cout << "Map insert result: " << result2.second << " (second time)" << endl;
cout << "Value for key 1: " << m.find(1)->second << endl;
auto result3 = s.insert(100);
auto result4 = s.insert(100); // 重复元素
cout << "Set insert result: " << result3.second << " (first time)" << endl;
cout << "Set insert result: " << result4.second << " (second time)" << endl;
cout << endl;
}
int main()
{
TestMap();
TestSet();
TestDuplicate();
cout << "All tests completed!" << endl;
return 0;
}总结
通过完整的代码实现和测试验证,成功构建了符合STL标准的map和set容器,证明了红黑树在关联容器中的高效性和可靠性,为理解STL底层数据结构提供了有价值的实践参考。
✨ 坚持用 清晰易懂的图解 + 代码语言, 让每个知识点都 简单直观 !
个人主页 :不呆头 · CSDN
代码仓库 :不呆头 · Gitee
专栏系列 :座右铭 : “不患无位,患所以立。”





 浙公网安备 33010602011771号
浙公网安备 33010602011771号