详细介绍：多尺度与细节增强的Segment Anything模型用于显著目标检测

摘要

显著目标检测（SOD）旨在识别和分割图像中最突出的目标。先进的SOD方法通常利用各种卷积神经网络（CNN）或Transformer进行深度特征提取。然而，这些手段在困难情况下仍然表现不佳且泛化能力差。最近，Segment Anything Model（SAM）作为一种视觉基础模型被提出，具有强大的分割和泛化能力。尽管如此，SAM需要目标对象的精确提示，这在SOD中是不可用的。此外，SAM缺乏对多尺度和多级信息的利用，以及对细粒度细节的整合。为了解决这些缺点，我们提出了一个用于SOD的多尺度和细节增强SAM（MDSAM）。具体而言，我们开始引入了一个轻量级多尺度适配器（LMSA），它允许SAM以极少的可训练参数学习多尺度信息。然后，我们提出了一个多级融合模块（MLFM），以全面利用SAM编码器的多级信息。最后，我们提出了一个细节增强模块（DEM），将SAM与细粒度细节相结合。实验结果证明了我们的模型在多个SOD数据集上的卓越性能及其在其他分割任务上的强大泛化能力。源代码发布在https://github.com/BellyBeauty/MDSAM

关键词

显著目标检测，Segment Anything模型，多尺度特征提取，目标细节增强

1 引言

显著目标检测（SOD）旨在识别和分割图像中最突出的目标。作为一项基础任务，SOD在许多下游任务中发挥着重要作用，如目标跟踪[68, 5]、场景分割[51, 6]、行人重识别[13, 41]等。在过去十年中，卷积神经网络（CNN）在SOD领域取得了巨大进展。然而，SOD需要全局上下文信息，这对于CNN来说由于其有限的感受野而具有挑战性。幸运的是，由于自注意力的全局感知能力，Vision Transformer（ViT）[8]极大地促进了SOD的发展。然而，由于训练样本不足和域差距大，这些SOD方式在复杂情况下仍然表现不佳且泛化能力差。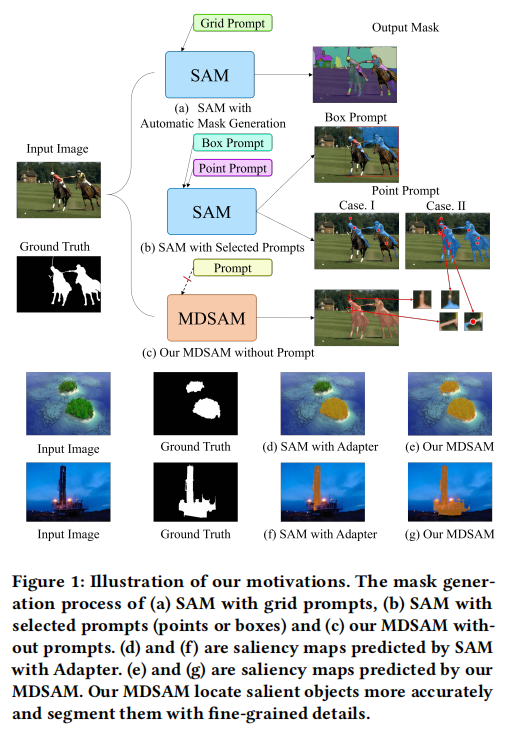

将SAM适应到SOD的直接方法。然而，它可能导致巨大的训练参数，甚至导致性能下降。先前的工作已经运用适配器[18]将这些基础模型迁移到下游任务。尽管如此，如图1(d)所示，使用适配器训练的SAM在多尺度场景中表现不佳。此外，SAM仅使用图像编码器末尾的特征，导致低级信息的丢失。如图1(d)和(f)所示，由于缺乏多尺度信息和细粒度细节，SAM会遇到不完整的对象掩码和不准确的对象边缘。就是最近，一个名为Segment Anything Model（SAM）[23]的视觉基础模型被提出用于通用图像分割。SAM受益于超过10亿个训练样本，这使其在许多分割任务中具有强大的泛化能力[4, 35, 42, 60, 72]。然而，为了实现鲁棒的分割，SAM需要手工设计的提示，如点、框或对应于感兴趣对象的粗略掩码。如图1(a)所示，采用网格提示的SAM能够自动生成目标掩码。然而，这些掩码是类别无关的，无法识别显著目标。如图1(b)所示，点提示需要准确的数量和关键点的位置。因此，即使有轻微的差异也会导致错误的结果。同时，框提示在几个具有挑战性的场景中可能无效，如目标遮挡。因此，将SAM适应到SOD需要为显著目标精心选择提示。这对于SOD来说是不合适的，缘于在推理过程中真实标签是不可用的。事实上，完全微调

为了解决上述问题，我们提出了一种名为多尺度和细节增强SAM（MDSAM）的新框架，用于高性能SOD。功能上，它通过多尺度和细节增强信息将SAM适应到SOD任务。具体来说，我们起初提出了一个轻量级多尺度适配器（LMSA），以非常少的参数将SAM适应到SOD，同时提取多尺度信息。随后，我们提出了一个多级融合模块（MLFM），以提取和融合SAM编码器不同级别的特征。最后，我们提出了一个细节增强模块（DEM），结合图像细节和边缘进行SOD预测，这有助于生成精确和详细的分割结果。大量实验表明，我们的模型不仅在SOD上表现良好，而且在其他分割任务上也表现出卓越的性能。

我们的首要贡献总结如下：
• 我们提出了一个名为多尺度和细节增强SAM（MDSAM）的新框架，用于高性能SOD。
• 我们提出了一个轻量级多尺度适配器（LMSA），以将SAM适应到SOD，同时保持训练效率和强大的泛化能力。
• 我们提出了多级融合模块（MLFM）和细节增强模块（DEM），分别提高SAM的多尺度和细粒度感知能力。
• 大家进行了大量实验，验证了我们的方法在多个SOD素材集和其他分割任务上的卓越有效性和强大泛化能力。

2 相关工作

2.1 显著目标检测

目前，SOD途径大致分为两类：基于CNN的方法和基于Transformer的方法。基于CNN的方法通常采用深度CNN，如VGGNet[43]、ResNet[15]作为骨干网络来提取和融合多尺度特征。例如，Zhang等人[70]提出聚合多级卷积特征进行SOD。Zhang等人[71]提出学习不确定卷积特征以完成准确的SOD。Wang等人[49]提出了一种分阶段优化CNN模型来检测图像中的显著目标。此外，Zhang等人[67]利用孪生CNN学习无损特征反射，用于结构感知的SOD。Wu等人[56]提出了一种级联部分解码器，用于快速准确的SOD。Zeng等人[64]提出了一种全局-局部CNN，融合深度特征进行高分辨率SOD。Wei等人[54]提出了一种融合-反馈-聚焦策略，以提高多级特征表示能力。Mohammadi等人[37]引入了内容感知引导用于SOD。Liu等人[29]提出了一种动态特征集成，用于同时检测显著目标、边缘和骨架。Zhao等人[74]提出了一种简单门控CNN，抑制无关特征并平衡SOD的信息。Pang等人[39]引入了一种多尺度交互网络，以提高特征效率和预测一致性。Wei等人[55]提出解耦SOD标签，以改善主体和细节感知。Wang等人[52]提出了一种多级增强SOD技巧，通过集成像素、区域和对象。

尽管这些办法在SOD方面取得了巨大进展，但它们仍然表现不令人满意。主要原因是CNN本质上缺乏全局感知能力，这对于SOD极其重要。

，它们在复杂情况下泛化能力较差。在这项工作中，大家借鉴了视觉基础模型的卓越特征提取和泛化能力，并将它们迁移到SOD任务中，以获得更好的性能。就是最近，由于自注意力的全局感知能力，ViT[8]在SOD任务中显示出卓越的有效性。为了利用ViT的优势，Liu等人[31]应用T2T-ViT[62]捕获长距离依赖关系并集成多级特征，以获得更好的SOD结果。Yun等人[63]提出了一种具有金字塔Transformer的自优化网络，以增强显著目标的全局语义和局部细节信息。Zhuge等人[78]利用Swin Transformer[32]提取多尺度特征并增强检测到的显著区域的完整性。Wang等人[53]结合多个Transformer学习局部-全局表示，用于基于涂鸦的RGB-D SOD。Deng等人[6]引入了一种递归多尺度Transformer，用于高分辨率SOD。尽管这些基于Transformer的途径表现令人印象深刻，但它们缺乏对目标细节的细粒度感知。更重要的

2.2 Segment Anything模型

最近，SAM[23]被提出作为一种视觉基础模型，用于通用图像分割。经过适当的修改，它在许多下游任务中表现非常出色[4, 35, 42, 60, 72]。然而，SAM需目标的精确提示，如点、框或掩码。这些提示对于SOD来说很难获得。一些工作已经对SAM进行了完全微调，以便将其迁移到SOD任务。然而，完全微调将导致过多的训练参数，甚至导致性能下降。同时，有些工作试图用少量可训练参数迁移SAM。例如，Cui等人[5]提出启用SAM的低秩适应（LoRA）进行SOD。Xu等人[58]引入了SAM的多维探索，用于弱监督SOD。Ke等人[22]设计了一种可学习的高质量输出令牌，它被注入到SAM的掩码解码器中，负责预测高质量掩码。尽管有效，但这些方式未能使SAM学习多尺度和多级信息。此外，SAM的简单解码器无法整合详细信息，导致分割不准确。为了处理这些问题，大家提出了LMSA，用非常少的训练参数将SAM迁移到SOD，并使SAM获得多尺度信息。此外，我们引入了轻量级模块，利用细粒度细节以获得更好的SOD性能。

3 我们提出的方法

在这项工作中，我们提出了一种新颖的多尺度和细节增强SAM（MDSAM）用于SOD任务。图2显现了整体架构，它为SAM配备了三个新颖模块：轻量级多尺度适配器（LMSA）、多级融合模块（MLFM）和细节增强模块（DEM）。我们将在以下部分中描述它们。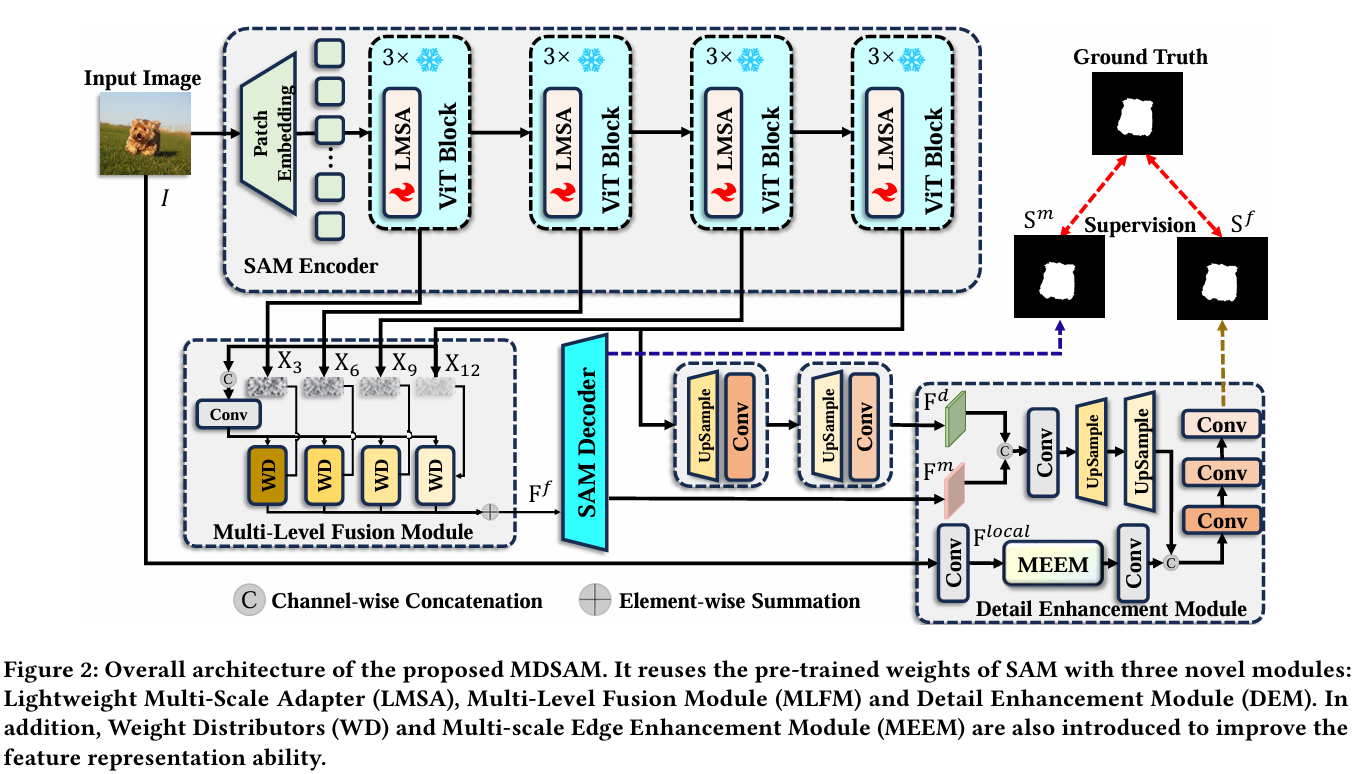

3.1 轻量级多尺度适配器

第一个将多尺度适配器应用于将SAM迁移到下游任务的。我们通过增强提取局部信息的能力进行了进一步改进。这样，我们的MDSAM重用并保留了SAM的预训练权重，同时以非常少的训练参数整合了多尺度信息。就是尽管SAM在许多分割任务中表现良好，但提供适当提示的挑战仍然限制了其在SOD中的直接应用。一个可能的解决方案是对SAM进行完全微调。然而，SAM编码器的过多可训练参数和不足的SOD数据可能导致不满意的表现。幸运的是，适配器[18]是一种有效的方法，可以用很少的训练参数将SAM适应到SOD。此外，多尺度信息对SOD非常有帮助。为此，我们提出了一个轻量级多尺度适配器（LMSA），将SAM适应到SOD。据我们所知，我们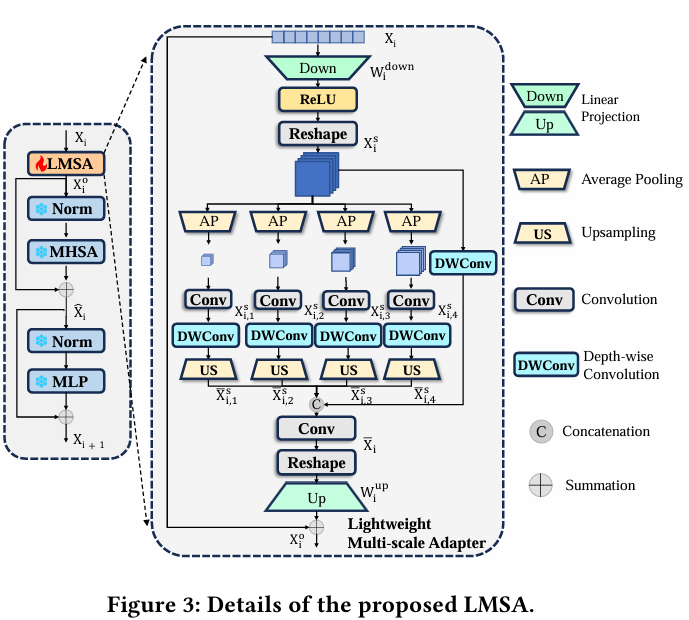

如图3所示，SAM编码器的每个Transformer层由多头自注意力（MHSA）[47]、多层感知机（MLP）和两个归一化层组成。它表示如下：
$$\begin{array}{rl}& {\hat{\mathbf{X}}}_i=MHSA(LN({\mathbf{X}}_i))+{\mathbf{X}}_i,\\ & {\mathbf{X}}_{i+1}=MLP(LN({\hat{\mathbf{X}}}_i))+{\hat{\mathbf{X}}}_i,\end{array}$$
其中${\mathbf{X}}_i\in {\mathbb{R}}^{N\times D}$是第i个Transformer层的输出。N是令牌的数量。D是嵌入维度。${\hat{\mathbf{X}}}_i\in {\mathbb{R}}^{N\times D}$是中间输出。LN表示层归一化（LN）[1]。为了将SAM适应到SOD，大家在每个Transformer层中的第一个归一化之前使用所提出的LMSA。

LMSA的详细结构如图3所示。具体来说，我们最初使用线性投影层来降低特征维度：
$${\mathbf{X}}_i^s=\tau (ReLU({\mathbf{W}}_i^{down}({\mathbf{X}}_i))),$$
其中${\mathbf{W}}_i^{down}\in {\mathbb{R}}^{D\times \frac{D}{r}}$是线性投影层的参数。在ReLU激活函数之后，我们将特征重塑为${\mathbf{X}}_i^s\in {\mathbb{R}}^{\frac{D}{r}\times W\times H}$，以便进一步进行空间信息处理。$[\cdot ]$缩减因子。就是是重塑处理。r

然后，为了提高表示能力，大家使用四个平均池化（AP）层来获取多尺度特征${\mathbf{X}}_{i,j}^s\in {\mathbb{R}}^{\frac{D}{4\times r}\times W_j\times H_j}$，并利用深度卷积层捕获局部细节信息：
$${\mathbf{X}}_{i,j}^s={\varphi }_{1\times 1}(AP({\mathbf{X}}_i^s)),1\le j\le 4,$$
$${\bar{\mathbf{X}}}_{i,j}^s=US(DWConv({\mathbf{X}}_{i,j}^s)),$$
其中${\varphi }_{1\times 1}$定义了一个带有1×1核的卷积层，后跟GELU函数[16]。DWConv是一个带有3×3核和GELU函数的深度卷积层。US是双线性插值，用于将特征上采样到特定分辨率。

之后，我们将多尺度特征${\bar{\mathbf{X}}}_{i,j}^s\in {\mathbb{R}}^{\frac{D}{r}\times W\times H}$与${\mathbf{X}}_i^s$融合如下：
$${\bar{\mathbf{X}}}_i={\varphi }_{1\times 1}([{\bar{\mathbf{X}}}_{i,1}^s,{\bar{\mathbf{X}}}_{i,2}^s,{\bar{\mathbf{X}}}_{i,3}^s,{\bar{\mathbf{X}}}_{i,4}^s,DWConv({\mathbf{X}}_i^s)]),$$
其中${\bar{\mathbf{X}}}_i\in {\mathbb{R}}^{\frac{D}{r}\times W\times H}$，$[\cdot ]$是通道级联。

最后，大家将${\bar{\mathbf{X}}}_i$重塑回令牌化特征。通过线性投影层和残差连接[15]，我们获得LMSA的最终输出：
$${\bar{\mathbf{X}}}_i^o={\mathbf{W}}_i^{up}\left(\tau \right({\bar{\mathbf{X}}}_i\left)\right)+{\mathbf{X}}_i,$$
其中${\mathbf{W}}_i^{up}\in {\mathbb{R}}^{\frac{D}{r}\times D}$是一个线性投影层，用于恢复特征维度。

通过LMSA，SAM允许以非常少的训练参数适应SOD任务。此外，与其他手段相比，我们的方式可以更好地利用多尺度信息，从而使模型学习更好的特征。

3.2 多级融合模块

在SAM编码器中，每一层囊括不同的信息。浅层囊括更多的低级细节信息，而深层包含更丰富的高级语义信息。在SOD任务中，仅依靠深层的高级信息可能无法在复杂情况下准确定位目标。因此，利用多级信息对SOD是必要的。然而，SAM仅使用编码器最后一层的输出作为掩码解码器的输入。此外，方便的级联融合策略无法充分整合来自不同层的多级信息[70]。为了解决这个问题，我们提出了一个多级融合模块（MLFM），以全面利用SAM编码器的多级信息。如图4所示，所提出的MLFM生成权重并将它们分配给不同层，使用权重分配器（WD）。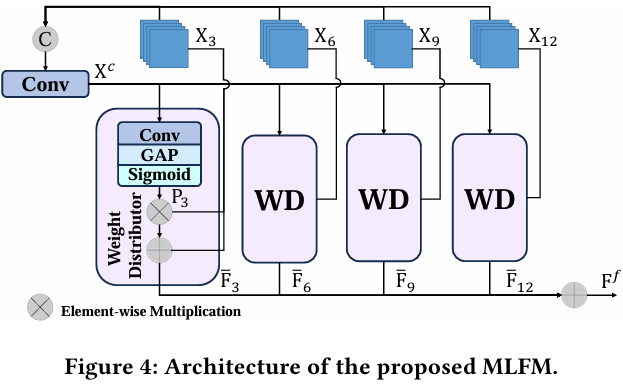

我们将SAM编码器中不同层的输出特征表示为${\mathbf{X}}_q\in {\mathbb{R}}^{D\times H\times W}(q=3,6,9,12)$。首先，大家连接它们并通过卷积层获得聚合特征${\mathbf{X}}^c$：
$${\mathbf{X}}^c={\varphi }_{1\times 1}([{\mathbf{X}}_3,{\mathbf{X}}_6,{\mathbf{X}}_9,{\mathbf{X}}_{12}]).$$
随后，我们基于${\mathbf{X}}^c$获得权重${\mathbf{P}}_q$并将它们分配给不同层，如下所示：
$$\begin{array}{rl}& {\mathbf{P}}_q=\delta (GAP({\varphi }_{1\times 1}({\mathbf{X}}^c))),\\ & {\bar{\mathbf{F}}}_q={\mathbf{P}}_q\times {\mathbf{X}}_q+{\mathbf{X}}_q,\end{array}$$
其中$\delta$表示Sigmoid函数。GAP是全局平均池化（GAP）。最后，我们获得融合特征${\mathbf{F}}^f\in {\mathbb{R}}^{D\times H\times W}$如下：
$${\mathbf{F}}^f={\Sigma }_q{\bar{\mathbf{F}}}_q.$$
经过MLFM后，${\mathbf{F}}^f$将用作掩码解码器的图像嵌入。与原始SAM不同，我们提出的MLFM的输出特征充分融合了SAM编码器的多级信息。

3.3 细节增强模块

在LMSA和MLFM的协助下，我们的框架充分利用了多尺度和多级信息。这极大地援助了SAM在SOD任务中的应用。然而，仍然存在一些剩余障碍。一方面，SAM编码器采用图像块嵌入策略，不可避免地会丢失细节信息。另一方面，SAM解码器中的上采样策略无法恢复关键细节。因此，具有复杂细节和边缘的显著目标没有被充分捕获。为了解决这个问题，我们提出了一个细节增强模块（DEM），以增强细粒度细节，获得更好的SOD性能。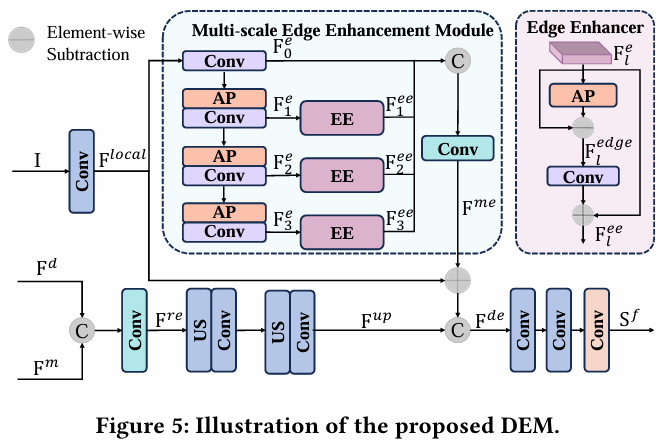

如图5所示，所提出的DEM包括主分支和辅助分支。主分支将掩码解码器的特征从输出逐步上采样到输入分辨率。辅助分支从输入图像中提取细粒度细节信息，并将其添加到主分支的特征中。然而，直接在输入分辨率下提取细节会导致计算量过大，减慢推理速度。因此，大家提出了一个多尺度边缘增强模块（MEEM）。在MEEM中，我们使用3×3平均池化和1×1卷积来提取细节信息。此外，我们利用边缘增强器（EE）来突出特征图中目标的边缘。

从技术上讲，在主分支中，大家最初连接掩码解码器特征${\mathbf{F}}^m$和SAM编码器最后一层上采样后的特征${\mathbf{F}}^d$。然后，我们使用1×1卷积层来减少通道维度。最后，我们应用多个双线性插值和3×3卷积将特征逐步上采样到输入分辨率：
$$\begin{array}{c}{\mathbf{F}}^{re}={\varphi }_{1\times 1}([{\mathbf{F}}^d,{\mathbf{F}}^m]),\\ {\mathbf{F}}^{up}={\varphi }_{3\times 3}(U{S}_{\times 2}({\varphi }_{3\times 3}(U{S}_{\times 2}({\mathbf{F}}^{re}))))\end{array}$$
其中$U{S}_{\times 2}$是运用双线性插值的2倍上采样。${\varphi }_{3\times 3}$包含一个带有3×3核的卷积层、批归一化和ReLU函数。

尽管${\mathbf{F}}^{up}$可用于SOD预测，但它缺乏细节和边缘信息。因此，大家引入辅助分支并提出MEEM，从输入图像中整合细粒度细节。具体来说，给定输入图像I，我们首先应用3×3卷积层提取局部特征：
$${\mathbf{F}}^{local}={\varphi }_{3\times 3}(\mathbf{I}),$$
其中${\mathbf{F}}^{local}\in {\mathbb{R}}^{C\times H\times W}$。通过所提出的MEEM，我们从图像中在多个尺度上提取边缘信息，并进一步增强显著目标的边缘感知。为了减少计算复杂度，我们使用平均池化来扩大感受野。MEEM的过程如下：
$${\mathbf{F}}_0^e={\varphi }_{1\times 1}({\mathbf{F}}^{local}),$$
$${\mathbf{F}}_{t+1}^e=AP({\varphi }_{1\times 1}^{\prime }({\mathbf{F}}_t^e)),(0\le t\le 2),$$
其中$AP$表示带有3×3核的平均池化。${\varphi }_{1\times 1}^{\prime }$表示一个带有批归一化和Sigmoid函数的1×1卷积层。${\mathbf{F}}_t^e\in {\mathbb{R}}^{C\times H\times W}$是在尺度t的特征。然后，大家引入边缘增强器$\psi$来增强每个尺度上的细节信息：
$${\mathbf{F}}_l^{ee}=\psi ({\mathbf{F}}_l^e),(1\le l\le 3),$$
其中${\mathbf{F}}_l^{ee}\in {\mathbb{R}}^{C\times H\times W}$是边缘增强特征。边缘增强器的结构如图5右上部分所示，可以表示如下：
$${\mathbf{F}}_l^{edge}={\mathbf{F}}_l^e-AP({\mathbf{F}}_l^e),$$
$${\mathbf{F}}_l^{ee}={\varphi }_{1\times 1}^{\prime }({\mathbf{F}}_l^{edge})+{\mathbf{F}}_l^e,$$
其中${\mathbf{F}}_l^{edge}\in {\mathbb{R}}^{C\times H\times W}$。之后，我们通过通道级联和1×1卷积层融合这些特征：
$${\mathbf{F}}^{me}={\varphi }_{1\times 1}([{\mathbf{F}}_0^e,{\mathbf{F}}_1^{ee},{\mathbf{F}}_2^{ee},{\mathbf{F}}_3^{ee}]),$$
其中${\mathbf{F}}^{me}\in {\mathbb{R}}^{C\times H\times W}$是MEEM的输出特征。这样，${\mathbf{F}}^{me}$既包含细粒度细节，也具备多尺度边缘信息。我们使用这些特征来补充${\mathbf{F}}^c$中缺失的信息。经过级联后，我们应用两个3×3卷积层和一个1×1卷积层来获得最终的SOD结果${\mathbf{S}}^f$：
$${\mathbf{F}}^{de}=[{\mathbf{F}}^{up},{\mathbf{F}}^{me}+{\mathbf{F}}^{local}],$$
$$\begin{array}{r}{\mathbf{S}}^f={\varphi }_{1\times 1}({\varphi }_{3\times 3}({\varphi }_{3\times 3}({\mathbf{F}}^{de}))).\end{array}$$
可以看出，在MEEM的协助下，我们的DEM可以从输入图像中提取多尺度边缘，并将它们与主分支结合。借助利用两个分支，SAM中缺乏细节的问题得到了解决。因此，我们的MDSAM能够奏效地定位具有丰富细节信息的显著目标。

3.4 损失函数

为了训练大家的框架，我们引入了二元交叉熵（BCE）损失、交并比（IoU）损失和L1损失。为了提高学习能力，我们将其应用于${\mathbf{S}}^f$和${\mathbf{S}}^m={\varphi }_{1\times 1}({\mathbf{F}}^m)$。MDSAM的总损失公式如下：
$$\mathcal{L}(\mathbf{S},{\mathbf{S}}^{gt})={\mathcal{L}}_{BCE}+{\mathcal{L}}_{IoU}+{\mathcal{L}}_{L1},$$
$${\mathcal{L}}_{total}={\mathcal{L}}_f({\mathbf{S}}^f,{\mathbf{S}}^{gt})+{\mathcal{L}}_m({\mathbf{S}}^m,{\mathbf{S}}^{gt}),$$
其中${\mathbf{S}}^{gt}$是显著目标的真实标签。

4 实验

4.1 实验设置

数据集。为了公平比较，我们在DUTS-TR[48]（10533张图像）上训练我们提出的MDSAM，并在五个SOD基准数据集上评估它，包括DUTS-TE[48]（5019张图像）、DUTS-OMRON[61]（5168张图像）、HKU-IS[26]（4447张图像）、ECSSD[59]（1000张图像）和PASCAL-S[28]（850张图像）。

评估指标。按照先前的工作，我们采用四个广泛使用的指标来评估SOD性能，即平均绝对误差（MAE）[40]、最大F-measure$(F_{\beta }^{max})$[61]、S-measure$(S_m)$[9]和平均增强对齐度量$(E_m)$[10]。

实现细节。我们使用PyTorch工具箱在NVIDIA A100 GPU上实现我们的办法。对于初始化，我们从SAM-B模型加载图像编码器和掩码解码器的权重。我们提出的MDSAM的其余部分随机初始化。我们将图像调整为512×512和384×384作为输入，并将批量大小分别设置为16和32。我们使用AdamW优化器进行训练，权重衰减为$1e^{-4}$。在训练期间，我们冻结SAM的编码器，并将学习率设置为$5e^{-5}$用于其余预训练权重。对于我们提出的模块，我们将学习率设置为$5e^{-4}$。大家采用5个epoch的预热期，并训练到最大80个epoch。

4.2 与最先进方法的比较

我们将我们提出的MDSAM与15个其他模型进行比较，包括CPD[56]、F3Net[54]、CAGNet[37]、DFI[29]、GateNet[74]、MINet[39]、LDF[55]、ICON[78]、TE[25]、MENet[52]、VST[31]、SelfReformer[63]、DC-Net[77]、BBRF[36]、SAM[23]。注意，SAM保持原始结构并为SOD进行完全微调。为了公平比较，显著图要么由作者提供，要么由他们发布的预训练模型生成。所有指标都使用相同的工具计算。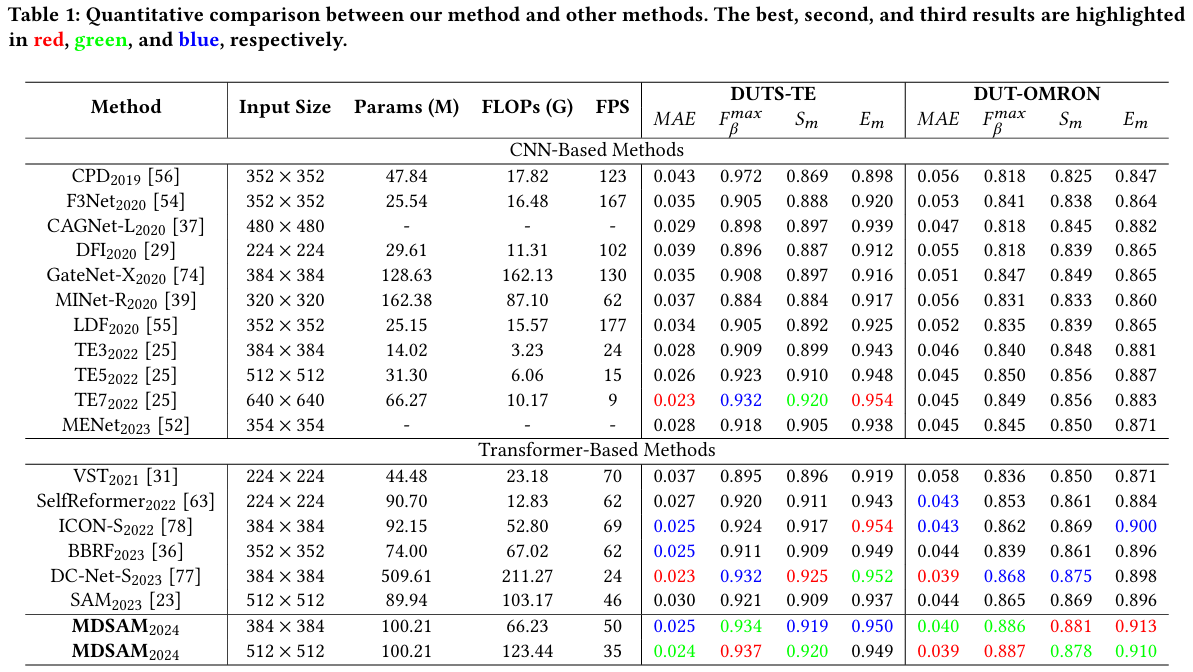

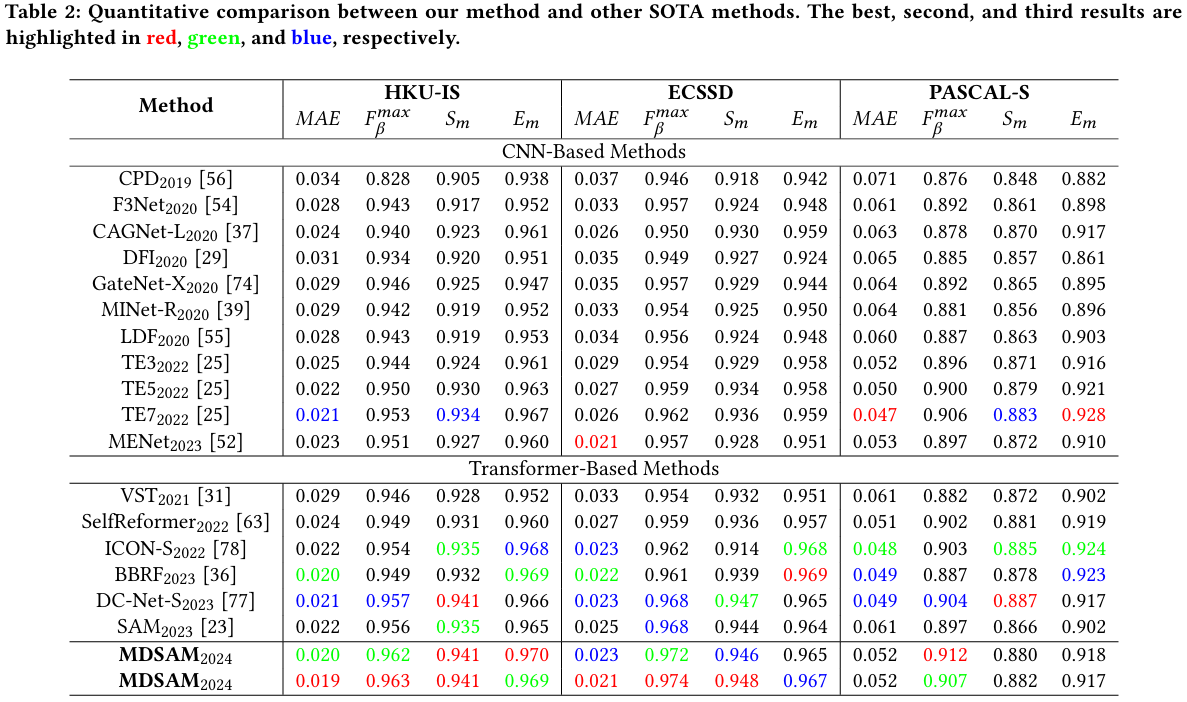
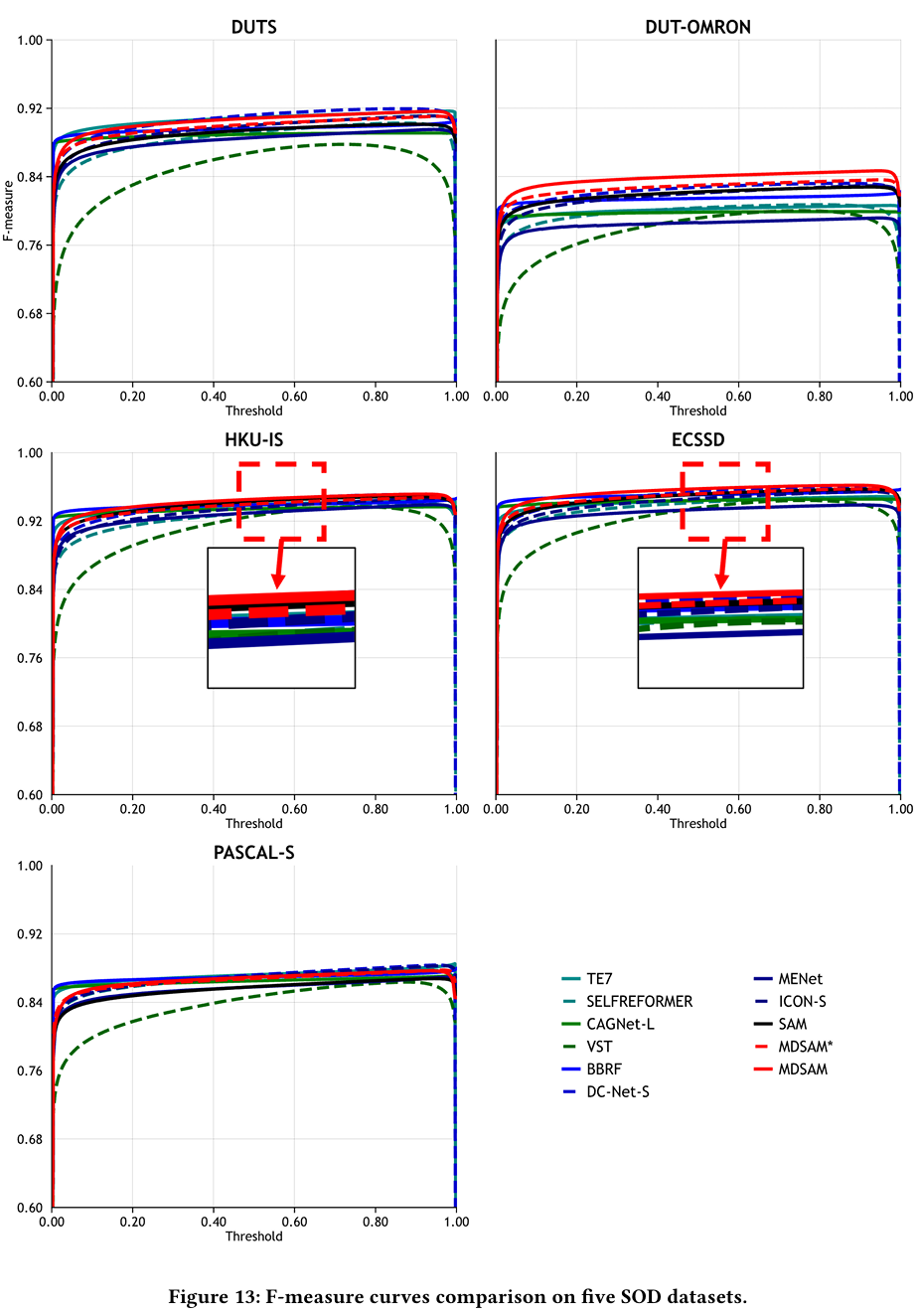
定量评估。表1和表2显示了比较方式的定量结果。我们提出的输入分辨率为512×512的MDSAM在DUTS-OMRON、HKU-IS和ECSSD上取得了最佳结果。此外，我们的MDSAM在DUTS上也表现出高度竞争力。尽管我们的MDSAM在PASCAL-S数据集上表现较差，但它获得了最佳的总体结果。在384×384输入分辨率下，我们的MDSAM在相似分辨率下获得了最佳的总体性能。在表1和表2中，SAM在512×512分辨率下进行完全微调。可以观察到，与原始SAM相比，我们的MDSAM显著提高了性能，同时略微增加了模型参数。在相同分辨率下，我们的MDSAM的推理速度仅略有下降。此外，当我们的MDSAM以384×384分辨率推理时，它在推理速度和准确性方面都优于512×512分辨率的SAM。

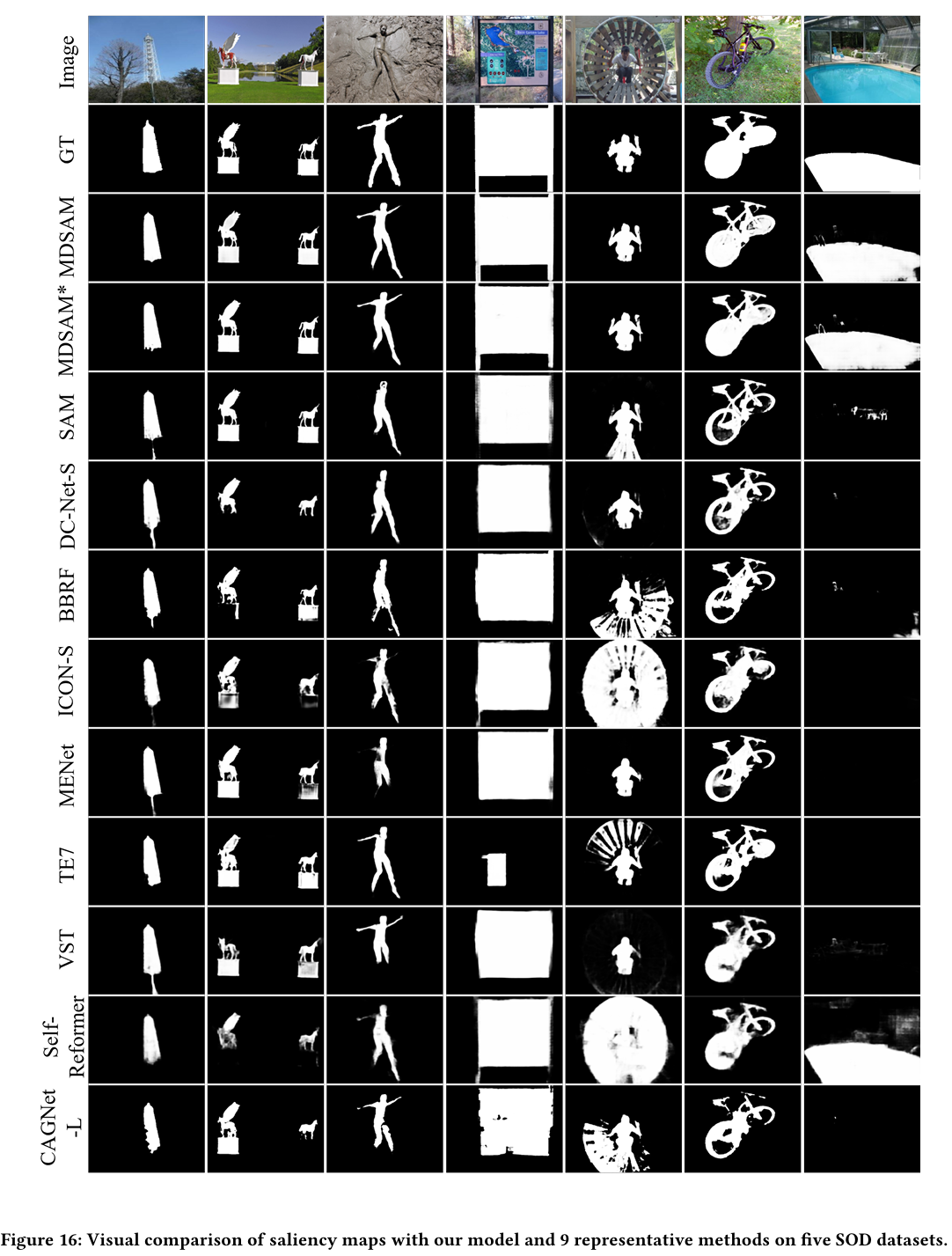
定性评估。图6展示了我们MDSAM与其他方法预测的显著图。在繁琐场景中，我们的MDSAM行准确定位各种大小的显著目标，并完全识别这些目标的形状。此外，我们提出的MDSAM的结果比其他方法显现更多细粒度细节和准确边缘。更多视觉示例允许在附录中找到。

4.3 消融研究

为了验证大家提出模块的有效性，我们在本节中进行消融研究。如果未指定，所有结果都是在512×512图像分辨率下获得的。

LMSA的有效性。为了验证LMSA的效果，大家只改变SAM的图像编码器。除了完全微调（FT）之外，我们将适配器[18]和LoRA[19]引入图像编码器，将SAM适应到SOD。此外，我们保持适配器、LoRA的参数与我们的LMSA相似，以进行公平比较。如表3所示，引入参数高效微调许可显著减少可训练参数并提高性能。此外，我们的LMSA与适配器和LoRA具有相似的参数。然而，它比它们表现出更好的结果。图8中的视觉比较进一步说明，LMSA的利用使模型能够获取多尺度信息。因此，它可以在复杂场景中准确定位不同大小和数量的显著目标。

MLFM的有效性。表4显示了MLFM的效果。第1-3行的结果表明，当我们采用级联作为融合方法时，性能提升是边缘的。主要原因是不充分的融合可能会向特征引入额外的噪声信息，从而限制性能提升。然而，当我们使用MLFM时，与没有融合策略相比有显著改进。如图7所示，简单的级联融合策略可能会混淆模型，导致错误预测。相比之下，使用我们提出的MLFM，模型可以更好地识别整个目标的形状和轮廓。这清楚地表明，我们提出的MLFM确保了SAM编码器多级信息的充分利用。

DEM的有效性。表4的第4-5行呈现了带有DEM及其MEEM组件的定量结果。许可看出，没有MEEM的DEM使用导致性能略有提升。然而，模型仍然缺乏足够的细节信息。此外，当整合MEEM时，模型性能显著提升。这些结果表明，MEEM的启用使模型能够捕获更多细节信息。图7证实，带有包含MEEM的DEM，模型获得了更多细粒度细节和边缘，达成了更好的SOD预测。

5 结论

在本文中，大家提出了一种名为MDSAM的新特征学习框架，用于SOD任务。该框架保留了SAM的预训练权重，同时整合了多尺度和细粒度信息。具体来说，通过在SAM编码器中引入LMSA，我们将SAM适应到SOD并使模型学习多尺度信息。此外，我们提出了MLFM，有效融合SAM编码器不同层的输出特征。为了增强SOD性能，我们提出了DEM来应对SAM中缺乏细粒度细节的问题。实验结果验证了我们方法的有效性和强大泛化能力。

致谢

本工作部分得到了中国国家自然科学基金（No. 62101092）和中央高校基本科研业务费专项资金（No. DUT23YG232）的支持。

参考文献

[1] Jimmy Lei Ba, Jamie Ryan Kiros, and Geoffrey E Hinton. 2016. Layer normalization. arXiv preprint arXiv:1607.06450 (2016).

[2] Jorge Bernal, Javier Sánchez, and Fernando Vilarino. 2012. Towards automatic polyp detection with a polyp appearance model. Pattern Recognition 45, 9 (2012), 3166-3182.

…

（注：由于篇幅限制，这里只展示了部分参考文献。完整的参考文献列表应包含原文中的全部引用。）

附录

A.1 模型泛化

原始SAM表现出强大的泛化能力。大家的MDSAM不仅向SAM引入了多尺度和细粒度细节，还保留了泛化能力。为了验证这一点，我们在伪装目标检测和息肉分割上进行了实验，这些任务具有很不同的域特征。

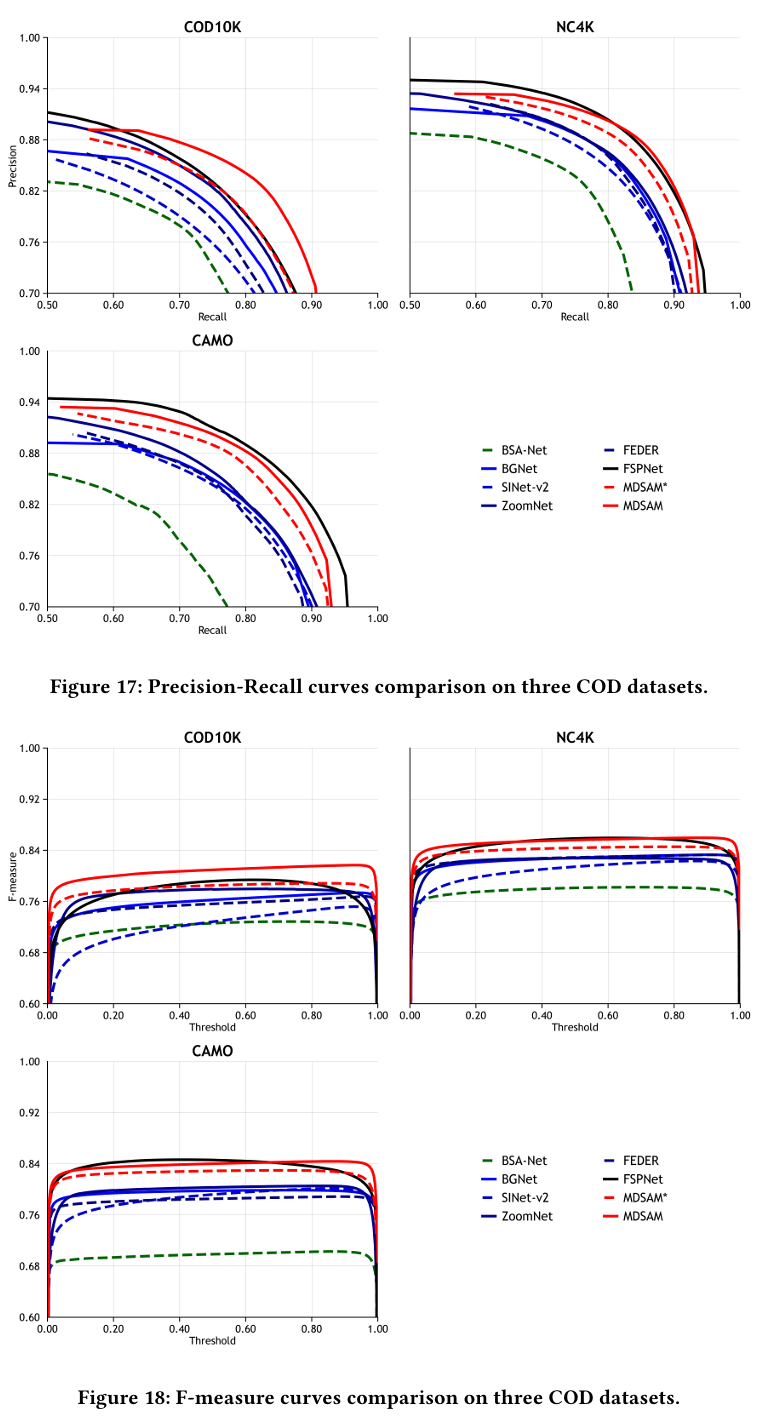
伪装目标检测（COD）：与旨在寻找显著目标的SOD不同，COD专注于在困难场景中检测伪装目标。在这里，我们采用三个COD数据集进行模型训练和测试。COD10K[11]包含5,066个伪装、1,934个非伪装、3000个背景图像。CAMO[24]包含1,250个伪装和1,250个非伪装图像。NC4K[34]包含4,121个伪装图像。我们采用与[20]相似的训练策略。我们在COD10K训练数据集和CAMO训练数据集中所有包含伪装目标的图像上训练我们的MDSAM。接着，我们在所有测试数据集上测试MDSAM。我们的MDSAM与三个SOD模型（即F3Net[54]、MINet[39]和VST[31]）和八个COD模型（即MGL-R[65]、C2FNet[45]、SINet-v2[11]、BSA-Net[76]、BGNet[46]、ZoomNet[38]、FEDER[14]和FSPNet[20]）进行比较。我们采用四个指标进行评估。与SOD不同，我们用平均F-measure$(F_{\beta }^m)$替换了最大F-measure$(F_{\beta }^{max})$。如表5所示，大家的MDSAM在COD任务上取得了相当的性能。在定性评估中，如图9所示，我们的MDSAM展示了更精确定位和细粒度细节。

息肉分割：我们进一步在息肉分割上进行实验，这是一种典型的医学图像分割任务。我们采用与Poly-PVT[7]相同的训练策略，并在Kvasir[21]、CVC-300[2]上测试我们的技巧。如表6所示，我们的方法在息肉分割上取得了卓越性能。此外，与使用适配器增强的SAM相比，我们的方法在COD和息肉分割上都要好得多。

通过从上述实验中，能够看出大家的MDSAM不仅在SOD任务上表现出色，而且在COD和息肉分割上也表现出卓越性能。它们清楚地展示了我们模型的卓越泛化能力。

A.2 零样本分析

SAM在给予提示时具有强大的分割能力。我们从真实标签中的每个连接组件提取边界框，并将其用作SAM的框提示。我们还应用SAM-HQ[22]进行实验，它使SAM能够分割高质量结果。如表7所示，当给出准确提示时，SAM在SOD上表现显著良好。然而，SOD需要相应的语义信息。当没有给出提示时，SAM表现不佳。我们的MDSAM不仅改进了SAM的分割，还学习了SOD的语义信息。

A.3 更多消融研究

在我们提出的LMSA中，我们应用平均池化（AP）获取多尺度特征。此外，我们引入局部细节信息来消除SAM的缺点。在本节中，我们在不同尺度的LMSA和MDSAM中是否引入局部信息进行实验。实验在完全设计的MDSAM下进行，模型的输入分辨率设置为512×512。

通过尺度效果。表8显示了运用不同池化尺度的效果。如方式(a)和(b)以及(d)和(e)所示，只要保持多尺度，尺度的变化对结果的影响极其小。然而，如途径©和(e)所示，多尺度方法通常比单尺度方法表现更好。图10展示了与单尺度设置©相比，多尺度设置(d)和(e)能够更准确地检测复杂场景中的显著目标。因此，LMSA的尺度设置倾向于保持多尺度。

局部信息的有效性。为了进一步探索局部信息的效果，我们进行了更多实验，如表8所示。行观察到，随着局部信息的引入，模型性能显著提升。此外，与方法(b)和方法(e)相比，许可看到我们的MDSAM在相同尺度下在存在局部信息时表现出更好的性能。图10说明，局部信息使模型能够提取更精确的特征，从而产生更好的显著图。

A.4 基于属性的分析

在本节中，我们通过在具有挑战性的SOC[12]信息集上评估我们提出的方法，提供基于属性的分析。SOC测试数据集分为9个主要类别，分别是外观变化（AC，79张图像）、大目标（BO，24张图像）、杂乱（CL，92张图像）、异质目标（HO，153张图像）、运动模糊（MB，32张图像）、遮挡（OC，157张图像）、视野外（OV，155张图像）、形状复杂性（SC，116张图像）和小目标（SO，389张图像）。我们将我们的MDSAM与17种方法进行比较，包括Amulet[70]、DSS[17]、NLDF[33]、SRM[49]、BMPM[66]、C2SNet[27]、DGRL[50]、RANet[3]、CPD[56]、EGNet[73]、PoolNet[30]、SCRN[57]、BANet[44]、MINet[39]、ICON-R[78]、DC-Net-R[77]和完全微调的SAM[23]。如表9所示，我们的MDSAM在512×512和384×384分辨率下在大多数场景中表现出卓越性能。并且它们在AC和BO类别上平均表现，这些类别数据量较少。图11显示了我们提出的MDSAM与六个代表性最先进方法的一些可视化结果。这种可视化表明，当前途径在准确定位大目标和小目标方面存在困难，结果缺乏细粒度细节。我们的MDSAM许可准确定位多尺度目标，边缘和细节都非常精确。

A.5 更多比较结果

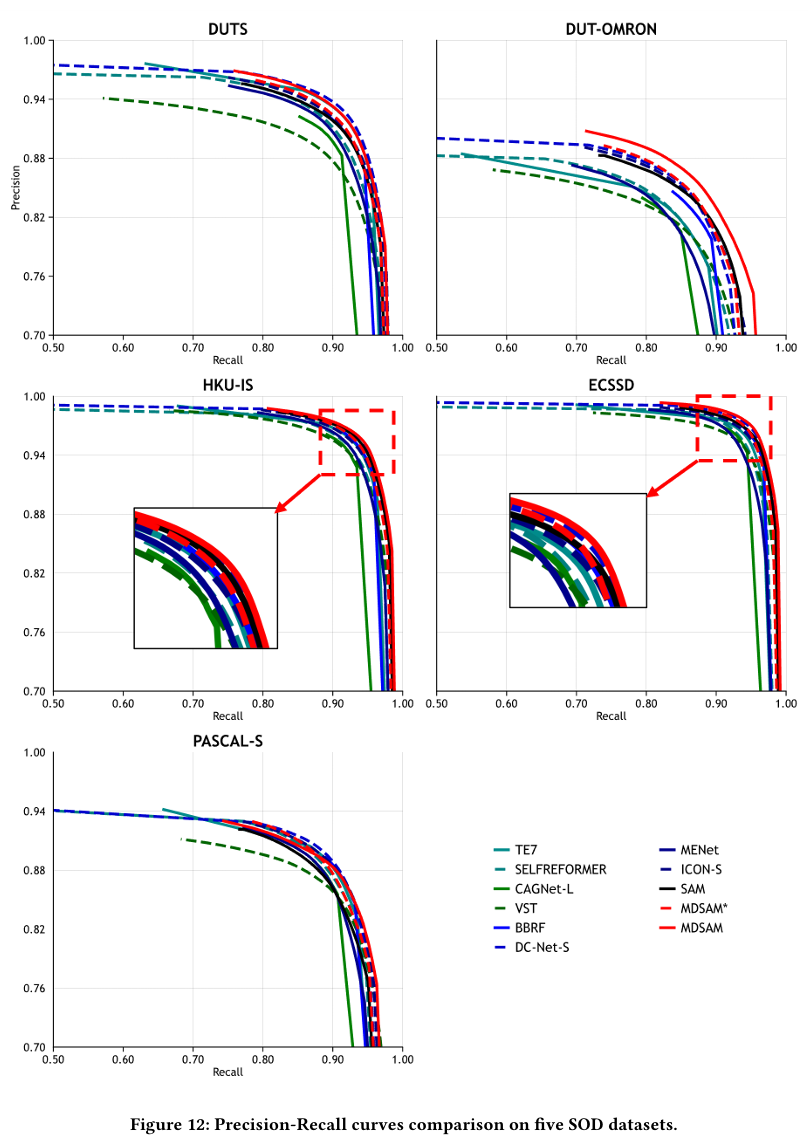
在主论文中，我们通过四个广泛应用的指标将我们的MDSAM与其他方式进行比较。在本节中，我们在五个SOD数据集上与CAGNet-L[37]、TE7[25]、MENet[52]、VST[31]、SelfReformer[63]、ICON-S[78]、BBRF[36]、DC-Net-S[77]和完全微调的SAM[23]比较，展示精确率-召回率曲线和F-measure曲线，分别如图12和图13所示。此外，我们在图14、图15和图16中给出了更多视觉比较。在图17和图18中，我们展示了在三个COD数据集上与SINet-v2[11]、BSA-Net[76]、BGNet[46]、ZoomNet[38]、FEDER[14]和FSPNet[20]比较的曲线。更多视觉比较表明在图19中。