深入解析：【C++升华篇】学习C++就看这篇---＞红黑树深度剖析

个人主页：HABuo

个人专栏：《C++系列》《Linux系列》《数据结构》《C语言系列》《Python系列》《YOLO系列》

⛰️ 如果再也不能见到你，祝你早安，午安，晚安

前言：
前面我们了解了二叉搜索树、AVLTree，其中AVLTree就是解决二叉搜索树插入数据有序的情况下，效率退化成O(N)的问题，AVLTree很巧妙了解决了上述问题，今天我们来了解另外的一个数据结构红黑树，红黑树也可以解决上述问题。事实上，实际使用中红黑树的应用会比AVLTree更广，所以希望大家以更加重视的态度来学习。

如果听了上面的话你不知道在讲什么，请一定先阅读这两篇文章:

【C++升华篇】学习C++就看这篇---＞二叉搜索树深度剖析

【C++升华篇】学习C++就看这篇---＞AVLtree深度剖析&模拟实现

本篇重点：
本篇文章着重讲解红黑树的概念以及性质，以及为了维护红黑树这种性质而做的限制条件，最后模拟实现红黑树的插入，带大家熟悉红黑树的变色和旋转规则!

一、红黑树的概念以及特性

什么是红黑树？

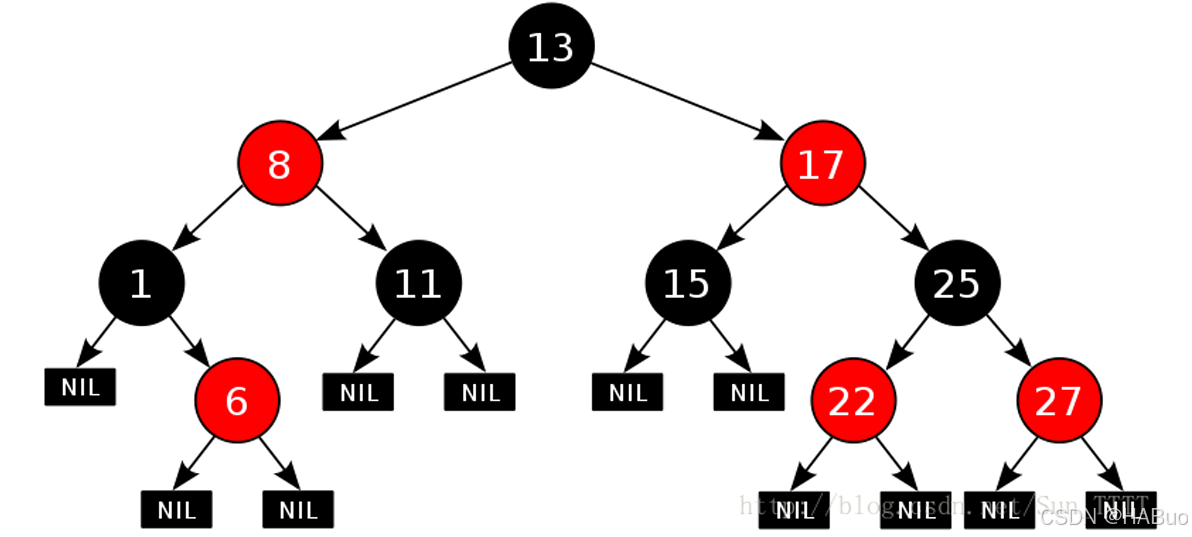
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

①红黑树是一颗二叉搜索树。

②每个节点都有颜色,红色或黑色

③最长路径最多是最短路径的二倍

为什么需要红黑树？

红黑树就是一种“自平衡”的二叉搜索树。 它的核心使命就是：通过在插入和删除操作时遵循一些特定的规则，来避免树退化成链表，从而保证最坏情况下操作时间也是O(log n)。（和AVLTree的使命是一样的）

红黑树的五项基本原则

①每个节点要么是红色，要么是黑色

②根节点永远是黑色的

③所有叶子节点（NIL节点）都是黑色的。

注意：在红黑树的定义中，叶子节点是指那些不存储数据的、空的（NIL）节点。通常我们在实现时，会用一个通用的、黑色的哨兵节点来代表所有NIL节点，这样可以节省空间并简化代码。

④红色节点的两个子节点都必须是黑色的。

核心规则！ 这意味着不能有两个连续的红色节点。红色节点不能和它的父节点同时为红色。

⑤从任意一个节点到其所有后代叶子节点的简单路径上，均包含相同数量的黑色节点。

这个数量被称为 “黑高”。这条规则保证了树的大致平衡，因为最长路径（红黑交替）也不会超过最短路径（全黑）的两倍。

二、红黑树的模拟实现

1.红黑树的基本结构

首先,每个节点都要存一个颜色，这里我们使用枚举enum来实现，并且和AVL一样也是三叉链!

enum Colour
{
	RED,
	BLACK
};
// 这里我们默认按key/value结构实现
template
struct RBTreeNode
{
	pair _kv;//每个节点所要存储的值
	RBTreeNode* _left;//依然采用三叉链的结构，容易实现
	RBTreeNode* _right;
	RBTreeNode* _parent;
	Colour _col;
	RBTreeNode(const pair& kv)
		:_kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
	{}
};
template
struct RBTree
{
    typedef RBTreeNode Node;
private:
	Node* _root = nullptr;
};

2.红黑树的核心操作与底层原理

红黑树的所有魔法都发生在插入和删除操作中。因为这两个操作可能会破坏上面的五项规则。为了修复规则，我们有两种基本武器：变色和旋转。

旋转的原理与AVLTree没有什么区别，唯一区别就是这里不需要注意平衡因子，因此这里就不再赘述，有需要的请前往下面这篇博客进行了解：

【C++升华篇】学习C++就看这篇---＞AVLtree深度剖析&模拟实现

旋转的目的： 降低树的高度，为后续的变色和平衡创造条件。

变色：简单地改变节点的颜色（红变黑，黑变红），这是最直接的修复规则4和规则5的方法。事实上颜色就可以当作一个标记，它就是用来调节红黑树以保持平衡。欲知故事如何，请看下文：

3.红黑树的插入操作

和AVL树很相似，红黑树的插入也是分为两步走:

①按照二叉搜索树的规则插入值

②插入后根据颜色或高度做旋转或变色

因此插入新节点的操作和之前是一样的，直接拷贝:

    bool Insert(const pair& kv)
	{
        if (_root == nullptr)
		{
			_root = new Node(kv);
			_root->_col = BLACK;
			return true;
		}
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur){
			if (cur->_kv.first < kv.first){
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_kv.first > kv.first){
				parent = cur;
				cur = cur->_left;
			}
			else
	            return false;
		}
		cur = new Node(kv);
		cur->_col = RED;
		if (parent->_kv.first < kv.first)
			parent->_right = cur;
		else
			parent->_left = cur;
		cur->_parent = parent;

下面我们来进行分析它是如何通过变色和旋转来维持它的平衡的:

当我们插入一个新节点时，我们总是先把它染成红色。为什么？因为插入一个红色节点对规则5（黑高相同）的破坏性最小，它不会改变路径上的黑高。

插入后，我们检查是否破坏了规则。主要矛盾就是规则4：不能有连续的两个红色节点。

设新插入的节点为 Cur，其父节点为 P，祖父节点为 G，叔叔节点（P的兄弟）为 U。

红黑树的插入操作详解(一)

情况1：如果插入的节点的父亲是黑色节点，那么正是我们想看见的,不用管它了!

情况2：cur为红，p为红，g为黑，u存在且为红，很明显，这违反了规则四，有连续的红色节点，所以此时需要做处理了!

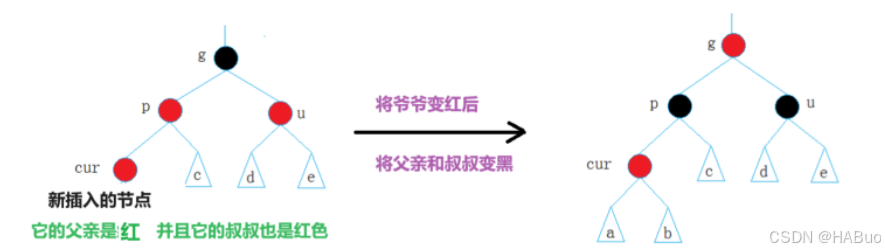通过这样的变化我们既保持了规则5，又让连续的红节点断开了，但是这里有几种情况：

①如果g是根节点，需要把它的颜色变回黑色

②如果g的父亲是黑色节点则更新结束

③如果g的父亲是红色节点则需要继续向上更新

情况3：cur为红，p为红，g为黑, u不存在/u为黑。这里的操作是既需要旋转有需要变色

①如果u不存在很明显cur就是新增节点

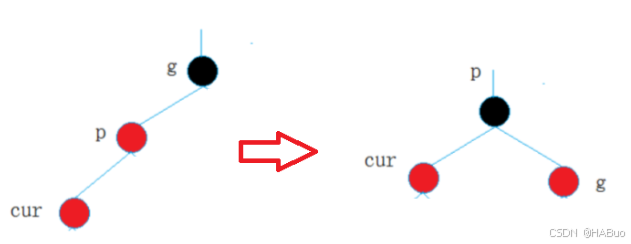
聪明的你一定会想到AVLTree中的旋转，因为很明显左边重，需要右单旋，右单旋之后，身为黑节点g跑到了右子树上，你们规则5就破坏了，因此我们需要将p节点和g节点的颜色进行互换。所以cur为红，p为红，g为黑, u不存在的情况，操作方法：右单旋 + p变黑g变红

②如果u存在且为黑

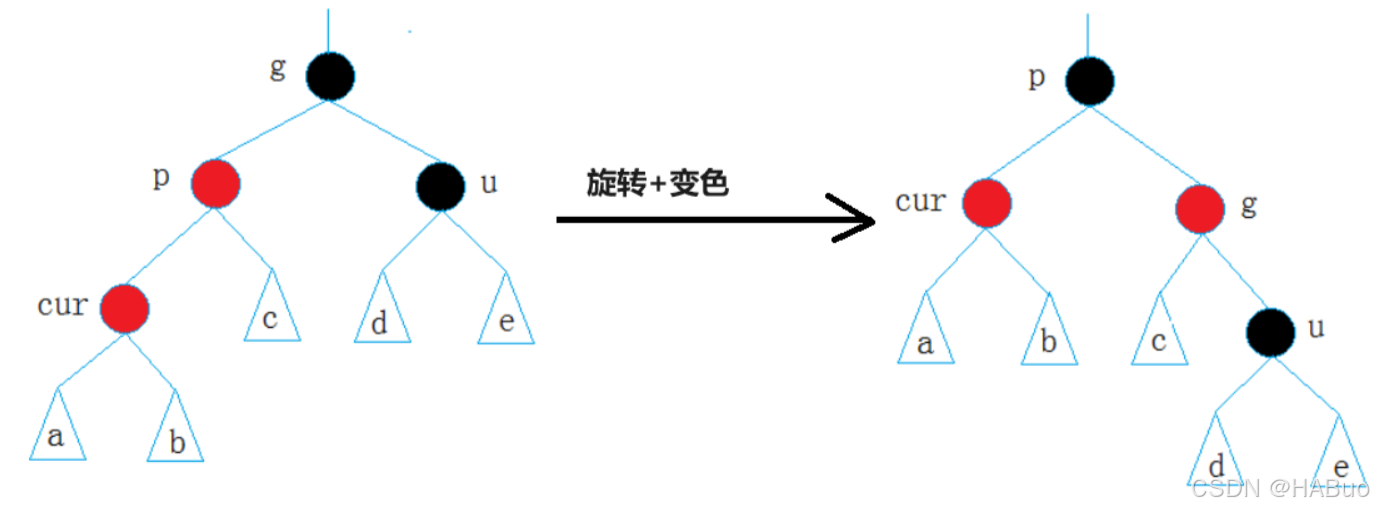
这里需要注意的是cur此时一定不是刚插入的节点，一定是上面情况2变换上来的，此时和u不存在的处理情况一致，先进行右单旋，再将p变为黑，g变为红

情况4：cur为红，p为红，g为黑, u不存在/u为黑（但cur是p右，出现了折线情况）。

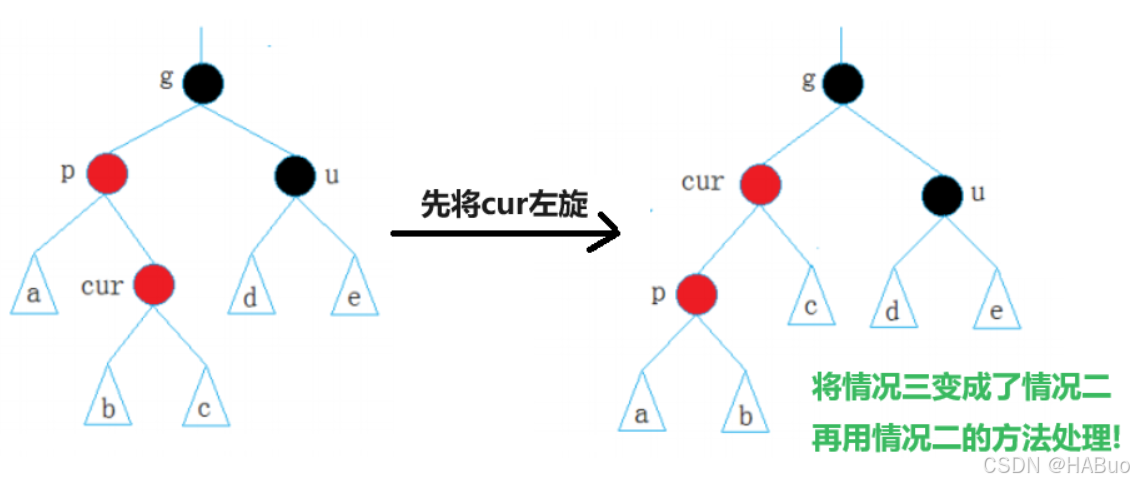
相信大家了解到这就是AVLTree中的双旋情况，我们先对p进行左单旋，再对g进行右单旋，不过要注意的是此时cur是情况3中②的p，再进行变色即可。

3.红黑树插入代码实现

在整个大情况分类中,可以归为两类一是叔叔为红色,二是叔叔为黑色或者叔叔不存在,我们围绕着这两个大方向写!

    while (parent && parent->_col == RED)
		{
			Node* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				Node* uncle = grandfather->_right;
				// 叔叔存在且为红->变色
				if (uncle && uncle->_col == RED)
				{
					parent->_col = BLACK;
					uncle->_col = BLACK;
					grandfather->_col = RED;
					// 继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else  // 叔叔不存在，或者叔叔存在且为黑->旋转+变色
				{
					if (cur == parent->_left){
						//     g
						//  p    u
						//c
						// 右单旋
						RotateR(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else{
						//     g
						//  p     u
						//    c
						// 左右单旋
						RotateL(parent);
						RotateR(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
			else // grandfather->_right == parent
			{
				//   g
				// u   p
				Node* uncle = grandfather->_left;
				// 叔叔存在且为红，-》变色即可
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLACK;
					grandfather->_col = RED;
					// 继续往上处理
					cur = grandfather;
					parent = cur->_parent;
				}
				else // 叔叔不存在，或者存在且为黑
				{
					// 情况二：叔叔不存在或者存在且为黑
					// 旋转+变色
					//   g
					// u   p
					//       c
					if (cur == parent->_right)
					{
						RotateL(grandfather);
						parent->_col = BLACK;
						grandfather->_col = RED;
					}
					else
					{	//    g
						// u     p
						//     c
						RotateR(parent);
						RotateL(grandfather);
						cur->_col = BLACK;
						grandfather->_col = RED;
					}
					break;
				}
			}
		}
		_root->_col = BLACK;
		return true;

解释：可以发现一个问题，只要是叔叔的颜色是黑色或叔叔不存在的情况下,执行完旋转＋变色后都直接break了，这是因为在这种情况下,父亲节点都被变成了黑色，也就没必要继续往上了!并且在红黑树的左旋和右旋中,代码其实和AVL树的旋转是一模一样的，所以直接copy一份就行了!我们分析的都是插入节点在根节点的左子树上，事实上，在右子树上道理是一样的，大家仔细的分析即可明白，在这里就不再赘述。

三、总结

①理解规则： 五项规则是红黑树的灵魂，务必记牢。

②掌握工具： 旋转和变色是修复规则的唯一手段。

③分情况讨论： 插入和删除的逻辑都是通过严谨的情况分析来处理的。画图！自己动手画一画每种情况的演变过程，这是理解它们最好的方式。

④实际应用： 在C++的STL中，std::map和std::set的底层通常就是红黑树。

拓展阅读：

红黑树的删除图解

AVLTree与红黑树的对比
增删查改时间复杂度是：O(LogN）
最短路径是：O(LogN)
最长路径是：2*O(LogN)
也就是说理论上而言，红黑树的效率比AVL树略差，但是现在呢，硬件的运算速度非常快，他们之间己经基本没有差异了。因为常规数据集中logN足够小，2*logN差异不大。
为什么AVLTree和红黑树性能基本差了2倍，但是我们认为基本是一样的呢？因为硬件足够快，比如10亿个数查找AVLTree最多查找30次。红黑树最多查找60次。30和60最现在的硬件基本是一样的。但是插入删除同样节点红黑树比AVL树旋转更少，因为AVLTree更严格的平衡其实是通过多旋转达到的，所以实际红黑树得到了更广泛的应用。其次红黑树实现上更容易控制。

posted @ 2025-12-02 11:52 yangykaifa 阅读(10) 评论(0) 收藏举报

刷新页面返回顶部