算法沉淀第十一天（序列异或） - 详解

目录

引言：

序列异或

题意分析​编辑

        逻辑梳理

        代码实现

        AC码

        代码讲解

结语：

---

引言：

时隔多日，我又来沉淀算法了，今天我们来讲一下我的训练题，这道题在没有我学长的讲解帮助下，我还真完全想不到有这么新颖的解法，太通透了

那么，话不多说，大家就进入今天的算法讲解———————>

---

序列异或

按照惯例，大家先来看题目

        题意分析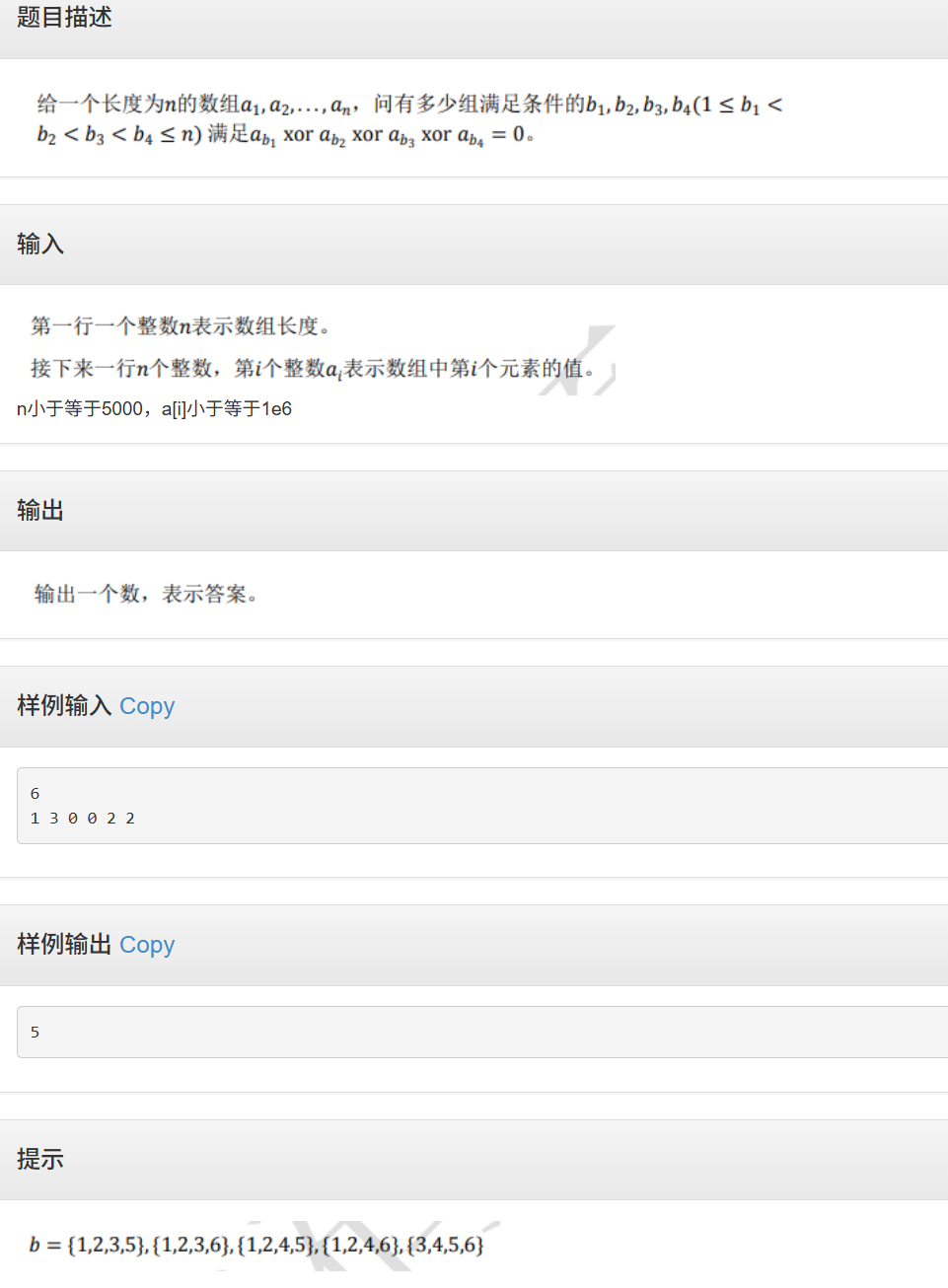

这个题就是给你一个数组，然后四个不同下标的数为一组，如果一组数异或下来的结果是0，那么这个数就是符合条件的，问你有几组符合条件的数，输出即可

那么，题目分析完了，我们进入逻辑梳理环节

---

        逻辑梳理

这题的内容范围给的很低，然而如果通过四层循环来找毋庸置疑会超时，这个时候我们可以通过异或的性质（a^a=0），将一组4个元素的数拆成2组2个元素的数，只要这俩组数异或的结果一样的话，那么就找到一组数了

通过那么，我们能够通过循环来找2个为一组的材料，那么 ，我们能够用一个数组来统计异或结果为x时候的组数有几组，将这个几放在下标为x的位置

在第三个下标和第四个下标为固定时候满足的组数的数量，然后更新结果，然后再从开始位置到当前第三个下标位置的所有元素分别和当前第三个下标的元素进行异或的结果作为下标的数组元素值++，源于下一次循环时候，第三个下标位置就变成了之前第三个下标位置的下一位就是上面那个数组是预处理到第三个下标前的数，然后再通过第三个下标和第四个下标异或的结果的下标上的该数组的元素就

直接讲的话会很抽象，因为我也是第一次接触这种高级更新优化法，那么，我们借助代码来讲解

---

        代码实现

AC码很短，但是思路特别巧妙，这里先放AC码，如下

        AC码

#define _CRT_SECURE_NO_WARNINGS
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
int a[5010];
long long t[2000010];
void solve()
{
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++)
	{
		cin >> a[i];
	}
	long long ans = 0;
	for (int i = 1; i <= n; i++)
	{
		for (int j = i + 1; j <= n; j++)
		{
			ans += t[a[i] ^ a[j]];
		}
		for (int j = 1; j < i; j++)
		{
			t[a[i] ^ a[j]]++;
		}
	}
	cout << ans << endl;
	return;
}
int main()
{
	solve();
	return 0;
}

---

        代码讲解

那么，我们依据上面的代码来讲讲具体达成方式，

开始，ｔ这个数组表示的就是组数，ｉ下标的元素表示异或结果是ｉ的组数（这个组数指的是２个一组的组数）

然后，ｉ表示的是第三个下标，然后大家先不看第一个for循环，我们看下面那个for循环，那个for循环是从数组的第一个元素开始，然后到第三个下标之前，这是在算第一个下标和第二个下标做的组，第一个下标是就是那个循环，第二个下标就是现在循环的i，源于这边循环迭代完再++后，第三个下标就到后面的一位去了。

那么，接下来我们来看第一个for循环 ，第一个for循环就是在更新ans的值了，ans的值就是答案，在第一个for循环里的就是第三个下标和第四个下标，然后第三个下标和第四个下标异或得到的值跟先前能异或出这个值的组相异或就可能得到0，故而只要求加上先前能异或出这个值的组的数量就可以了，也就是下标为这个值得ｔ的元素

那么，为什么第一个循环放在第二个循环前面呢，因为第二个循环执行时候相当于ｉ该位置的下标已经是作为第二个下标来进行更新了，所以要放在第一个循环后面

那么，这道题的大体代码分析就是该样子

---

结语：

今日算法讲解到此结束啦，希望对你们有所帮助，谢谢观看，如果觉得不错可以分享给朋友哟。有什么看不懂的可以评论问哦，