完整教程:机器学习核心概念四->逻辑回归与梯度下降实现
线性回归用于预测一个数值,而分类中大家输出变量y只能取少数几个可能值中的一个,而不是无限范围内的任意数值。线性回归并不是分类问题的好方法,接下来我们学习逻辑回归。
什么是决策边界?
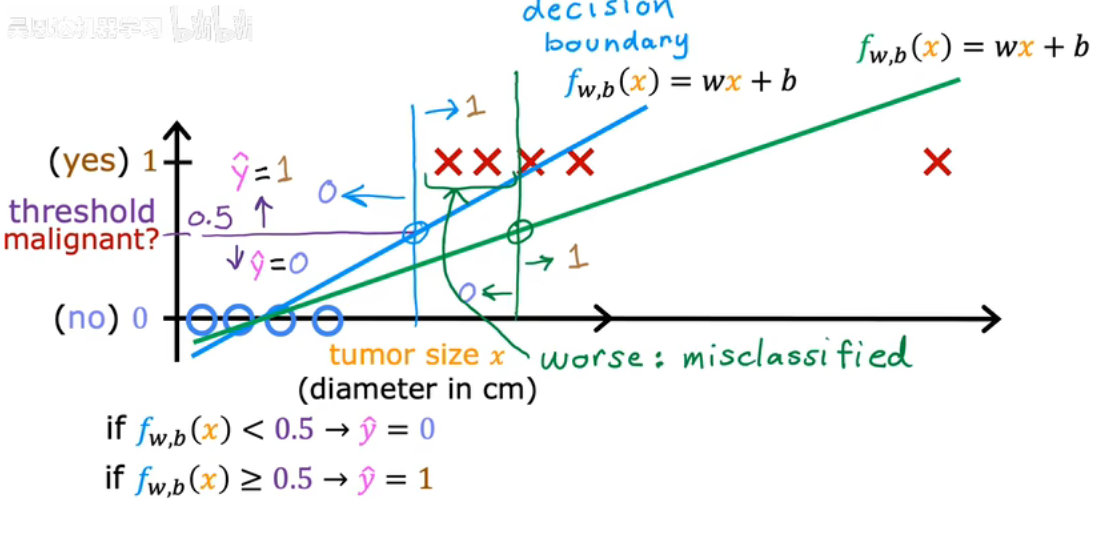
将不同类别分割开来的界限或曲面就是在分类问题中,“决策边界”
- 对于二分类问题:决策边界是把预测为类别0和类别1的区域分开的边界
- 实质上,决策边界是模型输出概率为0.5的点集
- 可以理解为逻辑回归在特征空间里画的一条“界限”,把两类信息尽量分开
逻辑回归
sigmoid function
为了建立逻辑回归算法,先介绍一个重要的数学函数-sigmoid function(logistic function)
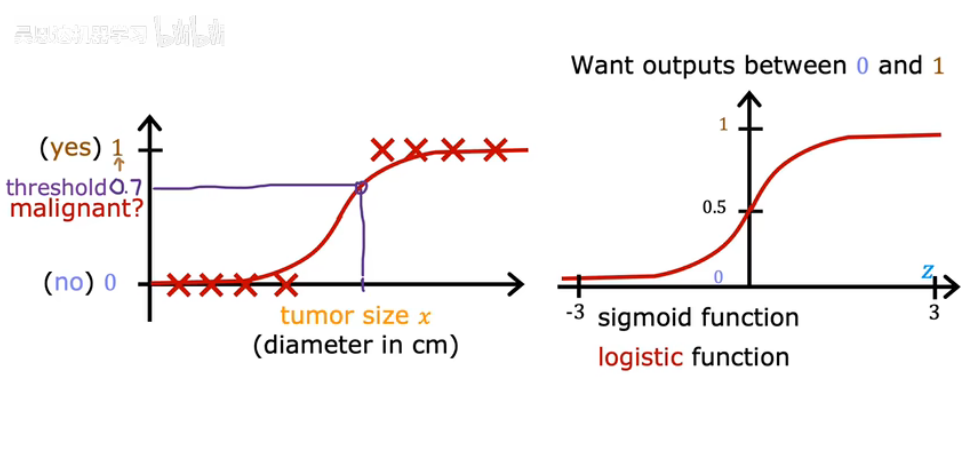
- 公式:
- 平滑连续,可导->方便梯度下降优化
- 输出
总是介于0和1之间,许可被理解为概率值
逻辑回归模型
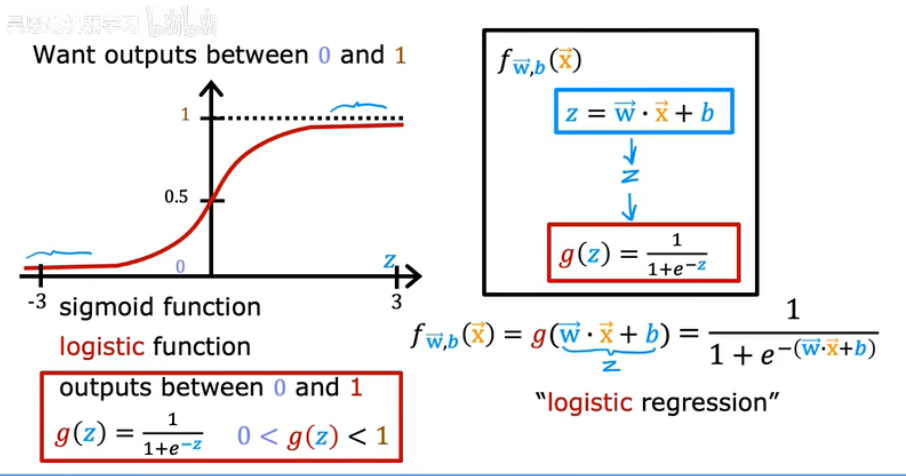
逻辑回归并不是“回归”,而是一种二分类模型
- 线性组合输入特征:
- 映射到概率:
p表示样本属于“”正类‘的概率’,负类概率就是1-p
- 预测类别:
为什么要用sigmoid函数?
- 输出概率:大家希望模型输出0-1的概率值,sigmoid函数把实数压缩到0-1能够直接表示概率
- 可导,方便优化:逻辑回归用最大似然估计(MLE)来训练模型;MLE要求对损失函数求梯度;sigmoid可导,方便用梯度下降优化参数
- 与概率逻辑一致:sigmoid函数对应logistic分布的积累分布函数;它满足概率模型对数几率(log-odds)线性关系的假设
总结流程:
- 初始化参数w,b:随机给一组小数(起点),是训练开始的前提
- 计算预测概率:对每个样本
计算线性组合
,通过sigmoid映射得到概率
- 计算损失(负对数似然/NLL):用训练数据的真实的标签
来衡量模型概率预测的好坏:
- 梯度下降更新参数:根据损失函数对w,b求梯度;更新参数w;重复迭代知道损失收敛
- 训练完成:得到最有参数,模型输出概率
- 训练阶段=不断预测概率+计算损失+调整参数;预测阶段:用训练好的参数输出概率->转换为类别
核心思想模型输出概率解释合理,同时便于梯度优化就是:用sigmoid把线性预测值转化成为概率,
决策边界
学习逻辑回归模型后,我们来看看决策边界,更好的理解逻辑回归是如何计算其预测值的。
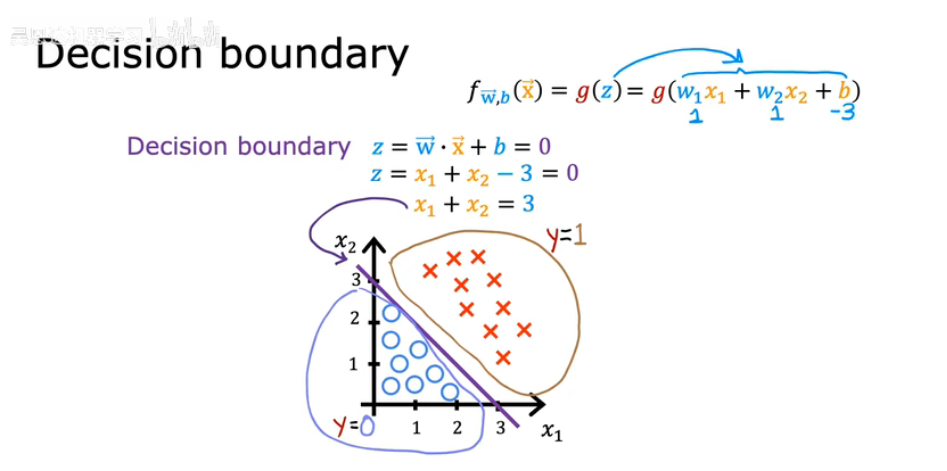

可以经过更高级的多项式得到更复杂的决策边界
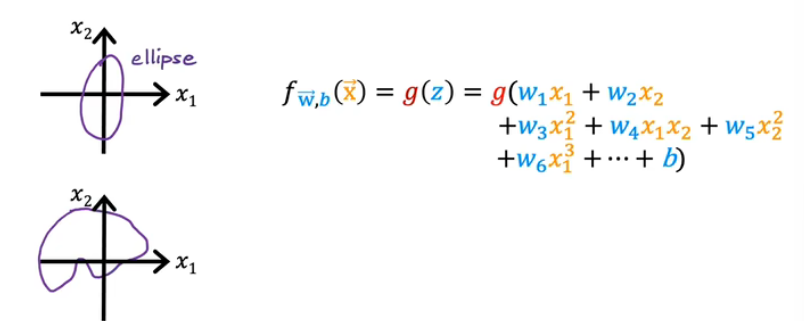
决策边界的概念
- 定义:决策边界是模型区分不同类别的分界线或超平面
- 在逻辑回归中,预测类别0或1的阈值一般为0.5使预测概率p=0.5的点的集合就是,决策边界就
- 这里
是线性组合,决策边界是线性方程:二维特征
是直线;三维特征是平面;更高维度是超平面
决策边界的作用
- 分类作用:把特征空间分成两部分:一边预测0,一边预测1
- 可视化理解:可以滑出数据点和分界线,直观展示模型效果
- 优化目标:训练时通过调整w,b移动决策边界,使得训练样本被正确分开
- 逻辑回归的就是决策边界核心可视化工具,在高位空间虽然看不到,但是数学意义是一样的
逻辑回归的代价函数
成本函数为你提供了一种衡量特定参数集与训练数据适合度的方式,进而为你提供了一种选择更好参数的办法。接下来我们将讨论为什么平放误差成本函数不是逻辑回归的理想成本函数,并介绍一直可以帮助我们为逻辑回归选择更好参数的不同成本函数。
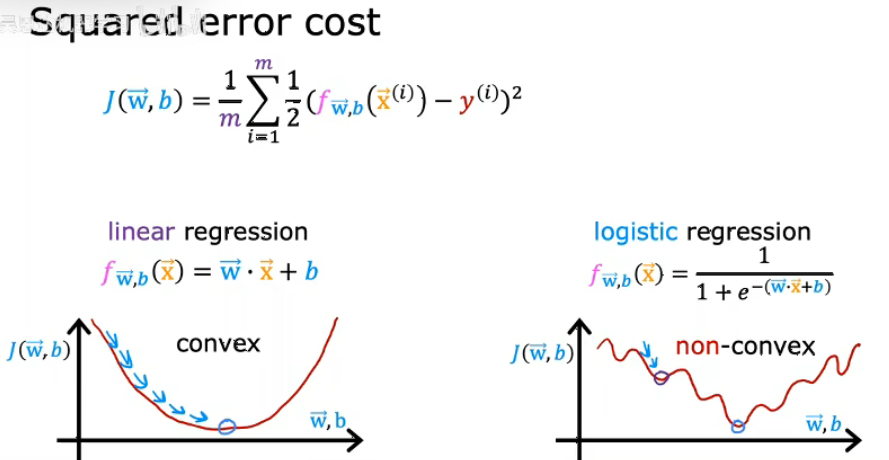
如上图所示,如果使用相同的成本函数来进行逻辑回归,并用这个f(x)值来绘制成本函数,成本函数会变成所谓的非凸成本函数,如果尝试使用梯度下降算法,将会在很多局部最小值中陷入困境,接下来介绍一种函数,它能够保证逻辑回归的成本函数是凸函数,这样梯度下降才能保证收敛到全局最小值。
用于逻辑回归的损失函数的定义如下
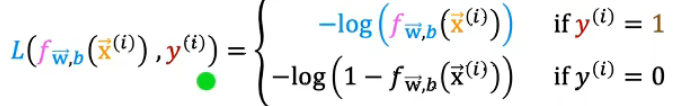
- 损失函数衡量的是单个训练样本的表现,通过对所有样本的损失求和,你可以得到代价函数,它衡量的是整个训练集的表现。
- f是逻辑回归的输出,因此f总在0到1之间,因为逻辑回归的输出实在0到1之间。所以函数的作用范围只有一部分 。
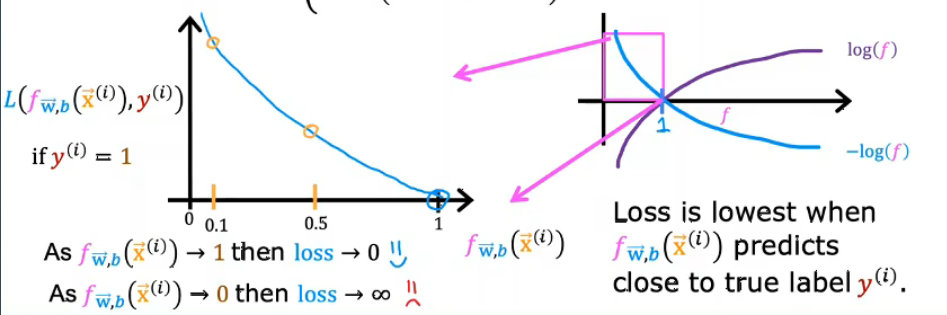
1.真实标签y=1:对于真实标签为1的样本,不同预测概率对应的损失变化
- 损失函数对应“上半部分”即分段函数y=1的部分
- 横轴是模型预测概率
,纵轴是对应的损失
- 当
-->1,损失-->0
- 当
-->0,损失-->
- 说如果模型预测就是也就
L=−log(0.5)就是=0.5,损失就
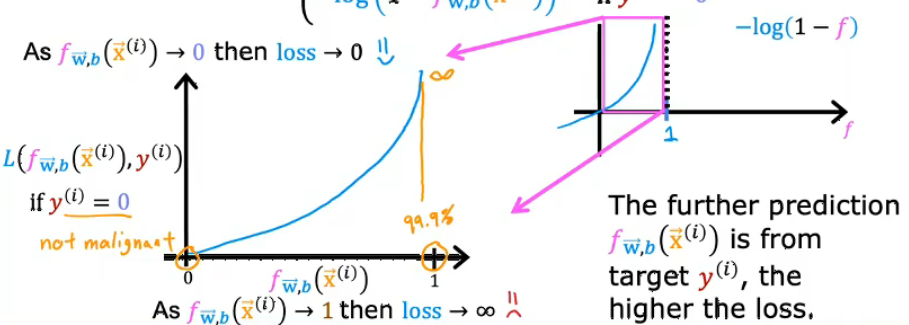
2.真实标签y=0 : 对于真实标签为0的样本,不同预测概率对应的损失变化
- 损失函数对应“下半部分”即分段函数y=0的部分
- 横轴是模型预测概率
- 当
-->1,损失-->
- 当
-->0,损失-->0
逻辑回归的简化版代价函数
接下来介绍一种稍微容易的手段写出损失函数和成本函数,这样当我们使用梯度下降来拟合逻辑回归模型的参数时会简单一些。


- 为了方便数学处理,我们把分段函数写成一个统一公式,这个公式同时包含了y=0和y=1的情况
- 统一写法后能够直接对
求导,用梯度下降更新参数
- 计算机搭建也更简单,可以直接向量化处理多个样本
- 之所以称为“简化版”,不是说损失函数本身更简单,而是把分段形式统一成一个公式,更方便计算和优化
| 方面 | 分段形式 | 简化版(统一公式) |
| 表达 | 根据y=0或y=1分段 | 用一个公式统一表达 |
| 数学处理 | 不方便求导 | 方便求导,向量化,梯度下降 |
| 本质 | 衡量单个样本预测好坏 | 等价于负对数似然,方便训练整个模型 |
| 优势 | 易于理解 | 方便实现和优化 |
简化版只是把分段函数统一成一个公式,本质没边。它和最大似然估计直接对应,训练逻辑回归就是在最小化负对数似然。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号