机器学习（3）梯度下降 - 指南

一、梯度下降（Gradient Descent）

1. 基本概念

梯度下降（Gradient Descent） 是一种用于 最小化代价函数 J(w,b)J(w,b)J(w,b)的优化算法。

它的思想相当直观：

环顾四周，选择让代价函数下降最快的方向，然后沿着该方向走一步。然后在新的位置重复这个过程，直到到达最低点。这种“下山”的过程，就是梯度下降。

2. 核心思想（Intuition）

假设你站在一座山上，天气太黑看不清地形。你只能摸索坡度最陡的方向（即梯度方向的反方向）一步步往下走。

• 每次往下走一步，就更新当前点的位置。

• 最终到达的山谷底部，就是代价函数的最小值。

这个最小点被称为：

局部最小值（Local Minimum）
凸函数（如线性回归中的碗状函数），那么局部最小值同时也是就是如果代价函数全局最小值（Global Minimum）。

3. 参数更新公式（Update Rule）

梯度下降通过不断调整参数 w 和 b，让代价函数 J(w,b) 逐步减小。

公式如下：

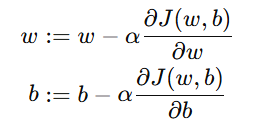
其中：

符号	含义
α	学习率（Learning Rate）
	对权重 w 的偏导数（梯度）
	对偏置 b 的偏导数
“:=”	表示赋值更新

补充： 同步更新的重要性

更新时，w 和 b 必须同时更新（Simultaneous Update）：

• 不应先更新 w 再用新的 w 去计算 b；

• 否则会导致不一致的结果，收敛路径混乱。

4. 梯度方向与代价变化

• 梯度（Gradient）表示函数上升最快的方向。

• 因此，大家沿着梯度的反方向更新参数，才能让代价下降。

数学上：

• 当梯度为正：说明函数在该点处上升 → 我们应减小 w

• 当梯度为负：说明函数在该点处下降 → 我们应增大 w

通过不断调整，J(w,b) 的值会持续减小，直到达到最小点。

5. 学习率 α\alphaα 的选择

学习率（Learning Rate）控制了每一步的前进速度。

学习率大小	效果	图示描述
太小	下降速度慢，训练时间长	缓慢接近最低点
太大	可能跨过最低点，甚至震荡发散	跳过碗底
合适	稳定快速收敛	顺滑下降到最小值

当代价函数到达最小点时：
梯度 =0，此时更新量为 0，w,b 不再变化。

示意图：

学习率太小 → 慢慢下降到谷底

学习率太大 → 直接跳过谷底、来回震荡

---

二、线性回归的梯度下降（Gradient Descent for Linear Regression）

1. 代价函数回顾

线性回归的代价函数定义为：

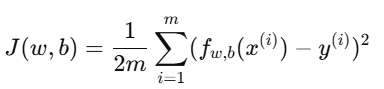
其中：

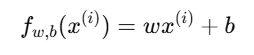
2.梯度公式推导

我们要求出代价函数对 w 和 b 的偏导数：

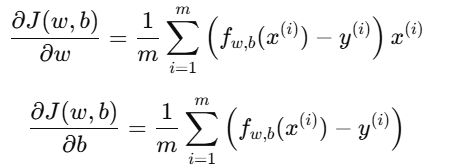
3.参数更新公式（线性回归专用）

将梯度代入更新规则：

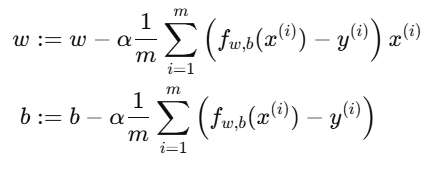
4.特点分析

• 代价函数是凸函数（Convex Function）

  • 形状像一个“碗”；

  • 没有多个局部最小值；

  • 因此梯度下降一定能收敛到全局最优解。

• 每次更新都让 J(w,b) 更小

  • 利用迭代逐步逼近最优参数。

5. 举例说明（Intuitive Example）

假设我们在训练一个简单的线性模型来预测房价：

x（房屋面积）	y（房价）
50	150
100	300
150	450

初始参数： w=0,b=0

每次迭代：

1. 根据当前 w,b 计算预测值；

2. 计算误差（预测 - 实际）；

3. 计算代价函数 J(w,b)；

4. 根据梯度更新 w,b。

经过若干次更新后，模型会逐步收敛到最佳拟合直线。

6.小结（Summary）

项目	内容
目标	最小化代价函数 J(w,b)J(w,b)J(w,b)
更新规则	w:=w−α∂J∂ww := w - \alpha \frac{\partial J}{\partial w}w:=w−α∂w∂J​，b:=b−α∂J∂bb := b - \alpha \frac{\partial J}{\partial b}b:=b−α∂b∂J​
学习率	控制更新步长
同步更新	w,bw,bw,b 同时更新
可视化	曲面下降、等高线收敛
线性回归的特性	代价函数为凸函数，仅有一个全局最小值