最优化？达成目标的最优方案2.最优化的发展3.最优化的特点计算机结合，适用范围广，联系实际4.生活中的最优化5.最优化数学模型6.最优化方法复杂性评价指标：时间空间复杂性，执行的次数，占用的存储空间7.最优化分类大致看一下，目标函数：线性、非线性。就是1.什么

一、概念

1.什么是最优化？

达成目标的最优方案

2.最优化的发展

3.最优化的特点

计算机结合，适用范围广，联系实际

4.生活中的最优化

5.最优化数学模型

目标函数

决策变量

约束条件

6.最优化方法复杂性

评价指标：时间空间复杂性，执行的次数，占用的存储空间

7.最优化分类

大致看一下，目标函数：线性、非线性

二、最优化数学基础

1.线性代数

（1）范数

范数概念

常用向量范数

向量的lp范数：

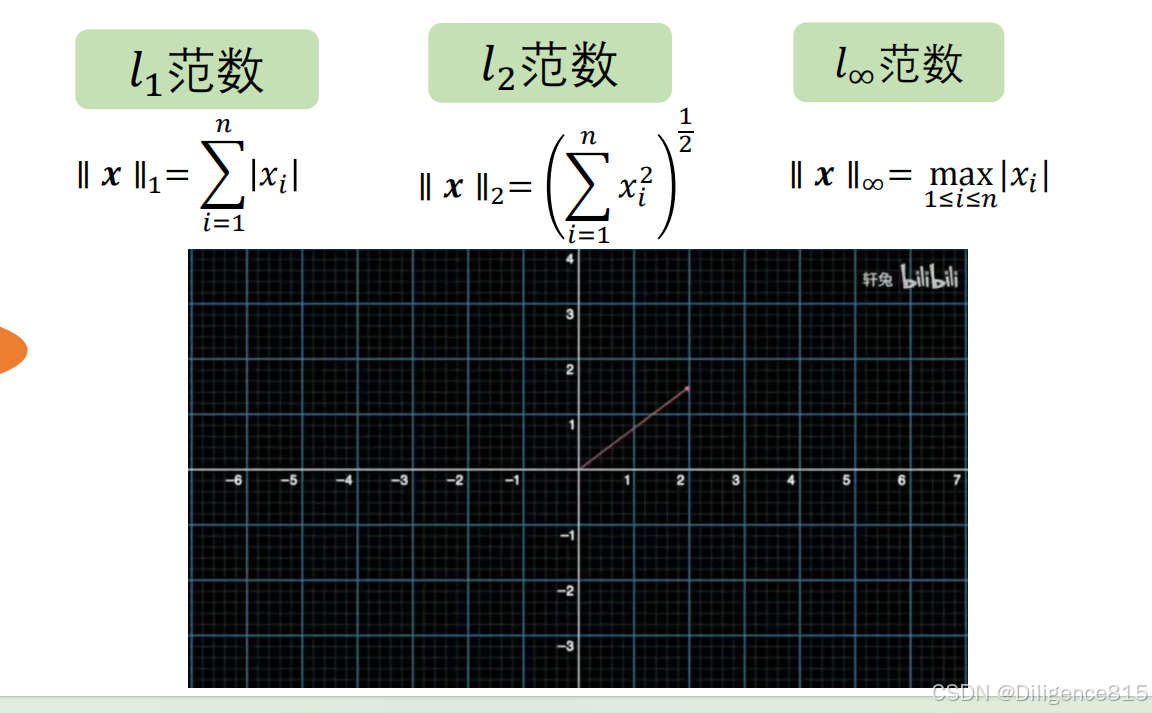
等价向量范数

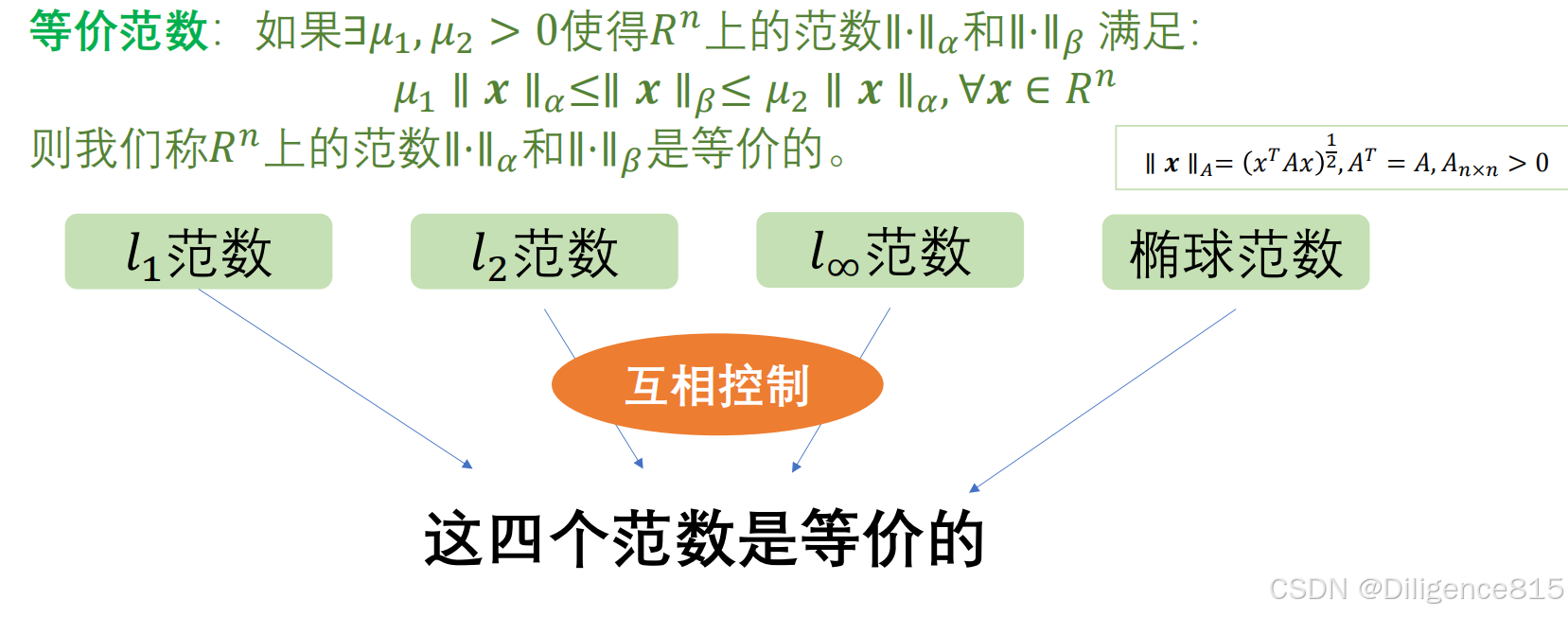
一范数和无穷范数的等价性。

向量范数不等式：不考

矩阵范数

（2）矩阵：看一下，小题

矩阵的阶

矩阵的转置T

矩阵的秩r

矩阵的迹Tr，主对角线元素之和，特征值之和

矩阵的逆

矩阵的行列式det

矩阵的特征值Ax=ax

2.微积分：梯度

连续

导数

可微可导

差商

3.凸分析：如何判断是否为凸函数？

凸集

凸函数

凸集的分离与支撑

三、特殊情形——Linear Programming,LP 线性规划

是最优化问题的特殊情形，实质是选出一组变量作为解，使得其满足一组确定的线性式（约束条件）条件下，让一个线性函数（目标函数）达到最优。

根据目标函数，可分为最大化问题与最小化问题；根据决策变量的线性表达式和常数项之间的连接符，可分为大于等于约束、等于约束、小于等于约束。

一般形式是什么？

其标准形表示形式如下：

$eq?min%20%5Cquad%20z%3Dc_%7B1%7Dx_%7B1%7D+c_%7B2%7Dx_%7B2%7D+%5Ccdot%20%5Ccdot%20%5Ccdot%20+c_%7Bn%7Dx_%7Bn%7D$ 目标函数要取得最小值

$eq?s.t.%5Cquad%20a_%7B11%7Dx_%7B1%7D+a_%7B12%7Dx_%7B2%7D+%5Ccdot%20%5Ccdot%20%5Ccdot+a_%7B1n%7Dx_%7Bn%7D%3Db_%7B1%7D%5C%5C$ 线性约束均为等式约束

$eq?%5Cquad%20%5Cquad%20a_%7B21%7Dx_%7B1%7D+a_%7B22%7Dx_%7B2%7D+%5Ccdot%20%5Ccdot%20%5Ccdot+a_%7B2n%7Dx_%7Bn%7D%3Db_%7B2%7D$

$eq?%5Ccdot%20%5Ccdot%20%5Ccdot%20%5Ccdot%20%5Ccdot%20%5Ccdot$

$eq?%5Cquad%20%5Cquad%20a_%7Bm1%7Dx_%7B1%7D+a_%7Bm2%7Dx_%7B2%7D+%5Ccdot%20%5Ccdot%20%5Ccdot+a_%7Bmn%7Dx_%7Bn%7D%3Db_%7Bm%7D$

$eq?x_%7B1%7D%5Cgeqslant%200%2Cx_%7B2%7D%5Cgeqslant%200%2C%5Ccdot%20%5Ccdot%20%5Ccdot%20%2Cx_%7Bn%7D%5Cgeqslant%200$ 所有决策变量都要满足非负约束

“等效”的，即转化后问题的最优解一定能通过某种方式推出原问题的最优解就是注意，这种转换必须

简化形式：

$eq?min%20%5Cquad%20%5Csum_%7Bj%3D1%7D%5E%7Bn%7Dc_%7Bj%7Dx_%7Bj%7D$

$eq?s.t.%5Cquad%20%5Csum_%7Bj%3D1%7D%5E%7Bn%7Da_%7Bij%7Dx_%7Bj%7D%3Db_%7Bi%7D%2Ci%3D1%2C2%2C...%2Cm$

$eq?x_%7Bj%7D%5Cgeqslant%200%2Cj%3D1%2C2%2C...%2Cn$

向量形式：

$eq?min%20%5Cquad%20z%3Dc%5E%7BT%7Dx$

$eq?s.t.%5Cquad%20%5Csum_%7Bj%3D1%7D%5E%7Bn%7Dp_%7Bj%7Dx_%7Bj%7D%3Db$

$eq?x_%7Bj%7D%5Cgeqslant%200%2Cj%3D1%2C2%2C...%2Cn$

$eq?c%3D%5Cbigl%28%5Cbegin%7Bsmallmatrix%7D%20c_%7B1%7D%5C%5Cc_%7B2%7D%20%5C%5C...%20%5C%5Cc_%7Bn%7D%20%5Cend%7Bsmallmatrix%7D%5Cbigr%29%5Cquad%20x%3D%5Cbigl%28%5Cbegin%7Bsmallmatrix%7D%20x_%7B1%7D%5C%5Cx_%7B2%7D%20%5C%5C...%20%5C%5Cx_%7Bn%7D%20%5Cend%7Bsmallmatrix%7D%5Cbigr%29%5Cquad%20p_%7Bj%7D%3D%5Cbigl%28%5Cbegin%7Bsmallmatrix%7D%20a_%7B1j%7D%5C%5Ca_%7B2j%7D%20%5C%5C...%20%5C%5Ca_%7Bmj%7D%20%5Cend%7Bsmallmatrix%7D%5Cbigr%29%5Cquad%20b%3D%5Cbigl%28%5Cbegin%7Bsmallmatrix%7D%20b_%7B1%7D%5C%5Cb_%7B2%7D%20%5C%5C...%20%5C%5Cb_%7Bm%7D%20%5Cend%7Bsmallmatrix%7D%5Cbigr%29$

矩阵形式：

$eq?min%20%5Cquad%20z%3Dc%5E%7BT%7Dx$

$eq?s.t.%20%5Cquad%20Ax%3Db$

$eq?x%5Cgeqslant%200$

$eq?A%3D%28p_%7B1%7D%2Cp_%7B2%7D%2C...%2Cp_%7Bn%7D%29%3D%5Cbegin%7Bbmatrix%7D%20a_%7B11%7D%20%26...%20%26a_%7B1n%7D%20%5C%5C%20...%26...%20%26%20...%5C%5C%20a_%7Bm1%7D%26...%20%26a_%7Bmn%7D%20%5Cend%7Bbmatrix%7D$

集合形式：

$eq?min_%7Bx%5Cepsilon%20D%7D%20%5Cquad%20z%3Dc%5E%7BT%7Dx$

$eq?D%3D%5Cleft%20%5C%7B%20x%7CAx%3Db%2Cx%5Cgeqslant%200%20%5Cright%20%5C%7D$

非标准形如何转化为标准形？

（1）目标函数是最大化，而不是最小化

将原问题的目标函数乘以（-1），变换后最优解不变

$eq?max%20%5Cquad%20z_%7B1%7D$

令 $eq?z_%7B2%7D%3D-z_%7B1%7D$

可化为 $eq?min%20%5Cquad%20z_%7B2%7D%3D-max%20%5Cquad%20z_%7B1%7D$

（2）线性约束中有大于等于约束，有小于等于约束。

引入松弛变量，剩余变量进行转换

大于等于约束

$eq?%5Csum_%7Bj%3D1%7D%5E%7Bn%7Da_%7Bij%7Dx_%7Bj%7D%5Cgeqslant%20b_%7Bi%7D$

在约束条件左边减去非负松弛条件变量 $eq?x_%7Bn+j%7D$

$eq?%5Csum_%7Bj%3D1%7D%5E%7Bn%7Da_%7Bij%7Dx_%7Bj%7D-x_%7Bn+j%7D%3D%20b_%7Bi%7D$

小于等于约束

$eq?%5Csum_%7Bj%3D1%7D%5E%7Bn%7Da_%7Bij%7Dx_%7Bj%7D%5Cleqslant%20b_%7Bi%7D$

在约束条件左边加上非负松弛条件变量 $eq?x_%7Bn+j%7D$

$eq?%5Csum_%7Bj%3D1%7D%5E%7Bn%7Da_%7Bij%7Dx_%7Bj%7D+x_%7Bn+j%7D%3D%20b_%7Bi%7D$

（3）决策变量无约束，我们称之为自由变量

消除自由变量，引入两个非负变量

假设 $eq?x_%7Bk%7D$ 无约束，可化为标准形，令 $eq?x_%7Bk%7D%3Dx_%7Bk1%7D-x_%7Bk2%7D%2Cx_%7Bk1%7D%2Cx_%7Bk2%7D%5Cgeqslant%200$

（4）目标函数含有绝对值项，消除绝对值符号

已知标准线性规划挑战，如何求解？

可行解:满足所有约束条件的解 $eq?x%3D%28x_%7B1%7D%2Cx_%7B2%7D%2C...%2Cx_%7Bn%7D%29$ 称为线性规划问题的可行解

可行域:所有可行解构成的集合称为问题的可行域，记为 R

最优解:使目标函数达到最小值的可行解叫最优解

基、基向量、基变量、非基向量、非基变量：

设约束方程的系数矩阵A中，有 m个线性无关的列向量记为B=( p1 , p2 ,…, pm )，则 B为该

线性规划的一个基，向量 p1 , p2 ,…, pm 称为 基向量；与之对应的变量x1,x2,...,xm称为

基变量，记为 $eq?x_%7BB%7D%3D%28x_%7B1%7D%2C...%2Cx_%7Bm%7D%29%5E%7BT%7D$ ; 其余的向量为非基向量，记为 N=( pm+1 , pm+2 ,…,pn );

其余的变量为非基变量，记为 $eq?x_%7BN%7D%3D%28x_%7Bm+1%7D%2C...%2Cx_%7Bm+n%7D%29%5E%7BT%7D$

矩阵形式可化为：

$eq?min%20%5Cquad%20z%3Dc%5E%7BT%7Dx$

$eq?s.t.%20%5Cquad%20Ax%3Db%5Crightarrow%20%28B%2CN%29%5Cbinom%7Bx_%7BB%7D%7D%7Bx_%7BN%7D%7D%3Db%5Crightarrow%20Bx_%7BB%7D+Nx_%7BN%7D%3Db$

$eq?x%5Cgeqslant%200$

令自由未知数（非基变量）为0，得 $eq?Bx_%7BB%7D%3Db$

$eq?x_%7BB%7D$ 中各向量线性无关，故存在唯一解 $eq?x_%7BB%7D%3DB%5E%7B-1%7Db$

故唯一解为 $eq?x%3D%5Cbinom%7BB%5E%7B-1%7Db%7D%7B0%7D$ ，也是此方程对应于基底B的一个基本解

基本可行解：解出的基本解，有一部分满足变量的非负约束，即解大于等于0，这些解称为基本可行解；

有些解小于0的，显然不满足大于等于0的条件，这些基解不是可行解，没有用处；

可行基：基本可行解对应的基，称为可行基；

退化的基本可行解：若基本可行解中有一个或多于一个基变量取值为零时，该解为退化的主要可行解；

否则，为 非退化的基本可行解。

a.图解法

注意：图解法不要求化为标准形

b.一般求解步骤

c.MATLAB解法

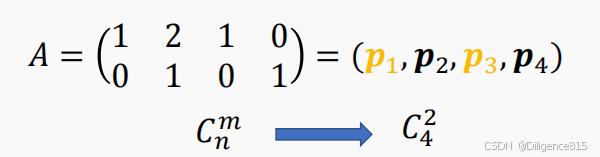
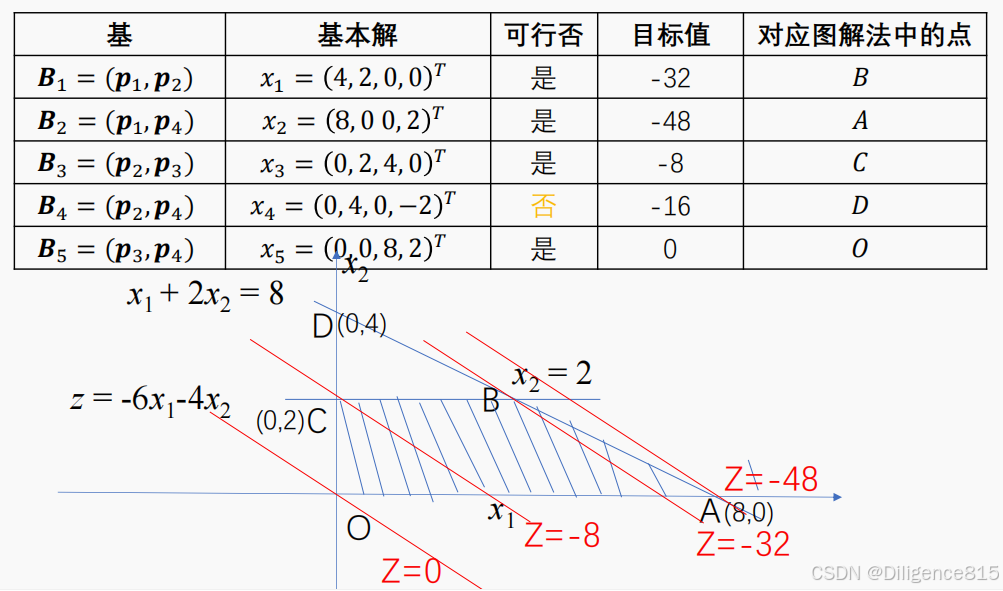
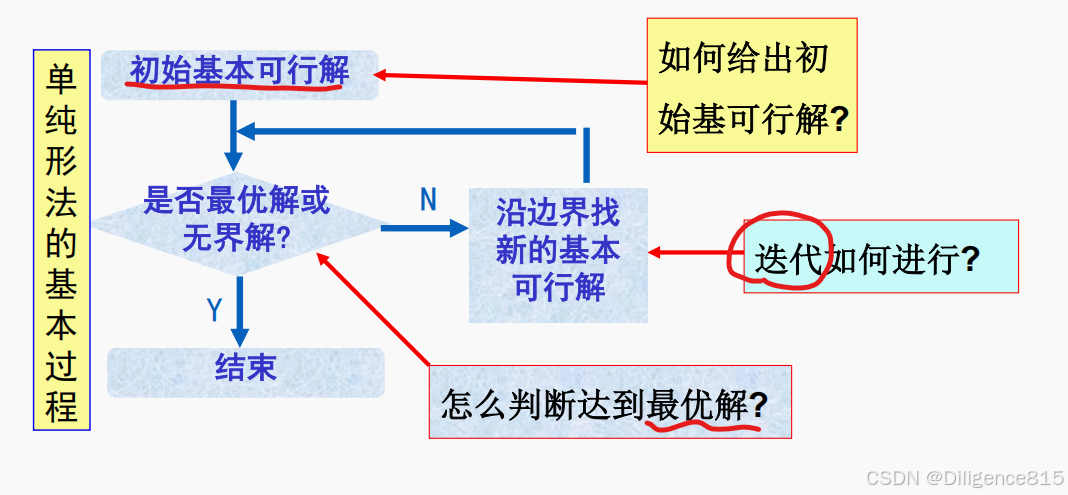
2.线性规划单纯形法

①基本原理

1中所用方法本质上，是一种枚举法，适用于小型规划困难(阶数m≤6和维数n≤5的情况)

单纯形法适用于大型规划问题，其基本思想如下：

从可行域的一个顶点出发，沿着可行域的边界移到另一个相邻的顶点，要求新顶点的目标函数值不比原目标函数值差，如此迭代，直至就是有选择地取（而不是枚举所有的）主要可行解，即

找到最优解，或判定问题无界。

②如何给出初始基可行解？——矩阵运算或者手算法，具体可见习题，大M法，两阶段法

③怎么判断达到最优解？——定理二

④如何迭代？——定理四，满足最小比值原则

先找出根本可行解

表格形式

和公式法类似，但方便了计算

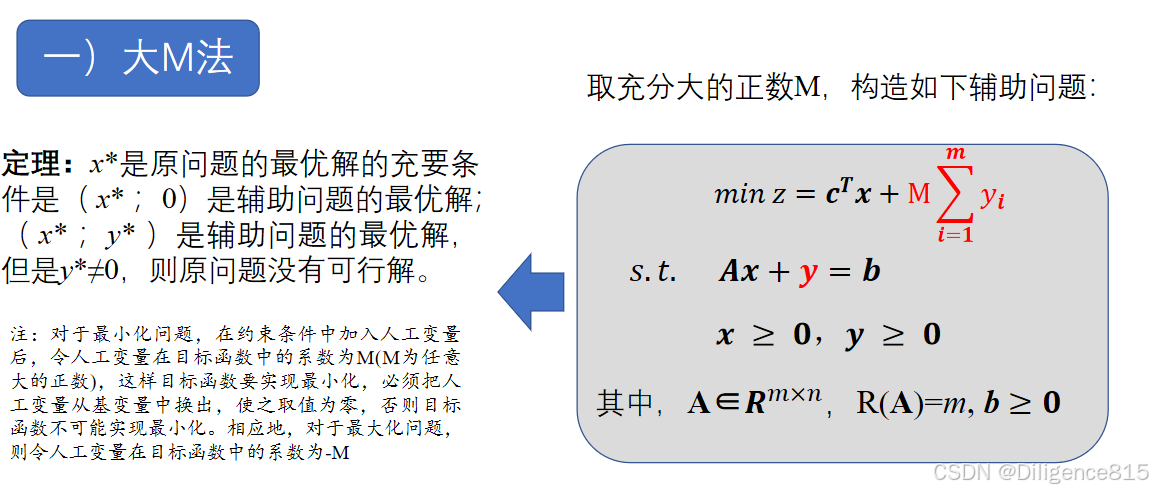
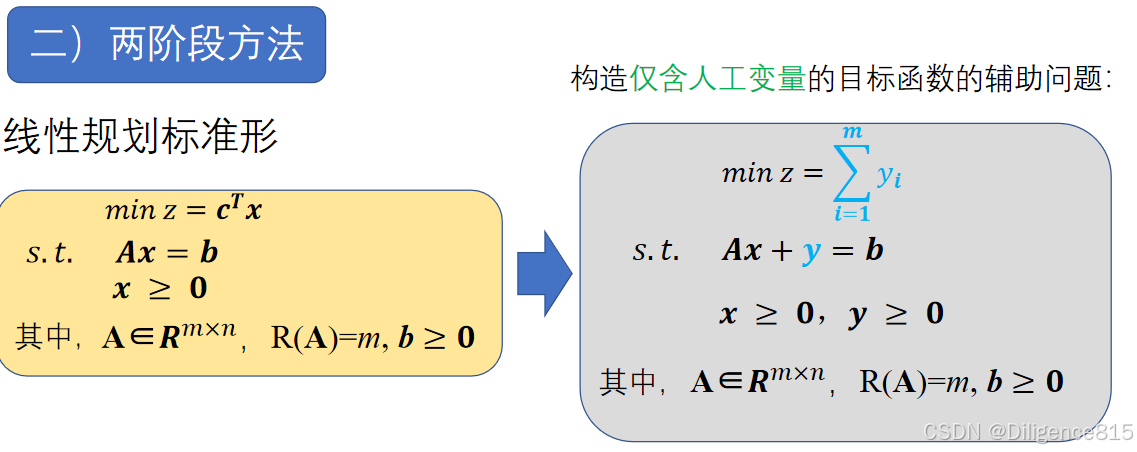
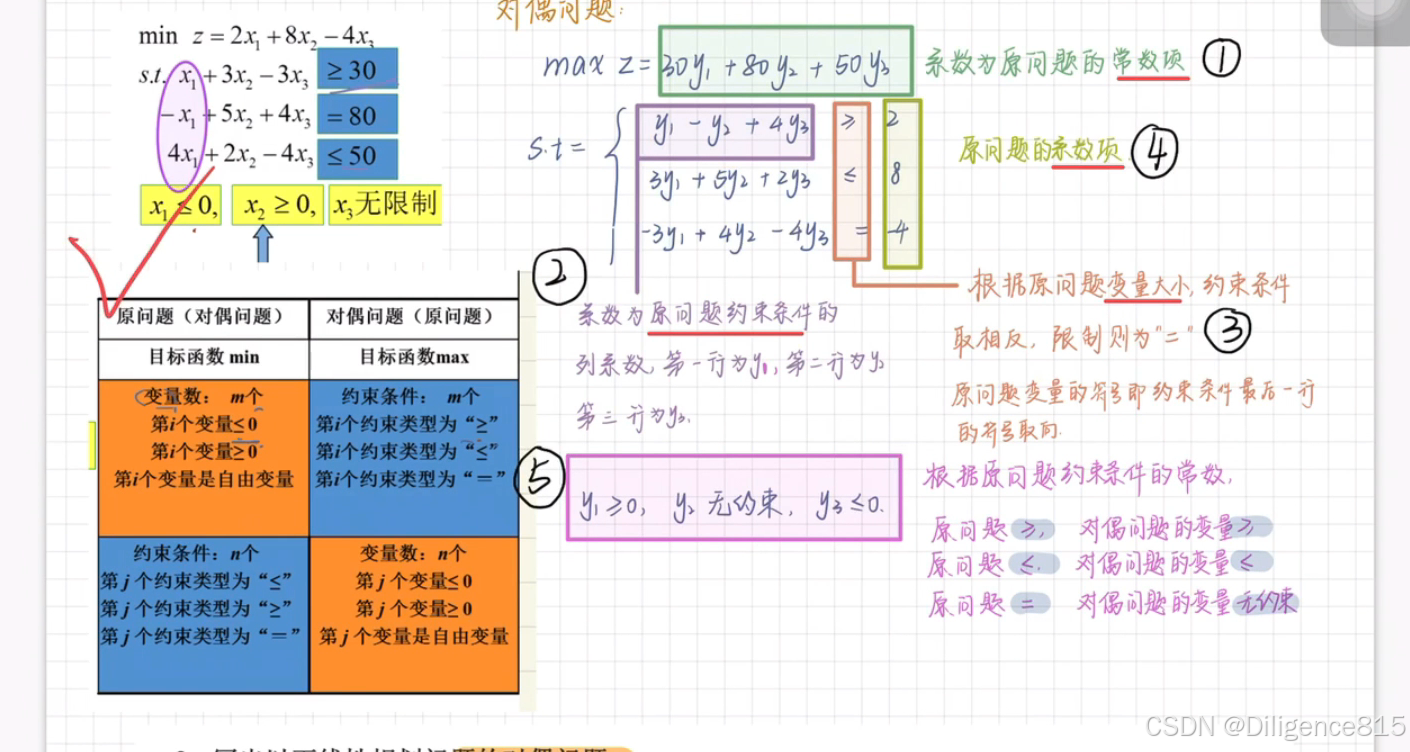
3.线性规划对偶问题

任一线性规划问题都存在另一与之伴随的线性规划难题，它们组成一对互为对偶的线性规划问题线性规划的对偶障碍与原问题互为对偶，线性规划的原问题与对偶问题地位具有对称关系

套模板，具体情况具体分析

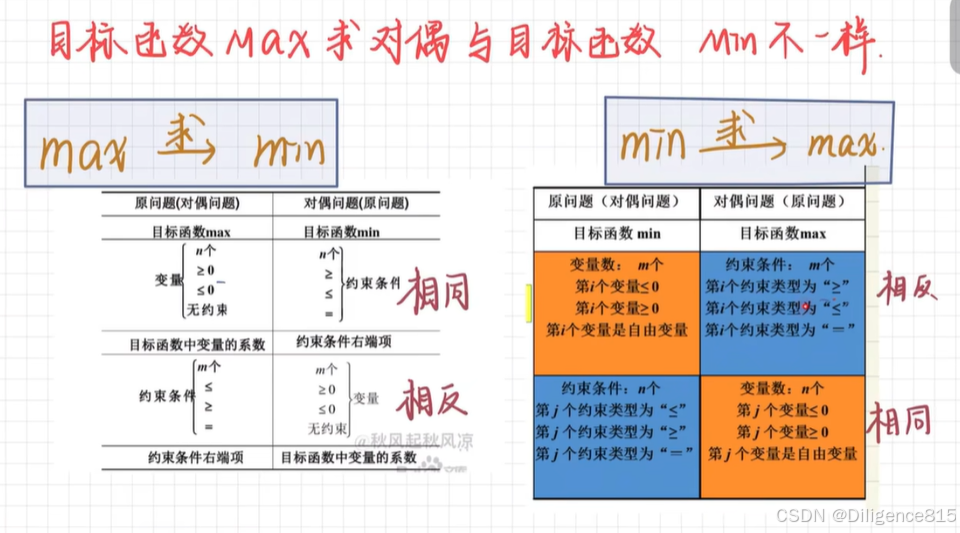
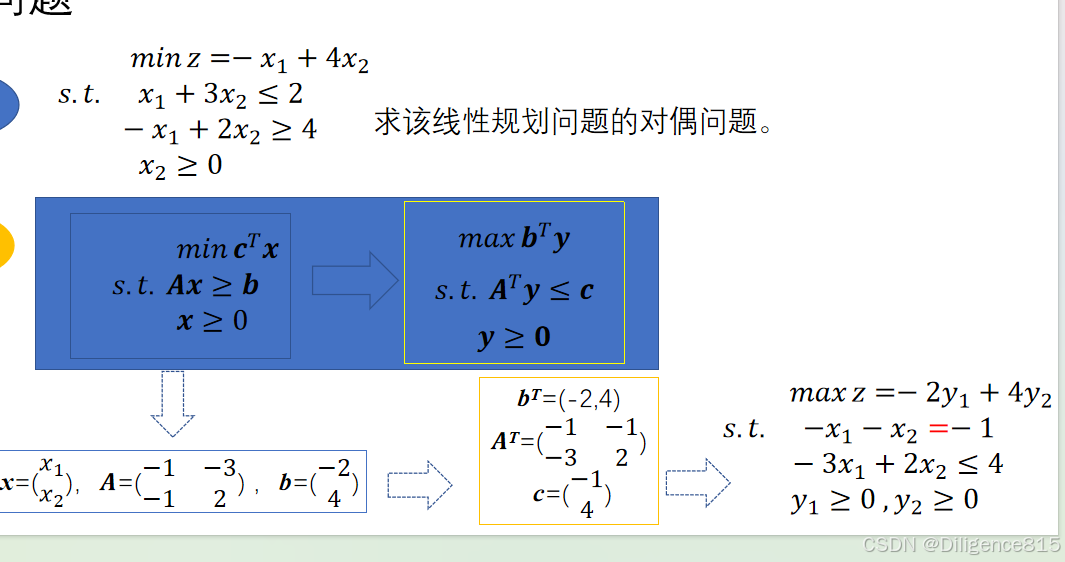
和一堆相关定理，额，要晕了。不想看，来不及了啊啊啊

四、非线性规划问题

目标函数或者约束条件，只要有一个是非线性的，就叫做非线性规划障碍。

常见情况是解析解求不出来或者非常困难，求的是数值解。

1.无约束优化问题

什么？就是障碍形式

$eq?min%20f%28x%29%20%5Cquad%20x%5Cepsilon%20R%5E%7Bn%7D$

怎么求解？迭代法，不断求解点列，直至收敛

a.直接法：只要用到目标函数值，不需要求导数

b.间接法：计算时需要用到目标函数的导数

①信赖域方法：方向与步长合二为一， $eq?x_%7Bk+1%7D%3Dx_%7Bk%7D+p_%7Bk%7D$ ，在一个小的邻域内求

讲的挺好粘在这：https://www.bilibili.com/video/BV1mP411C7ed/?spm_id_from=333.788.videopod.sections&vd_source=c2877adb1381ef6ea843b6c0170c3f69

②线搜索办法：已知方向 $eq?d%5E%7B%28k%29%7D$ ，求步长

$eq?x_%7Bk+1%7D%3Dx_%7Bk%7D+%5Calpha%20_%7Bk%7Dd_%7Bk%7D%2C%5Calpha%20_%7Bk%7D%5Cgeq%200$

$eq?%5Calpha%20_%7Bk%7D%3Dargmin%20f%28x_%7Bk%7D+%5Calpha%20_%7Bk%7Dd_%7Bk%7D%29%2C%5Calpha%20_%7Bk%7D%3E%3D0$

一阶精确线搜索法：要计算大量梯度及导数值

一阶非精确线搜索法：

6.梯度法/最速下降法

7.共轭梯度法

不考

2.约束优化挑战

困难模型是什么？

$eq?min%20%5Cquad%20f%28x%29$

$eq?s.t.%20%5Cquad%20g_%7Bi%7D%28x%29%5Cleq%200$

$eq?h_%7Bj%7D%28x%29%3D0$

如何求解？

（1）直接法：可行域直接求解目标函数最优解，初始点、迭代方向、步长，同时保证可行性

直接搜索法：对约束优化挑战不预先做转换，对目标函数导数的存在无要求；随机方向、约束坐标轮换、复合形法

可行方向法：可行点，迭代，得到新的可行点；转化为无约束了

（2）间接法：约束优化转化为无约束优化，可求解等式加不等式约束

序列二次规划：用二次函数逼近目标函数；SLP,SQP

惩罚函数法：序列无约束优化，构造增广目标函数，将约束问题转化为无约束挑战；

什么？就是要达到什么目标——其最优性条件

对于等式约束：引入拉格朗日乘子，满足微分条件=0的点即为局部最优解

对于不等式约束：KT条件

一般的约束问题：KKT条件，最优解的必要条件，对于凸规划问题就是充要条件了

KKT的推导：

先不考虑非等式约束 $eq?g%28x%29$ ，求其最优条件 $eq?x%5E%7B*%7D$

代入，可能有

① $eq?g%28x%5E%7B*%7D%29%3E%200$ 不满足，应舍弃，那新的解在哪里呢？

② $eq?g%28x%5E%7B*%7D%29%3C%200$ 正好满足，但是此时约束没起作用！为无约束求解问题,此时 $eq?%5Clambda%3D%200$

③ $eq?g%28x%5E%7B*%7D%29%3D%200$ 转化为等式约束，引入拉格朗日乘子 $eq?%5Clambda%5Cgeq%200$

将②③统一形式 $eq?%5Clambda%20g%28x%29%3D0$ ，两者必有一为0

KKT的应用：

等式求最优，不等式验证

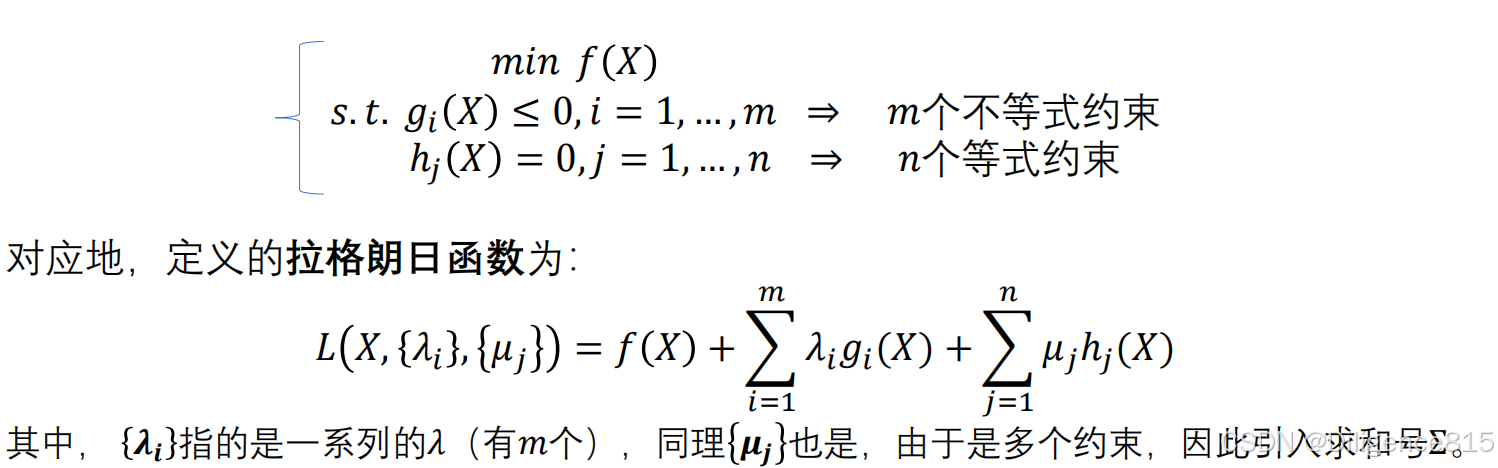
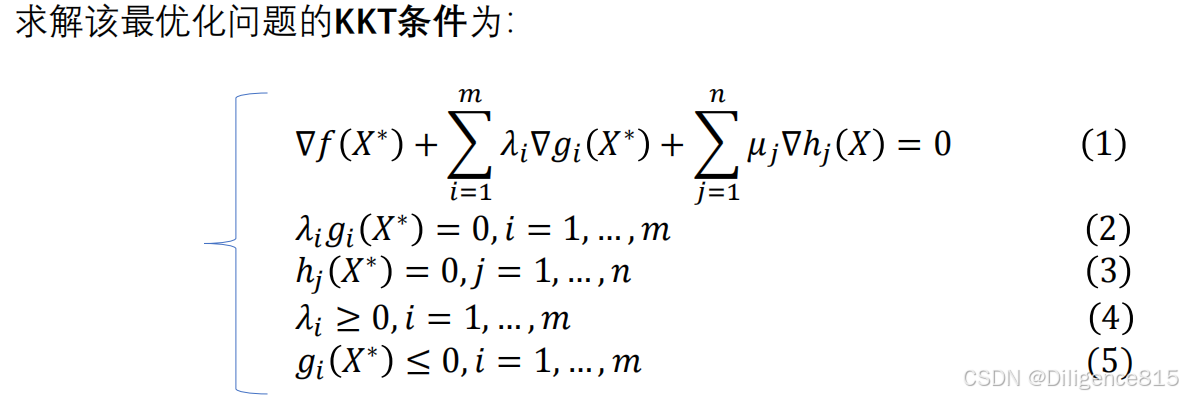
求KKT点并验证的典型例子：

约束优化算法——惩罚函数法

加入惩罚函数，将挑战转化为一个无约束优化问题

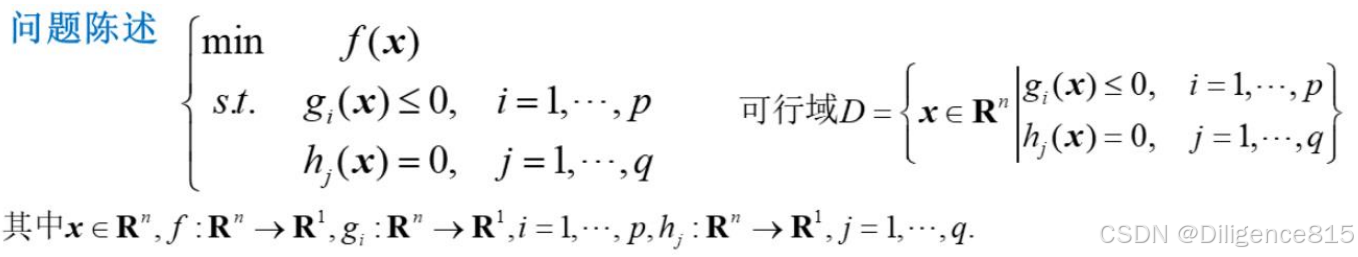
外点法/罚函数：出界，罚

小于或等于对应max

构造增广的目标函数，加入惩罚函数 $eq?p_%7Bc%7D%28x%29%3Dc%5Csum_%7Bi%3D1%7D%5E%7Bp%7D%5Bmax%28g_%7Bi%7D%28x%29%2C0%29%5D%5E%7B2%7D+%5Cfrac%7Bc%7D%7B2%7D%5Csum_%7Bj%3D1%7D%5E%7Bq%7D%5Bh_%7Bj%7D%28x%29%5D%5E%7B2%7D$

问题转化为 $eq?min%20%5Cquad%20F_%7Bc%7D%28x%29%3Df%28x%29+p_%7Bc%7D%28x%29$

之后再用某种无约束优化算法求解

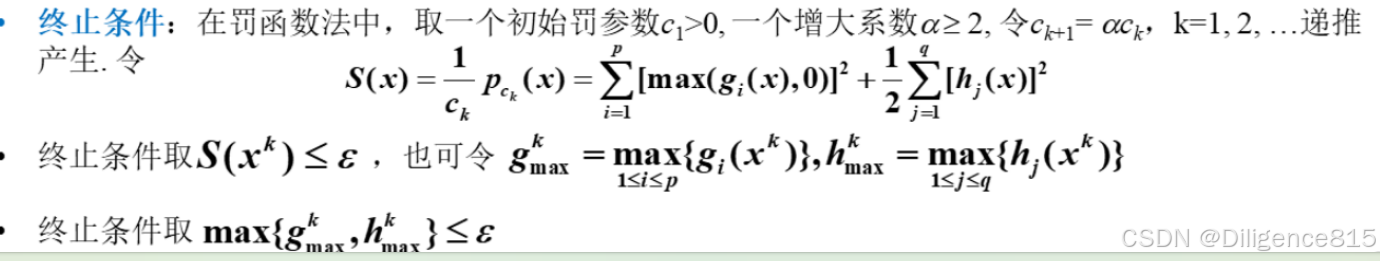
内点法/障碍函数法：仅不等约束，从可行域内部趋于边界

乘子法

六、多目标优化问题

1.多目标规划概念

同时存在多个最大化或最小化的目标函数，并且目标函数之间并不是相互独立的，也不是相互和谐融洽的，或多或少会存在冲突，使其不能同时满足所有的目标函数。

由于存在冲突，只能使多个子目标尽可能地都达到最优化。

解非唯一，存在一组由众多 Pareto最优解组成的最优解集合 ,集合中的各个元素称为 Pareto最优解或非劣最优解

都有可能是不存在的

2.多目标规划典型实例

同时达到最优举例。工厂

3.多目标规划求解方法

目标规范化：归一化

绝对最优解：一般不存在，是所有优化目标的公共解

解集：

4.求解

约束法：确定主导目标，转换为单目标

评价函数法：h(F(x))，F(x)为原多目标函数

理想点：分别计算最优解集合，找最接近的。最短距离理想点

加权法：分别求下界

最优化求解的问题，给你一些办法，感觉偏理论，对实际应用涉及较少就是其实就

posted @ 2025-10-29 16:10 yangykaifa 阅读(12) 评论(0) 收藏举报

刷新页面返回顶部