【论文阅读】3D Graph Convolutional Networks with Temporal Graphs A Spatial Information Free Framework For Traffic Forecasting
3D Graph Convolutional Networks with Temporal Graphs A Spatial Information Free Framework For Traffic Forecasting
论文基本信息
- 标题：3D Graph Convolutional Networks with Temporal Graphs: A Spatial Information Free Framework For Traffic Forecasting
- 发表日期：3 Mar 2019
- arXiv：1903.00919v1 [cs.LG] 3 Mar 2019
- 作者：
- Bing Yu
- Mengzhang Li
- Jiyong Zhang
- Zhanxing Zhu
解决什么问题
解决了以下三个现存交通预测模型中存在的问题：
- 时空卷积忽略了时间和空间动态性的相互影响：STGCN在空间上使用图卷积，在时间轴上使用一维卷积，但是对时间和空间信息进行单独处理，忽略了空间和时间动态性之间的相互影响。
- 空间信息难以获取：现存的基于图的预测方法使用空间距离或道路连接来构造图，但是一些实践场景中，由于自由编辑地图无法保证实时更新和准确性，导致空间邻接矩阵很难构造；而商业地图服务又昂贵，api也会限制距离计算。
- 忽略了时间模式的相似性：使用空间信息构建邻接矩阵忽略了时间模式的相似性，距离很远的地点可能拥有相似的时间模式，比如办公建筑附近都会在高峰时期产生交通拥堵。
怎么解决问题
- 使用三维图卷积对静态的道路图和时间动态性一起学习。
- 使用动态时间规整度量时间序列相似度，使用节点间时间相似度来构造邻接矩阵。
实验
- 数据集：
- PeMSD7
- PEMS-BAY
原理
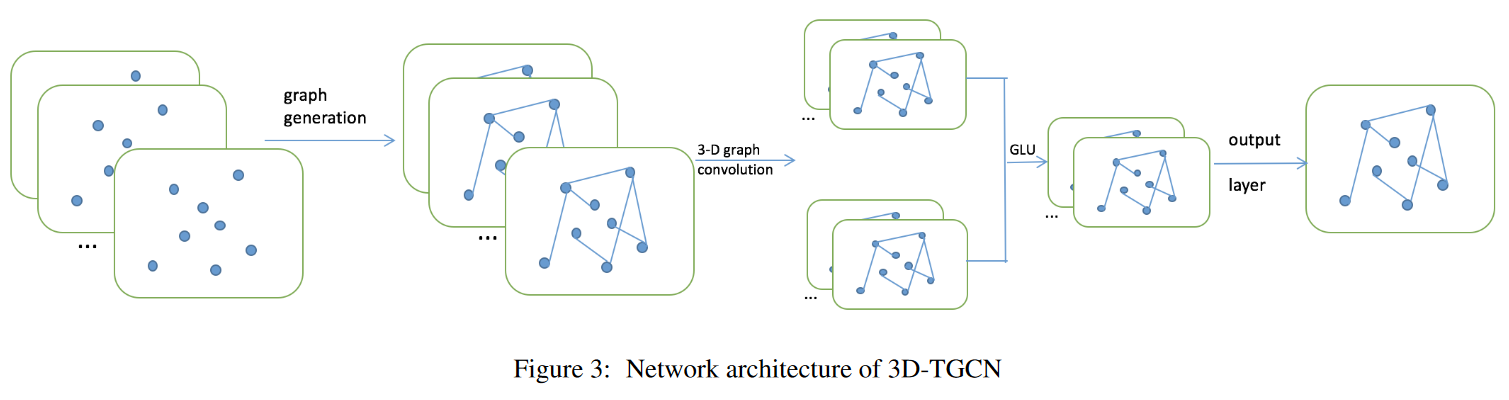
- 时间图生成：
- 使用DTW（动态时间规整算法）计算节点之间的时间序列相似度。
- 对每一个节点，取相似度前5%的节点连接，构造邻接矩阵。
- 3D-TGCN：
-
\[\hat{X}_{t,C_o}=\sum_{i=1}^{C_i}\sum_{t'=0}^{K_t-1}\sum_{k=0}^{K-1}\theta_{i,C_o,k,t'}\widetilde{L}^kX_{(t-t'),i},t=K_t,K_{t+1},...,M \]
- \(1\le t\le M\)，其中，M是时间序列的长度。
- \(C_i, C_o\)：这一三维卷积层的输入和输出的大小（也就是每个节点上特征的数量）。
- \(\theta_{i,C_o,k,t'}\)：这一层每个输出通道需要训练的参数。
- \(\Theta_{*\mathcal{G}}X\)：卷积符号，其中参数\(\Theta\in\mathbb{R}^{C_i\times C_o\times K_t\times K}\)。
-
- GLU线性门控单元：
- 将卷积输出的所有通道分成两等份，一份为G，另一份为H，GLU的输出为：\(\hat{X}=G\odot\sigma(H)\in\mathbb{R}^{(M-K_t+1)\times C_o}\)，其中\(\odot\)是哈达玛积，\(\sigma\)是sigmoid函数。
- 将3D卷积和GLU合起来作为3D图卷积层。
- 损失函数：
-
\[L(\hat{X};\Delta_\theta)=\sum_{t}(\frac{1}{2}\parallel\hat{X}_{t+H}-X_{t+H}\parallel_2^2+\parallel\hat{X}_{T+H}-X_{T+H}\parallel_1) \]
-
代码
由于原文没有提供代码、详细数据集或数据处理方法，难以复现。
