斜率优化讲解
斜率优化讲解
——by ysy
一、简单的复习
我在这里给出一个式子,\(f[i]=max(g[i]+calc(j))\),这是绝大部分dp式子的最基本的模型,每一道题可能只是将\(max\)改为\(min\),或者是将calc中的东西更改一下,大家思考一下是不是这样的。
如果当calc之中的每一项都只含有\(i\)或者是\(j\),并且这两个字母没有相乘的情况我们就可以用单调队列,这个不难理解,举个例子,像下面的这个式子:\(f[i]=max \{ f[j]+a∗num[j] \}\),就可以用单调队列维护,因为整个式子之中只有关于\(i\)的单独项和关于\(j\)的单独项。
但是像这样的式子就不可以了:\(f[i]=max \{ f[j]+(sum[i]+sum[j])^2 \}\),因为这个式子展开后就会出现关于\(i\)的式子乘上关于\(j\)的式子。像这样的式子就是斜率优化的适用范围。
二、斜率优化
像斜率优化这样知识点需要一道例题来进行讲解。下面我们来看一道经典的例题。
1.列方程
我们先想这道题的dp式子,先不管时间复杂度的问题。
这个式子应该很好想:\(f[i]=min \{ f[j]+( \sum_{k=j+1}^{i} lenth[k] +i−j−l)^{2} \}\),我们来分析一下时间复杂度:\(O(n^3)\)。
想一下优化,我们是不是可以将求和部分写成前缀和的形式?将\(\sum\)的部分化成\(sum[i]\)。这样我们就可以将式子转化成\(f[i]=min \{ f[j]+( sum[i] -sum[j] +i−j−l)^{2} \}\),这样的话时间复杂度就降低成为\(O(n^2)\)。时间是更低了,但是还是过不了啊,这是我们就要等价地变换式子,使其成为y=kx+b的形式,这个形式就是斜率优化的核心。
2.转化式子
\(f[i]=min \{ f[j]+( sum[i] -sum[j] +i−j−l)^{2} \} \downarrow\)
\(f[i]= f[j] + [ ( sum[i] + i ) - ( sum[j] + j ) - l ]^2 \downarrow\)
令\(s[i]=sum[i]+i \downarrow\)
\(f[i]=f[j]+( s[i] -s[j] - l)^2\)
\(f[i] = f[j] + s[i]^2 + ( s[j] + l ) ^2 - 2\times s[i] \times ( s[j] + l) \downarrow\)
\(f[j] + s[i]^2 + ( s[j] + l )^2 = 2 \times s[i] \times ( s[j] +l ) + f[i]\)
3.分析式子
\(f[j] + s[i]^2 + ( s[j] + l )^2 = 2 \times s[i] \times ( s[j] +l ) + f[i]\)
观察上面的式子,我们发现这个式子十分像一种函数,y=kx+b,可能大家会有疑问,这个式子和直线的表达是有什么形似之处呢?
我们将\(f[j] + s[i]^2 + (s[j] + l)^2\)这个部分看做一个整体记为\(y\),这个部分可以看成一个整体的条件是:这个整体中的所有部分都是已求出的,并且当知道\(i\)和\(j\)之后可以\(O(1)\)求出。显然这个整体满足。同理我们将\(2 \times s[i]\)和\((s[i] + l)\)这两个部分也分别看做整体,并分别记为\(k\)、\(x\)。这样式子就化为\(y=kx+f[i]\)。
下一步,我们建立以个平面直角坐标系,这个平面直角坐标系中的每一个点的坐标\((x,y) \)都对应的是上面式子中的\(x \)和\(y \),这样我们就能够将每一个与\(i \)有关的东西处理完事之后标到平面直角坐标系之中。每一个点的坐标表成\(( s[i],f[i] + (s[i] + l)^2 ) \),可能有人会问为什么纵坐标没有了\(s[i]^2 \),并且横坐标没有了\(l \),这个问题下面会解答,请稍作等待。
如果我们想用\(j\)来转移\(i\)的话,就要让斜率为\(2 \times s[i]\)的直线过点\((s[j],f[j] + (s[j] + l)^2)\),并且此时直线的截距就是新的\(f[i]\),因为\(f[i]\)为这条直线的\(b\)。再看下面的图解,我们将求过的点都标到平面直角坐标系中,我们可以发现,我们想过的这个点一定在我们维护的大圆包上,像点2这样的点就不能被用来更新,因为过点3所得截距,一定比过点2所得截距小,那么我们能发现当点3求出之后,只要比较一下,点2和点3形成的直线的斜率和点1和点2形成的直线的斜率,如果2、3形成的比1、2形成的要小,那么3号点一定比2号点更优。我们再看,假设下图之中已经维护好1到5的所有点,那么就会出现这样的大圆包。我们用求出6的点的直线去和这些点相交,我们发现只有点4在当前直线上时能使截距最小(画一画图就能发现是过点4时,直线的截距最小),根据是由点4转移,我们可以发现,当两个点1、3的斜率小于\(2 \times s[i]\)的时候,横坐标小的点一定不能用来转移,同理斜率大于\(2 \times s[i]\)的两个点,横坐标大的也不能够用来转移,这个性质是不是很好?
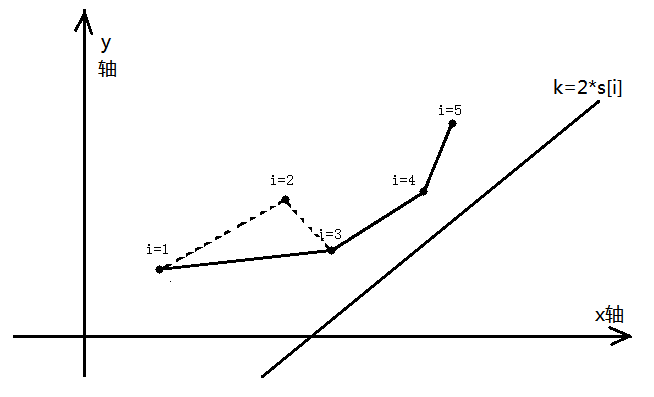
根据上面我们发现的式子,我们可以维护一个类似于单调队列的队列来维护我们的大圆包。但是这个大圆包具体怎么维护呢?我们先看如何求斜率。如果给你直线上的两个点,我想大家一定会求斜率。就是两点的纵坐标相减的差除上两点的横坐标相减的差。这里也就解释了,为什么上文中的纵坐标没有了\(s[i]^2\),因为两式相减时\(s[i]\)是相同的,从而\(s[i]^2\)也就是相同的,所以相减时就将其减掉了,因此\(s[i]^2\)不用出现在纵坐标之中。同理在相减时我们的横坐标也不需要\(l\)。
double re_x(int i){return s[i];}
double re_y(int i){return f[i]+(s[i]+l)*(s[i]+l);}
double re_k(int i,int j){return (re_y(j)-re_y(i))/(re_x(j)-re_x(i));}
会求斜率了,我们再来看怎么维护大圆包,我们发现当队列中最后一个的点和队列中倒数第二个点的产生斜率大于最后一个点和新产生的点产生的斜率,那么结尾就要弹出队列,这个用一个\(whlie\)循环就能够解决,最后再将新产生的点放在结尾。这个实现十分像单调队列的实现。
int main()
{
while(head<tail&&re_k(q[tail],i)<re_k(q[tail],q[tail-1])) tail--;
q[++tail]=i;
}
我们再看,怎么满足第二个性质,让更新变成\(O(1)\)的?我们发现当队列中第一个点和第二个点产生的斜率如果小于当前的直线,那么第二个点更新一定比第一个点更新更优,我们就要进行队首弹出。这个过程也十分像单调队列的维护。最后直接用队首进行更新。
int main()
{
while(head<tail&&re_k(q[head],q[head+1])<2*s[i]) head++;
f[i]=f[q[head]]+(s[i]-s[q[head]]-l-1)*(s[i]-s[q[head]]-l-1);
}
这样我们就解决了维护的问题,最后就是将这些组装在一起,形成下方的代码。
#include <stdio.h>
#define N 50001
int n,l,head,tail;
long long f[N],s[N],q[N];
double re_x(int i){return s[i];}
double re_y(int i){return f[i]+(s[i]+l)*(s[i]+l);}
double re_k(int i,int j){return (re_y(j)-re_y(i))/(re_x(j)-re_x(i));}
int main()
{
scanf("%d%d",&n,&l);
for(int i=1;i<=n;i++)
scanf("%lld",&s[i]),s[i]+=s[i-1];
for(int i=1;i<=n;i++) s[i]+=i;
q[tail]=0;
for(int i=1;i<=n;i++)
{
while(head<tail&&re_k(q[head],q[head+1])<2*s[i]) head++;
f[i]=f[q[head]]+(s[i]-s[q[head]]-l-1)*(s[i]-s[q[head]]-l-1);
while(head<tail&&re_k(q[tail],i)<re_k(q[tail],q[tail-1])) tail--;
q[++tail]=i;
}
printf("%lld\n",f[n]);
}
4.分析上方代码的适用范围
上方的代码是有一定的适用范围的,大家想一下,为什么我们敢弹出队首与队尾?
我们再来看一下题目,这个题目显然满足一个特点,就是由于我们将\(s[i]\)定义为前缀和,所以他一定是单调递增的,并且我们的点的横坐标也是\(s[i]\)也满足单调递增。这两个性质十分好。我们把队首的元素弹出的条件是斜率小于\(2 \times s[i]\),因为\(s[i]\)满足单调递增,所以弹出时小于,那以后就一定一直小于下去,所以弹出就弹出了。我们再看,因为我们的橫坐标满足单调递增,所以每一次插入点都会在最后,因此结尾弹出也是正确的。
但是如果斜率没有单调性呢?我们就不能将队首弹出,这样我们就不能在\(O(1)\)的时间内求出新的元素,我们可以在大圆包上进行二分。我们看下面的大圆包,会发现只有当前点和上一个点的斜率小于直线斜率,并且和下一个点的斜率大于直线的斜率时,这个点才是最优的。所以我们可以进行二分查找。
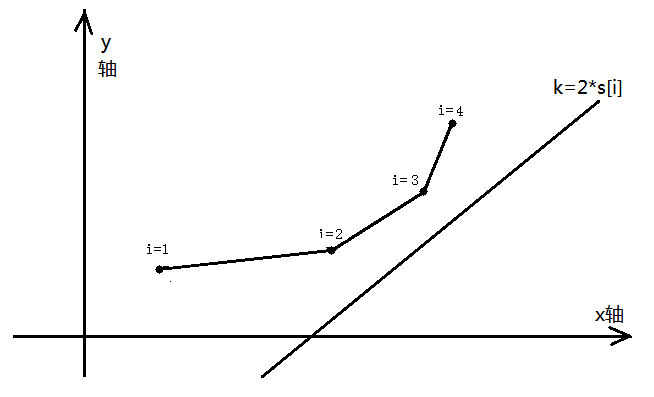
如果我们的横坐标没有单调性呢?我们就不能够将队尾删掉了,我们应该用平衡树来维护,动态维护大圆包。但是怎么维护呢?我们可以运用\(splay\),具体请听本人口述。
三、练习
1.仓库建设
\(1)\)列方程,并转化形式
\(f[i] = min ( f[j] + x[i] \times ( P[i] - P[j]) + g[i] - g[j] + c[i]) \downarrow\)
$ f[i] = f[j] + x[i] \times P[i] - x[i] \times P[j] +g[i] -g[j] +c[i] \downarrow$
\(f[j] - g[j] + x[i] \times P[i] +g[i] + c[i] = x[i] \times P[j] + f[i]\)
\(2) \)找点
显然这里的点就是\(( f[j] - g[j] ,P[j] )\),斜率就是\(x[i]\),截距就是\(f[i]\)。
\(3)\)写吧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号