作者:邬杨明
1 # 模拟退火算法求解三十城市TSP问题
2 # 2018-3-21
3 # yangmingustb@outlook.com
4
5
6 import math
7 import random
8 import datetime
9 import copy
10 import matplotlib.pyplot as plt
11
12
13 class SaTSP(object):
14
15 def __init__(self, tf=0.01, alpha=0.9):
16 self.tf = tf # 最低温度
17 self.alpha = alpha # 降温系数
18 self.iter_num = [] # 记录迭代次数
19 self.distance_path = [] # 记录每一步迭代出来的路径长度
20 self.ultimate_path = []
21 # 30城市坐标
22 self.coordinates = [[41, 94], [37, 84], [54, 67], [25, 62], [7, 64],
23 [2, 99], [68, 58], [71, 44], [54, 62], [83, 69],
24 [64, 60], [18, 54], [22, 60], [83, 46], [91, 38],
25 [25, 38], [24, 42], [58, 69], [71, 71], [74, 78],
26 [87, 76], [18, 40], [13, 40], [82, 7], [62, 32],
27 [58, 35], [45, 21], [41, 26], [44, 35], [4, 50]
28 ]
29
30 self.iteration = 200 * len(self.coordinates) # 每一个温度过程中迭代次数,马氏链长度
31
32 def initial_temperature(self): # 温度初始化,采用t0=-delta(f)/(ln0.9)
33
34 dist_list = []
35 for i in range(100): # 生成一百条路径
36
37 path = random.sample(self.coordinates, len(self.coordinates)) # 生成一条随机序列
38 dist_list.append(self.all_dist(path))
39
40 t0 = -(max(dist_list) - min(dist_list)) / math.log(0.9) # 设置初温
41 print('初始温度是:', t0)
42 return t0
43
44 def D_value(self, current_path, update_path): # 变换前后目标函数差值
45
46 # print('计算两个状态的差值...')
47 current_distance = self.all_dist(current_path)
48 # print('当前距离', current_distance)
49
50 update_distance = self.all_dist(update_path)
51 # print(update_distance)
52
53 d_value = update_distance - current_distance
54 return d_value
55
56 def first_path(self): # 生成第一条初始化的路径
57 length = len(self.coordinates)
58 # 因为对初值不敏感,生成一条随机序列, 第一条路径是随机的
59 path = random.sample(self.coordinates, length)
60 return path
61
62 # 随机交换2个城市顺序,这一步非常重要,调试了五个小时一直不收敛,
63 # 深入理解深拷贝和浅拷贝的区别,注意内存中的变化
64 def swap(self, path):
65 # print('产生新解...')
66 city_1 = random.randint(1, len(self.coordinates) - 1) # 产生第一个交换点
67 while True:
68 city_2 = random.randint(1, len(self.coordinates) - 1) # 产生第二个交换点
69 if city_2 != city_1:
70 break
71 else:
72 continue
73 path[city_1], path[city_2] = path[city_2], path[city_1]
74 # print('产生新解结束')
75 return path
76
77 # 计算两个点之间的距离
78 def two_point_dist(self, point1, point2):
79
80 dist_x = point1[0] - point2[0]
81 dist_y = point1[1] - point2[1]
82 dist = dist_x ** 2 + dist_y ** 2
83 dist = math.sqrt(dist)
84 return dist
85
86 def all_dist(self, path): # 计算所有点距离,总共30段距离
87 sum_cities = 0
88 n = len(path)
89 for i in range(n - 1): # 先计算前29段距离
90 sum_cities += self.two_point_dist(path[i], path[i + 1])
91 sum_cities += self.two_point_dist(path[n - 1], path[0]) # 计算第30个点和第一个点的距离,形成闭环
92 return sum_cities
93
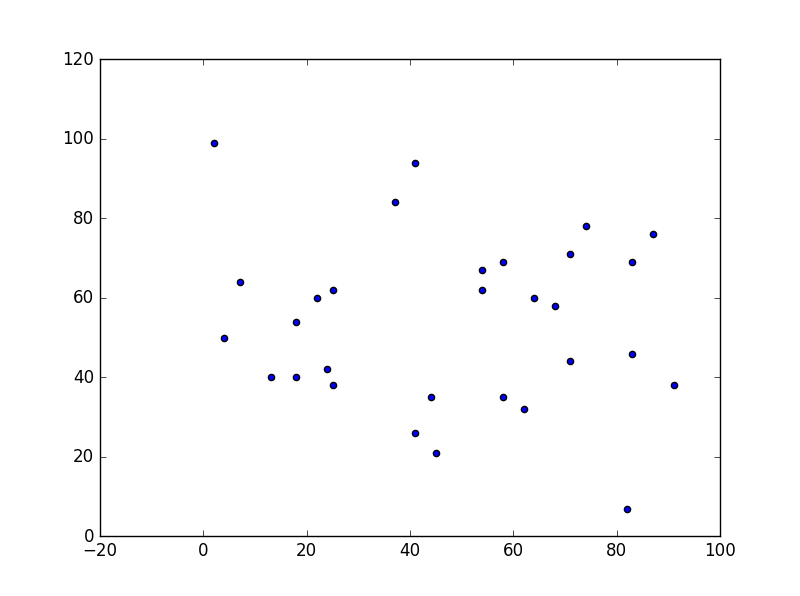
94 def city_scatter(self): # 画出城市分布散点图
95 city_x = []
96 city_y = []
97 for i in self.coordinates:
98 city_x.append(i[0])
99 city_y.append(i[1])
100 plt.scatter(city_x, city_y)
101 plt.show()
102
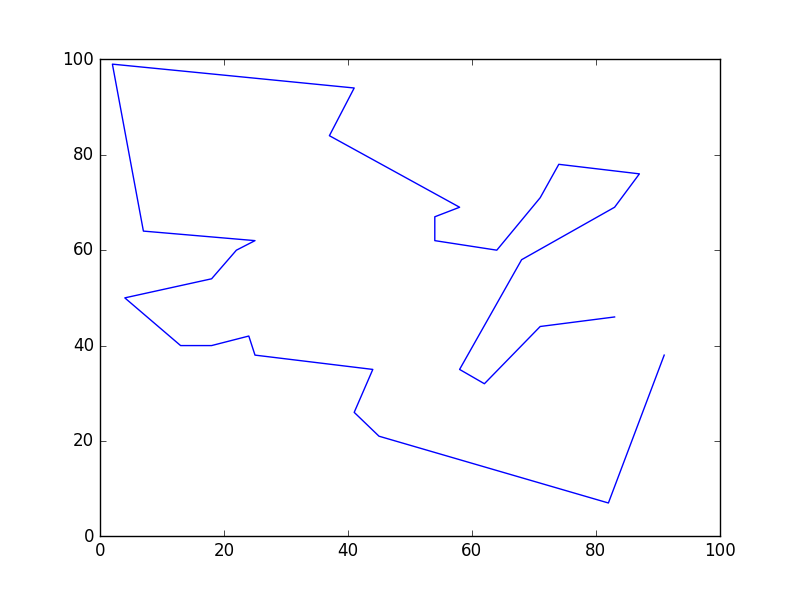
103 def city_plot(self, path): # 画出最终路径图
104 city_x = []
105 city_y = []
106 for i in path:
107 city_x.append(i[0])
108 city_y.append(i[1])
109 plt.plot(city_x, city_y)
110 plt.show()
111
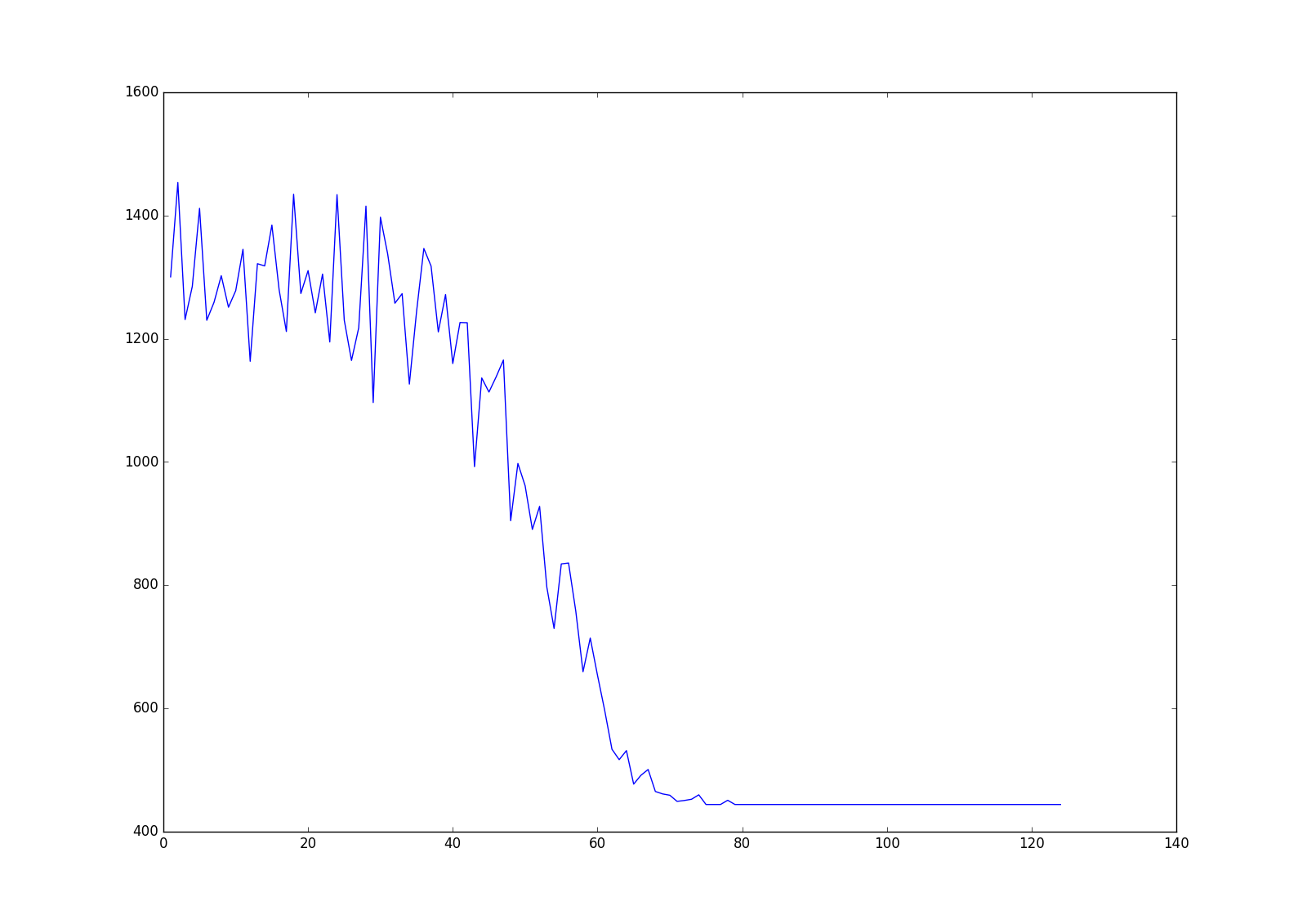
112 def plot_graphic(self): # 画出路径长度随迭代次数变化曲线图
113 plt.plot(self.iter_num, self.distance_path)
114 plt.show()
115
116 def main(self): # 函数式编程,调用其它函数,进入这个大循环
117
118 start_time = datetime.datetime.now() # 增加时间模块,计算运行时间
119 t = self.initial_temperature() # 调用生成初温函数
120 current_path = self.first_path()
121 # print(current_path)
122 i = 0
123 while t > self.tf: # 终止条件
124 iteration_number = 0
125 while iteration_number < self.iteration: # metropolis终止条件
126 # a = self.all_dist(current_path)
127 temple_path = copy.deepcopy(current_path) # 建立一个当前路径临时列表,防止改变当前路径值
128 update_path = self.swap(temple_path)
129 # print(update_path)
130 de2 = self.D_value(current_path, update_path)
131 # print(de,de2)
132
133 if de2 < 0: # 如果增量为负值,则接受
134
135 current_path = update_path
136 # print(current_path)
137
138 else: # 产生新解比较
139 p = math.exp(-de2 / t)
140 if random.random() <= p:
141 current_path = update_path
142 # print(current_path)
143
144 else: # 否则保留当前解解,而不是一直产生新解比较,注意误区
145 current_path = current_path
146 # else:
147 iteration_number += 1
148
149 t = self.alpha * t
150
151 i = i + 1
152 self.iter_num.append(i)
153 self.ultimate_path = current_path
154 distance = self.all_dist(current_path)
155 self.distance_path.append(distance) # 路径长度存入列表
156 # print(distance)
157
158 end_time = datetime.datetime.now()
159 this_time = end_time - start_time
160 print('程序运行时间:', this_time)
161
162 self.city_scatter()
163 self.city_plot(self.ultimate_path)
164
165
166 s1 = SaTSP()
167
168 s1.main()
![]()
![]()
![]()






 浙公网安备 33010602011771号
浙公网安备 33010602011771号