时间复杂度和空间复杂度

时间复杂度

• 定义：指执行这个算法所需要的计算工作量（CPU）
• 常见的复杂度有：
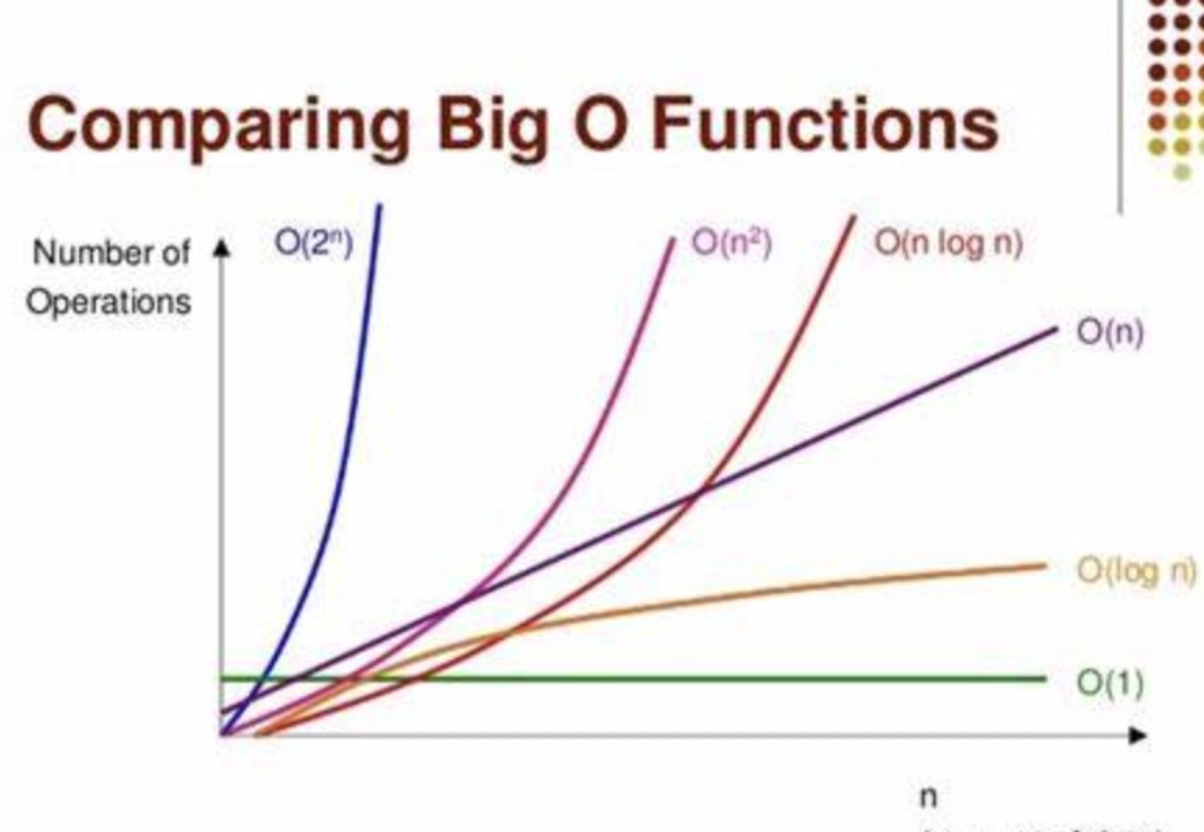
  • O(1) 常数型 -- 无循环
  • O(log n)  对数型 -- 二分法
  • O(n)  线性型 -- 单次循环　
  • O(nlogn) 线性对数型 -- 单次循环 + 二分法
  • O(n^2) 平方型 -- 嵌套循环 
  • O(n^3) 立方形 -- 三层嵌套循环 （不常见）
  • O（n^k）k次方型 （不常见）
  • O(2^n) 指数型（不常见）

　　　　　　　　

　　　　注意：如果用到的 API，要结合数据结构去分析复杂度，看到代码的本质

　　　　如：数组的 unshift、shift、splice 本身就是一个O(n) 的复杂度，如果代码中有用到，要把API本身的复杂度算进去

空间复杂度　

• 定义：指执行算法所需的内存大小。额外需要定义多少变量
• 常见的空间复杂度：
  • O(1) -- 定义了为数不多的变量，和 n 无关
  • O(n) -- 需定义和 n级别的变量，如而外符值一个同样的数组
  • 其他都不常见　　

前端重时间、轻空间。优先考虑时间复杂度