并查集

它最重要的作用就是用来：检查一个图是否存在环。

   

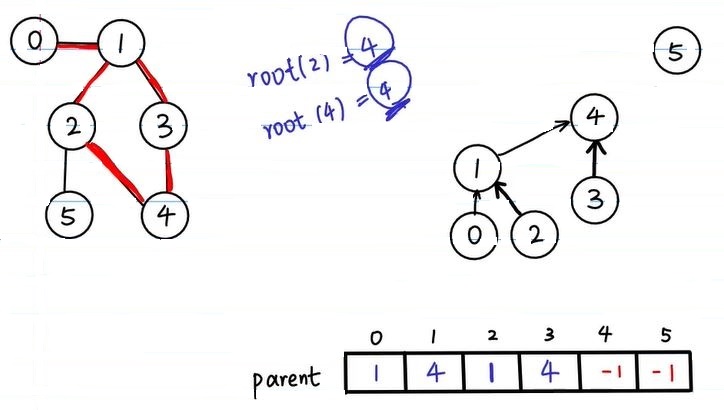
#define VERTICES 6

void Init(int parent[], int rank[])
{
    for (int i = 0; i < VERTICES; ++i) {
        parent[i] = -1;
        rank[i] = 0;     // 代表当前树高
    }
}

int FindRoot(int x, int parent[])
{
    int x_root = x;
    while (parent[x_root] != -1) {
        x_root = parent[x_root];
    }
    return x_root;
}

int Union(int x, int y, int parent[]， int rank[])
{
    int x_root = FindRoot(x, parent);
    int y_root = FindRoot(y, parent);

    if(x_root == y_root) {
        return 0;
    }
    else {
        // parent[x_root] = y_root;
        if ( rank[x_root] > rank[y_root] ) {
            parent[y_root] = x_root;
        }
        else if ( rank[x_root] < rank[y_root] ) {
            parent[x_root] = y_root;
        }
        else {
            parent[x_root] = y_root;
            ++rank;
        }
        return 1;
    }
}

int main()
{
    int parent[VERTICES] = {0};
    int rank[VERTICES] = {0};
    int edges[6][2] = {
        {0, 1}, {1, 2}, {1, 3},
        {2, 4}, {3, 4}, {2, 5}
    };

    Init(parent, rank);

    for(int i = 0; i < 6; ++i) {
        int x = edges[i][0];
        int y = edges[i][1];

        if(Union(x, y, parent, rank) == 0) {
            printf("Cycle detected!\n");
            exit(0);
        }
    }

    printf("No cycle found.\n");

    return 0;
}

上面是一种路径压缩的思路，即根据 rank 数组，将较矮的树连接到较高的树上。

也有另一种路径压缩的方法，如下

int FindRoot(int x, int parent[])
{
    int x_root = x;

    while( x != parent[x]) {
        x = parent[x];    // 此时 x 为根节点
    }

    // 进行路径压缩, 把所有非根节点的父节点都改为x
    while(-1 != parent[x_root])
    {
        int z = x_root;           // 先记录该节点
        x_root = parent[x_root];  // a指向父节点
        parent[z] = x;            // 修改子节点的父亲
    }
    return x;
}