决策树
决策树是一种基本的分类与回归方法,此处主要讨论分类的决策树。
所构造的决策树是一棵多叉树,非叶子结点代表特征或者属性,叶子结点代表输出的类别的集合,有向边则代表一种选择。
决策树的学习本质上是从训练集中归纳出一组分类规则,得到与数据集矛盾较小的决策树,同时具有很好的泛化能力。
决策树的路径:从根节点开始到叶节点的结束的一个结点序列。
决策树的单元:单元就是特征空间被决策树划分后的子空间,每个单元互不相交,有几个叶子结点,就代表划分了几个单元,
单元和叶子结点一一对应,即单元和根到叶子节点的路径一一对应。单元内的所有实例不一定都具有相同的类别,后面会介绍
划分单元的评价标准。
决策树与条件概率分布:这个概率分布中的条件指的是给定的特征,可以是全部的特征,也可以是局部的特征,于是样本
空间就被缩小了,变成了给定条件下的某个单元,每个单元上都定义了一个条件概率分布,那整个决策树的条件概率分布就
由各个单元的条件概率分布组成。每个单元的条件概率分布定义如下:
$$P(Y | X^{(1)} = a,X^{(2)} = b, \cdots )$$
举个例子:一个决策树某一叶子结点对应的单元包含了 $10$ 个输入实例,其中有 $8$ 个正类 $1$,$2$ 个负类 $-1$,那么在
给定的特征条件下(到达该叶子结点的特征条件)有
$$P(Y = +1 | X^{(1)} = a,X^{(2)} = b, \cdots ) = \frac{4}{5} \\
P(Y = -1 | X^{(1)} = a,X^{(2)} = b, \cdots ) = \frac{1}{5}$$
当给了一个新的输入,假如搜索决策树时到达了这一个叶子结点,那么可根据条件概率认为它是一个正类。
如果决策树能根据特征将所有的样本完全划分,即分完后每个单元中的所有实例都属于同一个类别,那也就不存在什么条件概率了,
因为概率都是 $1$ 了,但像这样分的太过精细可能会导致过拟合问题,因此还需要进行剪枝,剪枝后单元内就会有不同类别的实例,
这时就需要用条件概率分布来判断了,输出最大概率所对应的类别。
特征选择
自信息量:如果待分类的事物可能划分在多个类之中,则符号 $x_{i}$ 的自信息量定义为
$$l(x_{i}) = -\log_{2} p(x_{i})$$
式子中的对数可以以 $2$ 为底,也可以以 $e$ 为底。
其中,$p(x_{i})$ 为该分类的概率。从式子中可以看出,事件发生的概率越大,它的自信息量越少,这是符合实际的,一件事情越容
易发生,那人们便见怪不怪,习以为常了,谈不上有什么价值,但一件事情很难发生,比如中了 $1000$ 万彩票,那这件事就很有价值,
就值得人们去分析,探究。
熵:随机变量不确定性的度量,为自信息量的期望,定义为
$$H(X) = -\sum_{i=1}^{n}p(x_{i})\log_{2} p(x_{i})$$
$n$ 为分类数目,熵只依赖于 $X$ 分布,与 $X$ 的取值无关。熵是随机变量的函数。
为什么这个函数能度量随机变量的不确定性呢?
假设随机变量只取两个值 $1,0$,如果 $p(x=1) = 1,p(x=0) = 0$,那这个试验还有不确定性吗?显然没有,板上钉钉。那如果
每个试验结果发生的概率均为 $0.5$ 呢?因为每种结果发生的可能性相同,无法认为谁比谁更可能发生,所以此时的不确定性应
该是最大的,函数 $H(p) = -p\log_{2}(p) - (1-p)\log_{2}(1-p)$ 正是具有这种特性,它的对称轴为 $p = 0.5$,图像如下:
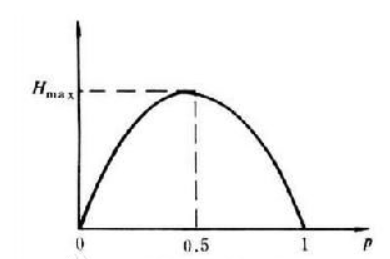
那三元、四元呢?肯定也是这样的特性,可以用 matlab 画画图像看看,这里不再赘述。
条件熵:已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性。
$$H(Y | X) = \sum_{i=1}^{n}P(X = x_{i})H(Y | X = x_{i}) = \sum_{i=1}^{n}\left ( -p(x_{i})\sum_{j=1}^{m}p(y_{j} | x_{i}) \log_{2} p(y_{j} | x_{i}) \right ) = -\sum_{i=1}^{n}\sum_{j=1}^{m}p(x_{i},y_{j}) \log_{2} p(y_{j} | x_{i})$$
因为条件熵中 $X$ 也是一个变量,则需要先对变量 $X$ 取每个值,$n$ 为 $X$ 取值的个数,去每个值都有概率,每个值取完后,$Y$ 的样本空间
都会被压缩,得到对应的子空间,这个条件熵就是:$X$ 各取值概率和对应的 $Y$ 样本子空间(孩子节点)混乱程度的乘积和。
注:熵和条件熵都是针对全体的,如果计算它们的概率由数据估计(特别是极大似然估计)得到,那么对应的结果分别称为经验熵和经验条件熵。
信息增益:它是相对于特征而言的,输入特征向量中每个坐标轴都是一个随机变量,不妨设其中一个特征所对应的随机变量为 $X$,实例输出所对应
的随机变量为 $Y$,则特征 $X$ 对输出变量 $Y$ 的信息增益 $g(Y,X)$,定义为
$$g(Y,X) = H(Y) - H(Y|X) = H(Y) - \sum_{i=1}^{n}P(X = x_{i})H(Y_{i})$$
其中 $Y_{i}$ 是指特征 $X$ 取某一个具体值 $x_{i}$ 后对应的样本子集,比如身高这一特征,就可以取青年、中年和老年,$n$ 为该特征所有可能取值。
信息增益比:以信息增益作为划分训练数据集的特征,偏向于原来就比较混乱的特征或者说取值较多的特征。于是做一个类似归一化的操作,即
$$g_{R}(Y,X) = \frac{g(Y,X)}{H(X)}$$
决策树生成算法
1. $ID3$ 算法
a. 从根结点(root node)开始,对结点计算所有可能的特征的信息增益,选择信息增益最大的特征作为结点的特征。
b. 由该特征的不同取值建立子节点,再对子结点递归地调用以上方法,构建决策树;直到所有特征的信息增益均很小或没有特征可以选择为止;
c. 最后得到一个决策树。
2. $C4.5$ 算法
与 $ID3$ 算法相似,但是做了改进,将信息增益比作为选择特征的标准,就不再赘述了。
决策树的剪枝
决策树生成算法递归的产生决策树,直到不能继续下去为止,这样产生的树往往对训练数据的分类很准确,但对未知测试数据的分类缺没有那么精确,
即会出现过拟合现象。剪枝就是从已经生成的树上裁掉一些子树或叶节点,并将其根节点或父节点作为新的叶子节点,从而简化分类树模型。
上面介绍的两个算法可以通过确定阈值的方式进行预剪枝,使得树不会那么深,那么宽。
这里介绍另一种树建立完成后再整体剪枝的方法,使用的损失函数如下
$$C_{\alpha}(T) = C(T) + \alpha |T|$$
其中,$|T|$ 表示树中叶子结点的个数,叶子节点数越多表示模型越复杂,泛化能力越差,$\alpha$ 是对树规模的一个惩罚,所以项
$\alpha |T|$ 用来衡量模型的复杂程度。
左边那一项用来衡量模型对训练集数据的拟合程度,这个仍使用熵来度量,每个叶子节点上的熵越小,代表损失越小,数据越整齐。
$$C(T) = \sum_{t=1}^{|T|}N_{t}H_{t}(T)$$
其中,$H_{t}(T)$ 表示每一个叶子节点上的熵,$N_{t}$ 表示这个叶子节点上的训练集实例个数,用它来做了一个权重,然后求和。
$CART$ 算法
这个算法不同于之前介绍的 $ID3,C4.5$,前两个算法可能是个多叉树,由特征的取值决定,而 $CART$ 算法是一个二叉树。
$CART$ 既能是分类树,又能是回归树。回归树的目的是根据一个对象的信息预测该对象的属性,并以数值表示。怎样得到这个输出值?一般
情况下使用中值、平均值或者众数进行表示。分类树的作用是通过一个对象的特征来预测该对象所属的类别。
分裂的目的是为了能够让数据变纯,使决策树输出的结果更接近真实值。那么 $CART$ 是如何评价节点的纯度呢?
1. 回归树
对于回归树采用的是平方误差的形式,这个误差取决于两个方面:
1)选取哪个特征以及哪个对应取值来划分样本,不同的特征以及不同的取值,所产生的孩子结点均不一样。
2)当产生了孩子节点后,由于输出 $Y$ 是连续型随机变量,不同方式产生的输出得到的误差不一样,比如输出可以是均值、中位数和众数等。
对与回归树的划分,最重要的就是确定每一次划分所取的特征 $j$ 和划分点 $s$,目标函数使用:
$$\min_{j,s}\left [ \min_{c_{1}} \sum_{x_{1} \in R_{1}(j,s)}^{}(y_{i}-c_{1})^{2} + \min_{c_{2}} \sum_{x_{1} \in R_{2}(j,s)}^{}(y_{i}-c_{2})^{2} \right ]$$
其中,$R_{1}(j,s)$ 属于某个结点划分后产生的左孩子,$R_{2}(j,s)$ 是右孩子。
初看这个式子感觉很奇怪,如果确定了以均值作为每个结点的输出属性,那平方损失就是一个定值,为什么还去求最小呢?
事实上,由于选择不同的 $c_{1},c_{2}$ 会产生不同的平方损失,所以这里的 $c_{1},c_{2}$ 并不是直接取均值,而是能使损失值最小的那个输出。
通过求导发现,$c_{1}$ 取为均值就能使 $\sum_{x_{1} \in R_{1}(j,s)}^{}(y_{i}-c_{1})^{2}$ 最小。当树建立完成之后,取每个叶子结点上输出的均值作为最后的输出。
2. 分类树
分类树采用基尼指数选择最优特征。假如有 $K$ 个类,样本点属于第 $k$ 类的概率为 $p_{k}$,则概率分布的基尼指数为
$$Gini(X) = \sum_{k=1}^{K}p_{k}(1-p_{k}) = 1 - \sum_{k=1}^{K}p_{k}^{2}$$
$$Gini(Y | X) = \sum_{i=1}^{n} P(X = x_{i})Gini(Y|X = x_{i}) = \sum_{i=1}^{n} P(X = x_{i})Gini(Y_{i})$$
和熵类似,基尼指数同样可以描述一个随机变量的不确定性的程度。
$CART$ 算法剪枝的流程如下:

这里还遗留一个证明:对于子树序列有 $\alpha_{1} < \alpha_{2} < ... < \alpha_{n} $。这个点还未想明白。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号