数据结构-Huffman树

一、定义

---

Huffma树，霍夫曼树 或 哈夫曼树，是一种带权路径和最短的树，也叫最优二叉树

一个树的带权路径和=每个叶子节点的带权路径长度之和

一个叶子节点的带权路径长度 = 节点权值 * 层高

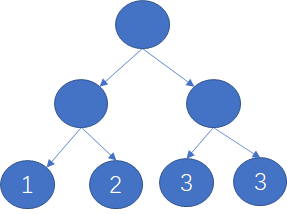
如下，节点1的带权路径长度=1*2（层高）=2

           整个树的带权路径长度=1*2 + 2*2 + 3*2 + 3*2 = 18

 

 

Huffman 树就是解决如下问题：

给定N个有权值的节点，如何构造一个二叉树使得树的带权路径之和 最短。

 

二、构造过程

---

 

原则：每次选择权值最小的两个节点构造树 

 

如有权值为1 2 3 4 共4个节点，

第一步：取最小的两个节点1 2作为左右子节点

父节点的权值=左右儿子节点权值之和

 

 

 

 

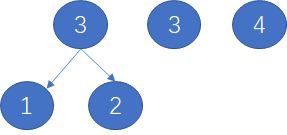
第二步：取 3 3两个节点作为左右儿子节点

 

 

 

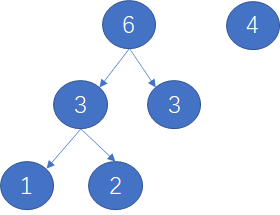
第三步：取4 6 两个字节作为左右儿子节点

 

 

 

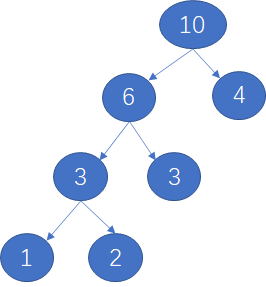
完成：次数即为Huffman树

 

三、场景

---

 

Huffman树常用于压缩算法。

如给定一串字符串，以每个字符出现的次数为权值，构建Huffman树

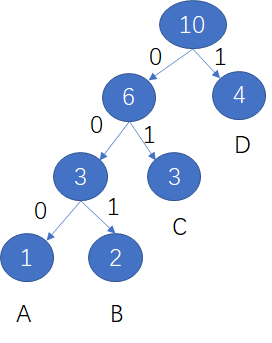
如A出现1次 B出现2次 C出现3次 D出现4次，构造的huffman树如下：

左边的路径用0标识，右边的路径用1标识，则编码如下：

A ： 000

B ：001

C ：01

D：1

次数出现越多的越靠近根节点，编码长度越短，这样就达到压缩的目的