搜索算法

一、分类

---

 

深度搜索：不断的搜索或计算子问题，直到某个分支结束，再回溯到上一个子问题，用途广泛

                  递归的实现就是一种深度搜索。

                  用的是栈的结构

广度搜索: 每次搜索下一个阶段的所有选项，都结束后 再来下一个阶段

                用于求最短路径之类的问题。

                用的是队列的结构

 

二、二叉树前序 后序 中序遍历

---

这3种都属于深度遍历。所谓前后中看的是树的中间节点出现的问题

 

如 二叉树

 

 

 

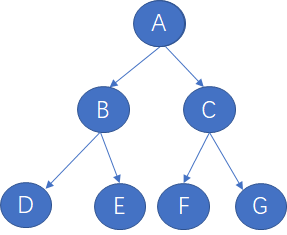
前序遍历： A B D E C F G

中序遍历:   D B E A F C G

后序遍历:   D E B F G C A

leecode上很多根据两种遍历 推断另一种遍历的算法题。

 

三、栈和队列的应用

---

 

栈: 可用ArrayDeque或LinkedList

      push和pop方法

队列: 可用ArrayDeque或LinkedList, ConcurrentLinkedQueue

     offer和poll方法

 

如求最短距离，我们把所有的子元素都放入队列中，依次再对子元素的子元素如队列，直到找到目标值

 

四、例子

---

 

走井子格问题，求从A到B总共有多少种走法，每个点只能走一遍

 

 

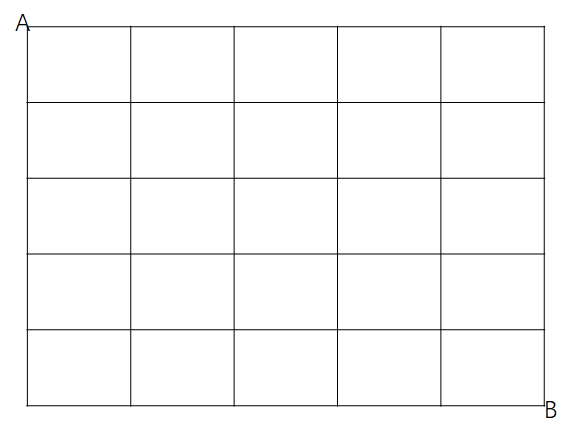
其实就是深度遍历，我们用递归的方式实现

定义f(i,j)表示点i,j到B的走法数目(假设共m行 n列)

f(i,j) = f(i+1,j) + f(i-1,j) + f(i,j-1) + f(i,j+1)

代码如下：

public class YfTest {
    private static int[][] nums = new int[5][6];

    // 标记访问记录 1表示已访问过此节点
    private static int[][] visited = new int[5][6];

    public static int f(int i, int j) {
        if (i < 0 || j < 0 || i >= nums.length || j >= nums[0].length) {
            return 0;
        }

        if (visited[i][j] == 1) {
            // 走过了就不能走了
            return 0;
        }

        if (i == nums.length - 1 && j == nums[0].length - 1) {
            // 一条路找到了
            return 1;
        }
        //标记
        visited[i][j] = 1;
        int sum = f(i + 1, j) + f(i - 1, j) + f(i, j - 1) + f(i, j + 1);
        // 回溯时还原
        visited[i][j] = 0;
        return sum;
    }

    public static void main(String[] args) {
        System.out.println("sum=" + f(0, 0));
    }
}

如果一个节点最多走2次 那只是visit条件的不同而已

注意回溯的时候需要消除标记