逻辑回归(Logistic Regression)
函数
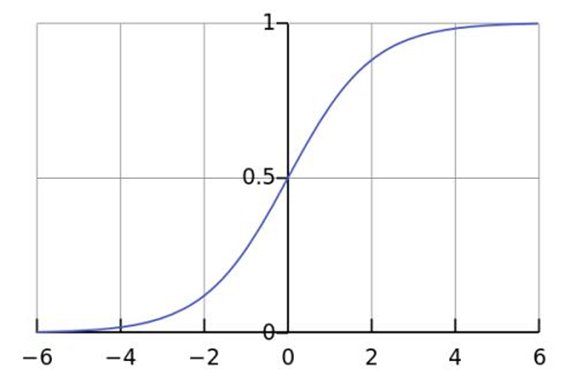
sigmod函数
\[y = \frac{1}{1+e^{-x}}
\]
原始条件概率
\[P(Y|X) = \frac{1}{1+e^{-(W^{T}x+b)}}
\]
对于一个二分类问题:
\[P(y=1|x,w) = \frac{1}{1+e^{-(W^{T}x+b)}}
\]
\[P(y=0|x,w) = \frac{e^{-(W^{T}x+b)}}{1+e^{-(W^{T}x+b)}} = 1-P(y=1|x,w)
\]
两个公式可以合并成:
\[P(y|x,w) = P(y=1|x,w)^y [1-p(y=1|x,w)]^{1-y}
\]
定义目标函数
假设我们的数据集\(D = \left \{ (x_i,y_i) \right \} ^{n}_{i=1} \qquad x_i\in R^d \qquad y_i \in \left \{ 0,1\right \}\)
而且我们定义了如下式子:
\[P(y|x,w) = P(y=1|x,w)^y [1-p(y=1|x,w)]^{1-y}
\]
我们需要最大化的目标函数:
\[\widehat{W}_{MLE}, \widehat{b}_{MLE} = argmax_{w,b}\prod_{i=1}^{n}p(y_i|x_i,w,b)
\]
注意:
\(\prod_{i=1}^{n}x_i = x_1*x_2*x_3...*x_n\)
\(\sum_{i=1}^{n} = x_1+x_2+x_3...+x_n\)
下面开始推导:
我们需要最大化的目标函数,
\[\widehat{W}_{MLE}, \widehat{b}_{MLE} = argmax_{w,b}\prod_{i=1}^{n}p(y_i|x_i,w,b)
\]
由于右边是连乘,可能会导致计算机计算的时候出现溢出,所以采取加对数log的处理方法,即
\[\widehat{W}_{MLE}, \widehat{b}_{MLE} = argmax_{w,b} \qquad log \qquad (\prod_{i=1}^{n}p(y_i|x_i,w,b))
\]
\[\widehat{W}_{MLE}, \widehat{b}_{MLE} = argmax_{w,b} \qquad \sum_{i=1}^{n} log \qquad p(y_i|x_i,w,b)
\]
注意:
\(\log_{}{xyz} = \log_{}{x}+ \log_{}{y}+ \log_{}{z}\)
对于最大化问题,我们一般取最小化,即
\[\widehat{W}_{MLE}, \widehat{b}_{MLE} = argmin_{w,b} \qquad -\sum_{i=1}^{n} log \qquad p(y_i|x_i,w,b)
\]
由于
\[P(y|x,w,b) = P(y=1|x,w,b)^y*[1-P(y=1|x,w,b)]^{1-y}
\]
所以
\[argmin_{w,b} \qquad -\sum_{i=1}^{n} log \qquad \left [ P(y=1|x,w,b)^y *[1-P(y=1|x,w,b)]^{1-y} \right ]
\]
\[argmin_{w,b} \qquad -\sum_{i=1}^{n} \qquad \left [ \qquad y *log P(y=1|x,w,b) +(1-y)log \left [ 1-P(y=1|x,w,b) \right ] \qquad \right ] \qquad
\]
我们令
\[P(y=1|x,w) = \frac{1}{1+e^{-(W^{T}x+b)}}=\sigma (W^{T}x+b)
\]
由此可得
\[argmin_{w,b} \qquad -\sum_{i=1}^{n} \qquad \left [ \qquad y *log \sigma (W^{T}x+b) +(1-y)log \left [ 1-\sigma (W^{T}x+b) \right ] \qquad \right ] \qquad
\]
\(\sigma (x) = \frac{1}{1+e^x}\)
\({\sigma (x)}' = \sigma (x)*[1-\sigma (x)]\)
\({\log_{}{x}}' = \frac{1}{x}\)
我们对\(W\)进行求导
\[\frac{\partial L(W,b)}{\partial W} = -\sum_{i=1}^{n} \left [ y_i*\frac{\sigma (W^Tx_i+b)*[1-\sigma(W^Tx_i+b)]}{\sigma (W^Tx_i+b)} *x_i + (y_i-1)*\frac{\sigma (W^Tx_i+b)*[1-\sigma(W^Tx_i+b)]}{1-\sigma (W^Tx_i+b)} *x_i \right ]
\]
\[\frac{\partial L(W,b)}{\partial W} = -\sum_{i=1}^{n}\left [ y_i*[1-\sigma(W^Tx_i+b)] *x_i + (y_i-1)*\sigma (W^Tx_i+b) *x_i\right ]
\]
\[\frac{\partial L(W,b)}{\partial W} = \sum_{i=1}^{n} \left [ \sigma(W^Tx_i+b) -y_i \right]*x_i
\]
使用梯度下降求解
经典问题
- 是否可以用线性回归来表示\(P(Y|X) = W^{T}x+b\) ? 为什么?
答:
不可以!
因为\(P(Y|X)\)为条件概率,那么既然是条件概率,那么就应该满足以下两个条件:
\[\begin{cases}
0\le P(Y|X) \le 1
\\
\sum P(Y|X) = 1
\end{cases}
\]
然而,很明显,
\[ -\infty \le W^{T}x + b \le +\infty
\]
也就是,
\[P(Y|X) ≠ W^{T}x + b
\]
\[(0,1) ≠ (-\infty ,+\infty )
\]
综上,不可以!
- 逻辑回归分类器是一个线性分类器吗?还是非线性分类器?为什么?
答:
是的!
下面的绿色的线就是决策边界
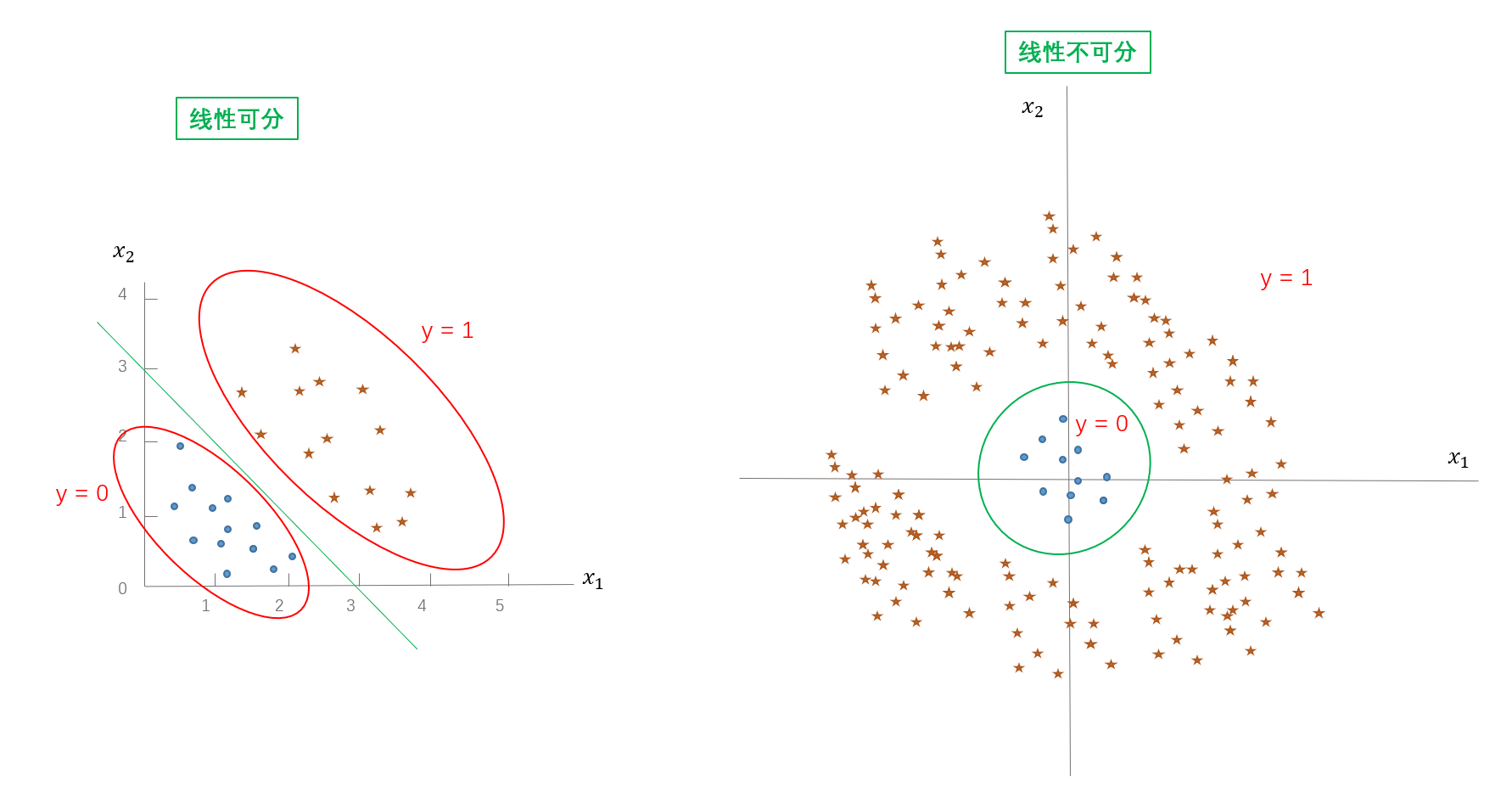
基于下面公式:
\[P(y=1|x,w) = \frac{1}{1+e^{-(W^{T}x+b)}}
\]
\[P(y=0|x,w) = \frac{e^{-(W^{T}x+b)}}{1+e^{-(W^{T}x+b)}}
\]
假设落在决策边界上的点,落在两边的概率是等同的
即:
\[\frac{P(y=1|x,w)}{P(y=0|x,w)} = 1
\]
得出
\[e^{-(W^{T}x+b)}=1
\]
两边加log
\[\log_{}{e^{-(W^{T}x+b)}} =\log_{}{1}
\]
得出
\[-(W^{T}x+b)=0
\]
最终
\[W^{T}x+b=0
\]
所以很明显逻辑回归的决策边界是一个线性的!
应用场景
- 贷款违约(会违约与不会违约)
- 广告点击(会点击与不会点击)
- 商品推荐(会购买与不会购买)
- 情感分析(正面与方面)
- 疾病诊断(阳性与阴性)
- other...


 浙公网安备 33010602011771号
浙公网安备 33010602011771号