模型评估方法

目录

• 准确率（Accuracy）
• 精确率(Precision)、召回率(Recall)和F1-score
  • 精确率
  • 召回率
  • F1-score

---

返回 我的研究方向(Research Interests)

---

准确率（Accuracy）

\[accuracy = \frac {\text {the number of samples}}{\text {the number of total samples}} \]

比如：在1000个样本中，有600个样本被我们的模型预测正确，那么我们认为该模型的准确率为

\[accuracy = \frac{600}{1000} = 0.6 \]

但是，当我们的 样本不均衡的时候，准确率就适合评估了！

样本不平衡：
意味着在我们收集的训练数据集中，假设我有两类不同的样本，比如说正样本和负样本，其中正样本可能占据的百分比可能是非常大，可能90%以上，负样本10%，这样的样本称之为不平衡

比如：在1000个人中，有5个人被认定为负样本，有995个人被认定为正样本，那么，由于样本不均衡，我们不做任何事就可以达到\(accuracy = \frac{995}{1000} = 0.995\)的准确率!这显然是不合理的。

精确率(Precision)、召回率(Recall)和F1-score

---

精确率

预测结果为正例样本中真实为正例的比例（查得准)

\[Precision = \frac{TP}{TP+FP} \]

召回率

真实为正例的样本中预测结果为正例的比例(查的全，对正样本的区分能力)。越高越好

\[Recall = \frac{TP}{TP+FN} \]

举例说明：

从上面的案例中可以看出，精确率和召回率两个是相斥的关系，一个提高，另一个就会下降

F1-score

反映了模型的稳健性，越高越好

\[F1 = \frac{2TP}{2TP+FN+FP} = \frac{2*Precision*Recall}{Precision+Recall} \]

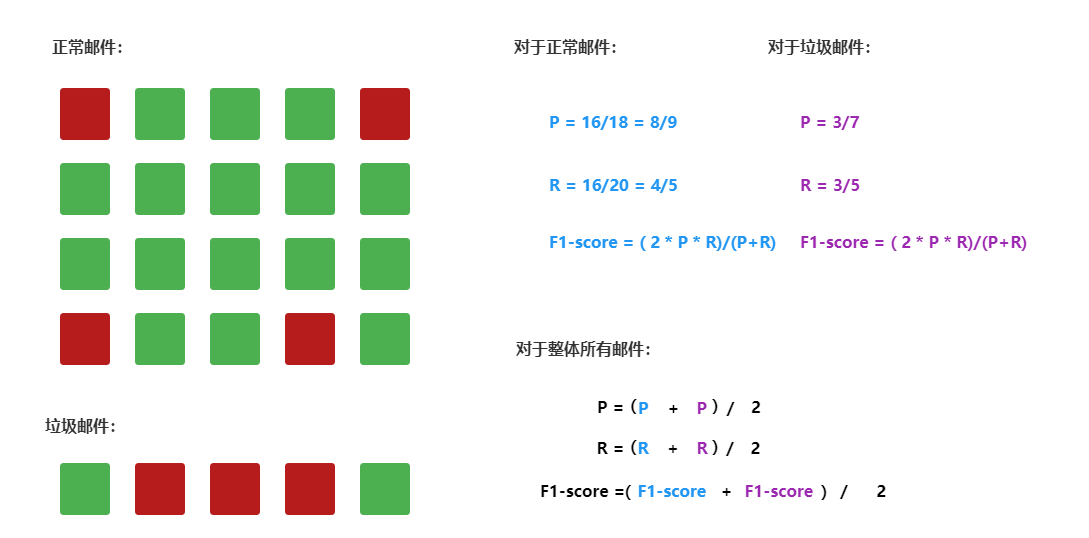
举例说明：