度中心性(Degrree centrality)-介数中心性(Betweeness centrality)-特征向量中心性( Eigenvector centrality)-k-壳与k-核

目录

• 无向网络节点重要性指标
  • 度中心性(Degrree centrality)
  • 介数中心性(Betweeness centrality)
  • 紧密中心性(Closeness centrality)
  • 特征向量中心性( Eigenvector centrality)
  • k-壳与k-核

---

返回 我的研究方向(Research Interests)

---

无向网络节点重要性指标

度中心性(Degrree centrality)

房地产行业有一个众所周知的黄金法则：地段、地段、还是地段。也就是说，一套房子的价值首先要看这套房子所在的地段。
把这一黄金法则搬到复杂网络上就成为：位置、位置、还是位置。也就是说，网络中一个节点的价值首先取决于这个节点在网络中所处的位置，位置越中心的节点其价值也越大。
这就是关于节点中心性指标的研究，它在不同的领域都具有重要意义。
例如:

• 在各种社会关系网络(如你的朋友圈子、BBS 和微博等在线社区)中，哪些是最活跃、最具影响力的人?
• 在艾滋病等疾病传播网络中，哪些人是最危险的?
• 在通信网络和交通网络中，哪些节点承受的流量最大?
• 当你在搜索引擎中输人一个关键词后，搜索引擎是如何知道哪些页面对你是最重要的，从而应该排在最前面显示给你?
  诸如此类的问题都与如何刻画节点在网络中所处的位置有关。

在社会网络分析中，常用“中心性(Centrality)"来判断网络中节点重要性或影响力。最直接的度量是度中心性(Degrree centrality)，即一个节点的度越大就意味着这个节点越重要。

这一指标背后的假设是：重要的节点就是拥有许多连接的节点。你的社会关系越多，你的影响力就越强。

度一个包含N个节点的网络中，节点最大可能的度值为N–1

在大多数社会网络中，结点的度遵守幂律分布——度很大的结点的数量只占一个网络中结点总数量的少部分，而度较小的结点的数量却占大多数。这些度较大的结点自然比同一网络中的其他结点发挥着更大的作用。因此，可以认为它们是更重要的节点。

节点的度中心性可以定义为:

\[C_D(v_i) = d_i = \sum_{j}A_{ij} \]

当需要比较不同网络中的结点的重要性时，可对度中心性的值实施规范化:
度为\(d_i\)的节点的归一化的度中心性值定义为:

\[C_{D}^{'}(v_i) = \frac{d_i}{N-1} \]

其中，N表示节点\(v_i\)所属网络中节点的总数量。

介数中心性(Betweeness centrality)

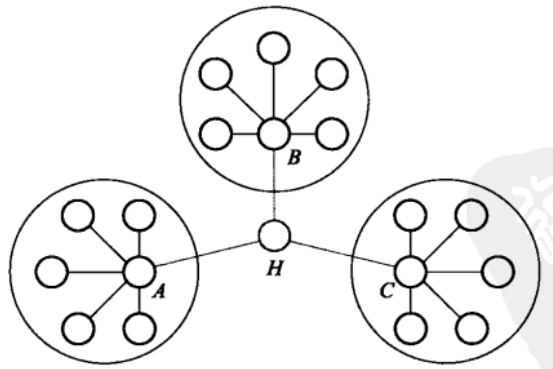
从每块中的任一节点到其他某块中的任一节点的最短路径必然要经过节点H。
这种以经过某个节点的最短路径的数目来刻画节点重要性的指标就称为介数中心性(Betweeness centrality)，简称介数(BC)。
也就是说，计算网络中任意两个节点的所有最短路径，如果这些最短路径中很多条都经过了某个节点，那么就认为这个节点的介中心性高。

节点的介数（betweenness)表示一个网络中经过该结点的最短路径的数量
在一个网络中，节点的介数越大，那么它在结点间的通信中所起的作用也越大

具体地，节点i的介数定义为：

\[BC_i= \sum_{v_s≠v_i≠v_t,s < t}\frac{σ_{st}(v_i)}{σ_{st}} \]

其中，
\(σ_{st}\)表示为从节点 s 到节点 t 的最短路径的总数量，
\(σ_{st}(v_i)\)表示这些最短路径中经过结点\(v_i\)的路径的数量。

介数的定义最早由Freeman于1977年给出"，它刻画了节点i对于网络中节点对之间沿着最短路径传输信息的控制能力。

从控制信息传输的角度而言，介数越高的节点其重要性也越大，去除这些节点后对网络传输的影响也越大。尽管在实际网络中，节点对之间的传输频率并不都一样，而且也并非所有的传输都是基于最短路径的，介数仍然近似刻画了节点对网络上信息流动的影响力。

举例：
一个包含9个用户和14个联系的社会网络。

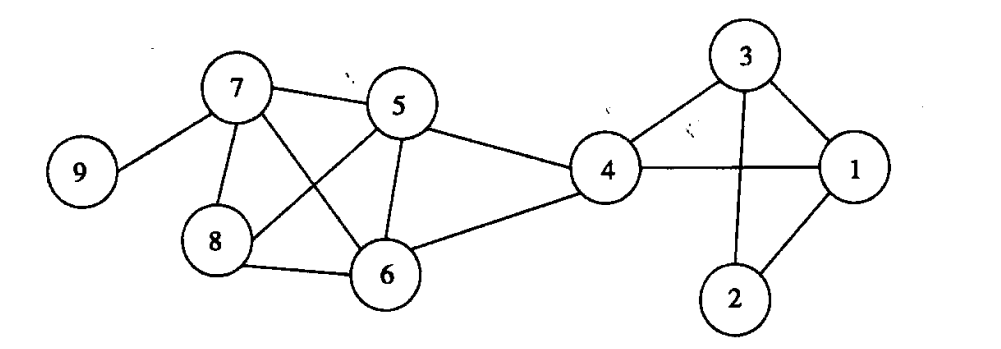
在图中所示的网络中有 \(σ_{19}\)=2。
这是因为在 节点1 和 节点9 之间有两条最短路径：1-4-5-7-9 和 1-4-6-7-9。
因此有 \(σ_{19}(4)\)=2 和 \(σ_{19}(5)\)=1，从而可以得到\(BC(4)\) = 1，\(BC(5)\) = 0.5。

这在图中体现为：从结点集合{1，2，3}到结点集合{5，6，7, 8}的所有最短路径都需要经过结点4。

紧密中心性(Closeness centrality)

点度中心性仅仅利用了网络的局部特征，即节点的连接数有多少，但一个人连接数多，并不代表他/她处于网络的核心位置。
紧密中心性和中介中心性一样，都利用了整个网络的特征，即一个节点在整个结构中所处的位置。

紧密中心性(Closeness centrality)也称接近中心性
紧密度中心性与非中心结点相比，一个中心结点应该能更快地到达网络内的其他结点。
即：如果节点到图中其他节点的最短距离都很小，那么它的接近中心性就很高。相比中介中心性，接近中心性更接近几何上的中心位置。

紧密度中心性用于评价一个结点到其他所有结点的紧密程度。

紧密度中心性需要计算一个结点到网络内其他所有结点的平均距离:

\[D_{avg}(v_i) = \frac{1}{N-1}\sum_{j≠i}^{n}g(v_i,v_j) \]

其中，N 表示结点\(v_i\)所属网络中的结点的总数量，\(g(v_i,v_j)\)表示结点\(v_i\)和\(v_j\)的最短距离(geodesic distance)。

这个平均距离可以理解为信息从结点\(v_i\)出发到达整个网络中所有结点所需要的时间。

通常，一个具有较高中心性的结点比其他结点更重要，因此，紧密度中心性的值定义为这个平均距离的倒数:

\[D_{c}(v_i) = [\frac{1}{N-1}\sum_{j≠i}^{n}g(v_i,v_j)]^{-1}=\frac{n-1}{\sum_{j≠i}^{n}g(v_i,v_j)} \]

举例：
一个包含9个用户和14个联系的社会网络。

结点对之间的距离(pairwise distance)可用下表表示：

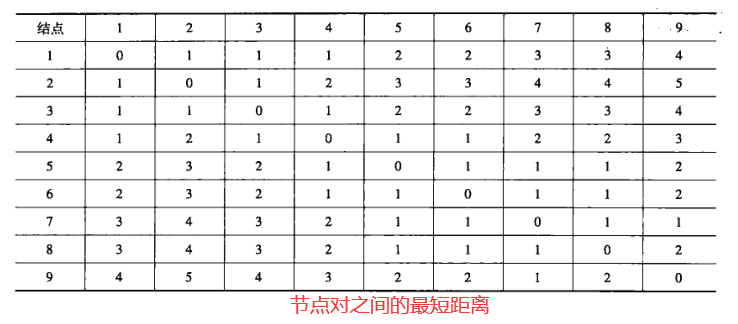
因此节点3和节点4的紧密度中心性的计算如下:

\[C_c(3) = \frac{9-1}{1+1+1+2+2+3+3+4}=\frac{8}{17}=0.47 \]

\[C_c(4) = \frac{9-1}{1+2+1+1+1+2+2+3}=\frac{8}{13}=0.62 \]

由于\(C_c(4)>C_c(3)\)，所以认为节点4比节点3更中心。

特征向量中心性( Eigenvector centrality)

特征向量中心性(Eigenvector centrality)的基本想法是:
一个节点的重要性既取决于其邻居节点的数量(即该节点的度)，也取决于其邻居节点的重要性。
换句话说，在一个网络中，如果一个人拥有很多重要的朋友，那么他也将是非常重要的。

特征向量中心性和度中心性不同，一个度中心性高即拥有很多连接的节点，特征向量中心性不一定高，因为所有的连接者有可能特征向量中心性很低。同理，特征向量中心性高并不意味着它的点度中心性高，它拥有很少但很重要的连接者也可以拥有高特征向量中心性。

记 \(x_i\) 为节点i的重要性度量值，那么，应该有

\[x_i = c\sum_{j=1}^{N}a_{ij}x_{j} \]

其中c为一比列常数，A=\((a_{ij})\) 是网络的邻接矩阵。记 \(x = [x_1 ~ x_2 ~ ... ~ x_N]^T\)

举例：
【1】
假设一个这样的图：

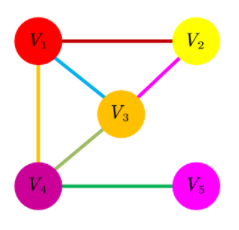
其对对应的邻接矩阵为：(邻接矩阵的含义是，如果两个节点没有直接连接，记为0，否则记为1)

\[A= \begin{bmatrix} 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 & 0\\ 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 &0 \end{bmatrix} \]

现在考虑 \(x\) ，一个 5x1 的向量，向量的值对应图中的每个点。在这种情况下，我们计算的是每个点的点度中心性（degree centrality），即以点的连接数来衡量中心性的高低。

\[x = \begin{bmatrix} 3\\ 2\\ 3\\ 3\\ 1 \end{bmatrix} \]

矩阵A乘以这个向量\(x\)的结果是一个 5x1 的向量：

\[A \times x= \begin{bmatrix} 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 & 0\\ 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 &0 \end{bmatrix}\begin{bmatrix} 3\\ 2\\ 3\\ 3\\ 1 \end{bmatrix} = \begin{bmatrix} 0\times3+1\times 2+1\times 3+1\times 3+0\times 1 \\ 1\times3+0\times 2+1\times 3+0\times 3+0\times 1 \\ 1\times3+1\times 2+0\times 3+1\times 3+0\times 1 \\ 1\times3+0\times 2+1\times 3+0\times 3+1\times 1 \\ 0\times3+0\times 2+1\times 3+0\times 3+0\times 1 \end{bmatrix}=\begin{bmatrix} 8\\ 6\\ 8\\ 7\\ 3 \end{bmatrix} \]

结果向量，可以理解为向量的第一个元素是用矩阵A的第一行去“获取”每一个与第一个点有连接的点的值（连接数，点度中心性），也就是第2个、第3个和第4个点的值，然后将它们加起来。

换句话说，邻接矩阵做的事情是将相邻节点的求和值重新分配给每个点。这样做的结果就是“扩散了”点度中心性。你的朋友的朋友越多，你的特征向量中心性就越高。

我们继续用矩阵A乘以结果向量。如何理解呢？
实际上，我们允许这一中心性数值再次沿着图的边界“扩散”。我们会观察到两个方向上的扩散（点既给予也收获相邻节点）。我们猜测，这一过程最后会达到一个平衡，特定点收获的数量会和它给予相邻节点的数量取得平衡。既然我们仅仅是累加，数值会越来越大，但我们最终会到达一个点，各个节点在整体中的比例会保持稳定。

现在把所有点的数值构成的向量用更一般的形式表示：

\[\begin{bmatrix} 0 & 1 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 & 0\\ 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 1\\ 0 & 0 & 0 & 1 &0 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4\\ x_5 \end{bmatrix} = \begin{bmatrix} 0\times x_1+1\times x_2+1\times x_3+1\times x_4+0\times x_5 \\ 1\times x_1+0\times x_2+1\times x_3+0\times x_4+0\times x_5 \\ 1\times x_1+1\times x_2+0\times x_3+1\times x_4+0\times x_5 \\ 1\times x_1+0\times x_2+1\times x_3+0\times x_4+1\times x_5 \\ 0\times x_1+0\times x_2+1\times x_3+0\times x_4+0\times x_5 \end{bmatrix} \]

我们认为，图中的点存在一个数值集合，对于它，用矩阵A去乘不会改变向量各个数值的相对大小。也就是说，它的数值会变大，但乘以的是同一个因子。用数学符号表示就是：

\[Mx=\lambda x \]

\[M\times \begin{bmatrix} x_1\\ x_2\\ x_3\\ ...\\ x_n \end{bmatrix} = \begin{bmatrix} \lambda x_1\\ \lambda x_2\\ \lambda x_3\\ ...\\ \lambda x_n \end{bmatrix} \]

满足这一属性的向量就是矩阵M的特征向量。特征向量的元素就是图中每个点的特征向量中心性。

【2】
一个包含9个用户和14个联系的社会网络。

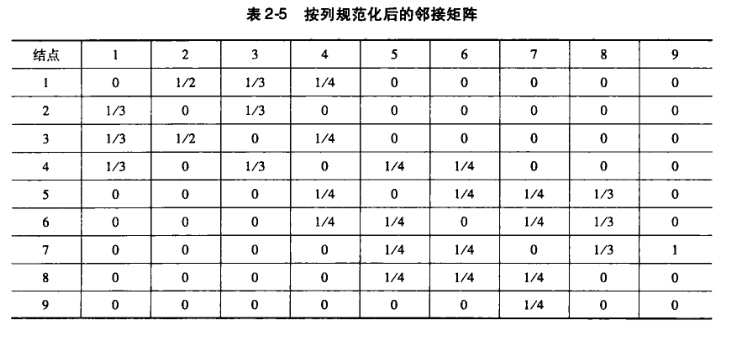
根据特征向量中心性的定义，就可以知道集合{4，5，6，7}中的结点的重要性在该网络中为最大。

k-壳与k-核

一种粗粒化的节点重要性分类方法，即k-壳分解方法(K-shelldecomposition method )。
不妨假设网络中不存在度值为0的孤立节点。这样从度中心性的角度看，度为1的节点就是网络中最不重要的节点。
如果我们把所有度值为Ⅰ的节点以及与这些节点相连的边都去掉会怎么样？
这时网络中可能又会出现一些新的度值为1的节点，我们就再把这些节点及其相连的边去掉，重复这种操作，直至网络中不再有度值为1的节点为止。
这种操作形象上相当于剥去了网络的最外面一层壳，
我们就把所有这些被去除的节点以及它们之间的连边称为网络的1-壳(1-shell)。
有时，网络中度为 0 的孤立节点也称为 0-壳(0-shell)。

在剥去了 1-壳 后的新网络中的每个节点的度值至少为2。
接下来我们可以继续剥壳操作，即重复把网络中度值为2的节点及其相连的边去掉直至不再有度值为2的节点为止。
我们把这一轮所有被去除的节点及它们之间的连边称为网络的2-壳(2-shell)。

依次类推，可以进一步得到指标更高的壳，直至网络中的每一个节点最后都被划分到相应的k-壳中，就得到了网络的k-壳分解。
网络中的每一个节点对应于唯一的 k-壳 指标\(K_s\)，并且 \(K_s\)-壳 中所包含的节点的度值必然满足 k≥\(K_s\)。

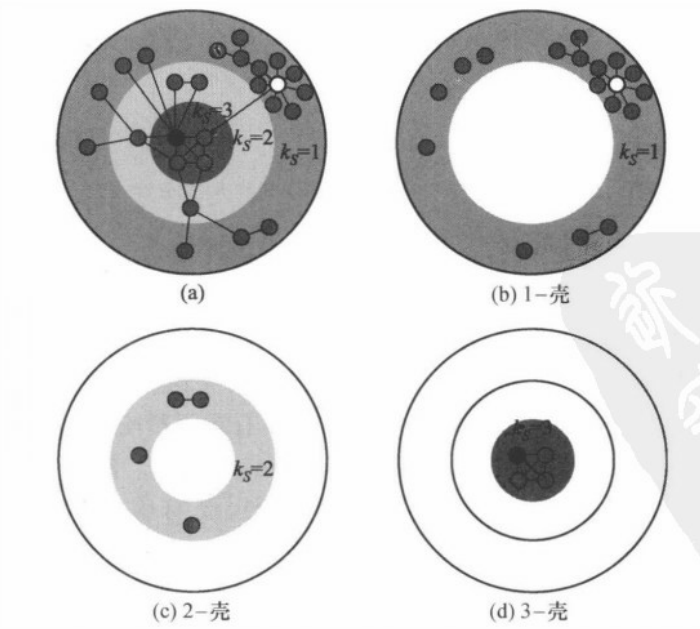
上图显示的是一个可分解为三层壳的简单网络。
图(b)—(d)分别显示了 1-壳 ，2-壳 和 3-壳 所包含的节点和边。
该网络中有两个度值最大的节点，即图中的黑色节点和白色节点，它们的度值都是 k =8，但是具有不同的\(K_s\)值：
黑色节点位于最里层，\(K_s\) =3；白色节点位于最外层\(K_s\) =1。

实际网络也会出现类似的情形：
度大的节点既可能具有较大的\(K_s\)值从而位于 k-壳分解 的核心内层，也有可能具有较小的\(K_s\)值而位于k-壳分解的外层，从而使得对于某些问题而言，度大的节点未必是重要的节点。

在得到一个网络的 k-壳 分解之后，我们
把所有\(K_s\)≥K 的 K-壳 的并集称为网络的k-核(K-core)
把指标\(K_s\)≤K 的 K-壳 的并集称为网络的k-皮(K-crust)
k-核的一个等价定义是:
它是一个网络中所有度值不小于 K 的节点组成的连通片。
基于这一定义，我们可以按照如下方法得到k-核:
首先去除网络中度值小于K的所有节点及其连边；如果在剩下的节点中仍然有度值小于K的节点，那么就继续去除这些节点，直至网络中剩下的节点的度值都不小于K。依次取K = 1,2,3，...，对原始网络重复这种去除操作，就得到了该网络的 k-核分解(k-core decomposition)。

对于一个连通网络，1-核实际上就是整个网络，(k + 1)-核一定是K-核的子集。

参考：

[1] 汪小帆,李翔,陈关荣.网络科学导论[M].北京:高等教育出版社,2012
[2] (美）唐磊（ Lei Tang）等著;文益民,闭应洲译.社会计算:社区发现和社会媒体挖掘[M].机械工业出版社:北京,2012
[3] https://blog.csdn.net/yyl424525/article/details/103108506