并查集判断二分图(tourist做法)

并查集判断二分图(tourist做法)

tourist代码：https://codeforces.com/contest/1702/submission/163478635

原理

一个图是二分图，当且仅当图中不含奇数环。

设二分图的两个点集为\(s1\)、\(s2\)，分别放在左边和右边。因为二分图的定义，边一定连接着一个\(s1\)的点和一个\(s2\)的点，那么形成环的首尾相接的边必然是\(s1\leftrightarrow s2 \leftrightarrow s1\leftrightarrow s2\dots\)

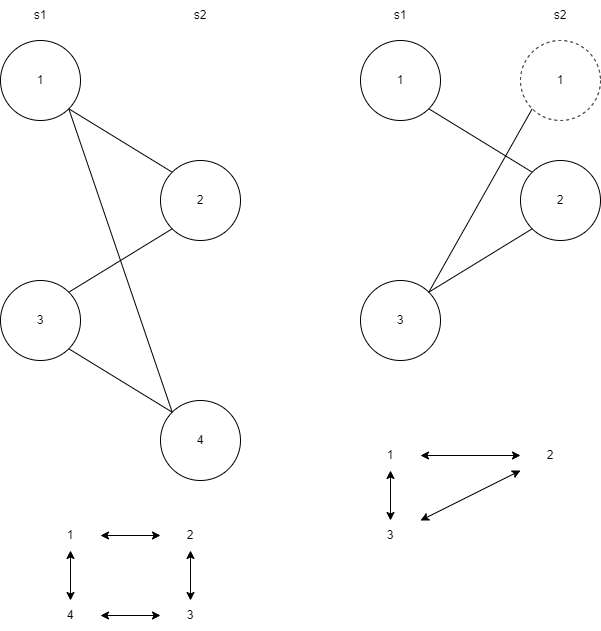
如图所示，如果是奇数环，不能二分图。因为从环的一个点出发，如果起点包含在\(s1\)中，经过奇数条边，又可以得出起点包含在\(s2\)中，矛盾。

并查集实现

将并查集大小开为点数的两倍，令\(1\sim n\)为集合\(s1\)，\(n+1\sim 2n\)为集合\(s2\)，两个集合各自都包含\(1\sim n\)号点。

将所有边连接的两个端点在并查集中合并，注意每条边连接一个\(s1\)的点和一个\(s2\)的点。也就是说，对每条边\(u\leftrightarrow v\)，将\(s1\)中的\(u\)与\(s2\)中的\(v\)合并，\(s1\)中的\(v\)与\(s2\)中的\(u\)合并。即uni(u, v+n); uni(v, u+n);。

出现奇数环时会使某个点\(p\)，在\(s1\)中的\(p\)与在\(s2\)中的\(p\)合并（如前面奇数环的图），即find(p) == find(p+n)。那就可以用并查集判断奇数环了。

最后会变成这样：

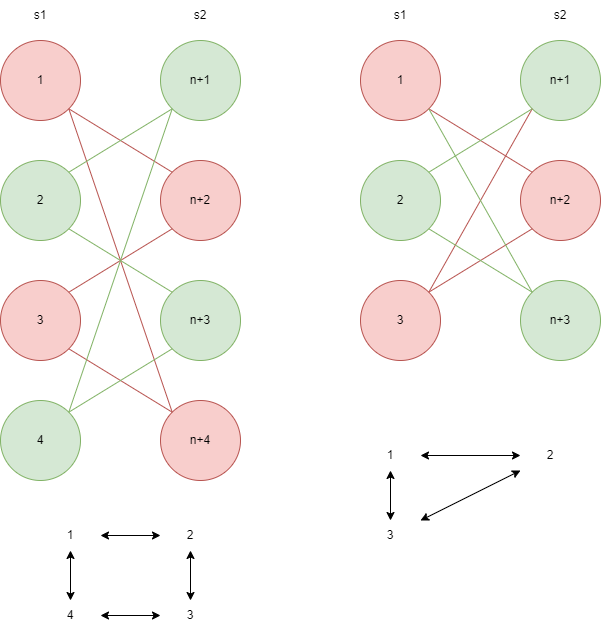
出现了一个对称的联通块，因为开了两倍的点，合并边的端点时也是对称操作的（因为是无向图，肯定要正反都做一次）。相当于原图中每个联通块二分为两个点集时，划为\(s1\)和\(s2\)一次，也划为\(s2\)和\(s1\)一次，总的两个集合\(s1\)\(s2\)也各自包含全部\(n\)个点。

偶数环的两个联通块是独立的。而奇数环的点全部合并在一起了（有绿边连接了红点，红边连接了绿点）。

代码

时间复杂度：\(O(m+n)\)

struct DSU {  //并查集模板
    vector<int> p;
    DSU(int n) : p(n + 1) { iota(p.begin(), p.end(), 0); }
    int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
    void uni(int x, int y) { p[find(x)] = find(y); }
    bool same(int x, int y) { return find(x) == find(y); }
};
struct Edge { int u, v; } edge[M];
bool check(int n, int m) {
    DSU dsu(n * 2);
    for (int i = 1; i <= m; ++i) {  //合并所有边的两个端点
        int u = edge[i].u, v = edge[i].v;
        dsu.uni(u, v + n), dsu.uni(u + n, v);
    }
    for (int i = 1; i <= n; ++i)  //判断是否有i与i+n在一个集合中
        if (dsu.same(i, i + n))
            return false;
    return true;
}