令人惊艳的算法——蒙特卡洛采样法
更多机器学习、编程、AI相关知识,欢迎关注我的公众号“图灵的猫”。后台回复“学习资料”,即可获得海量机器学习、深度学习书籍等免费PDF资源

原文转载自我的知乎
蒙特卡洛算法使用概率来求π(圆周率)和定积分,在不使用任何公式和特殊计算方法的前提下,实现小数点后多位的准确率,真的惊艳到我了。我第一次接触蒙特卡洛算法,是在做数据采样的时候,这个名字是20世纪40年代美国在第二次世界大战中研制原子弹的“曼哈顿计划”计划的成员乌拉姆和冯·诺伊曼首先提出。冯·诺伊曼用驰名世界的赌城—摩纳哥的Monte Carlo来命名。但其实早在1777年,法国数学家布丰提出用投针实验的方法求圆周率,就已经用到了蒙特卡罗法,只是那个时候并没有特别命名。
什么是蒙特卡洛法?
假如篮子里有1000个苹果,让你每次闭着眼睛找一个最大的,可以不限制挑选次数。于是,你可以闭着眼随机拿了一个,然后再随机拿一个与第一个比,留下大的,再随机拿一个,与前次留下的比较,又可以留下大的。循环往复这样,拿的次数越多,挑出最大苹果的可能性也就越大,但除非你把1000个苹果都挑一遍,否则你无法肯定最终挑出来的就是最大的一个。也就是说,蒙特卡洛算法是样本越多,越能找到最佳的解决办法,不过不保证是最好的,因为如果有10000个苹果的话,说不定就能找到更大的。也就是,通过大量随机样本,不使用任何公式和计算方法,得到所要计算的值。接下来,我们用4个例子一起来看看蒙特卡洛法的应用吧。
例子1:求10000个整数的中位数先从中抽取m个数,m<10000,把它们的中位数近似地看作这个集合的中位数。随着m增大,近似结果是最终结果的概率也在增大。
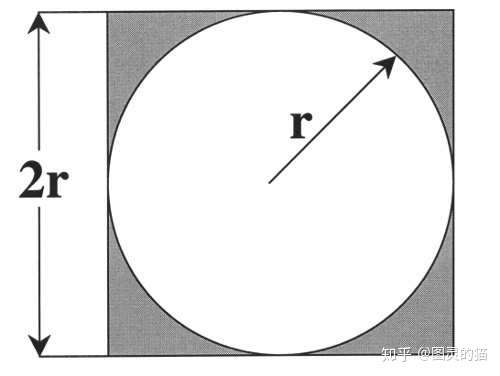
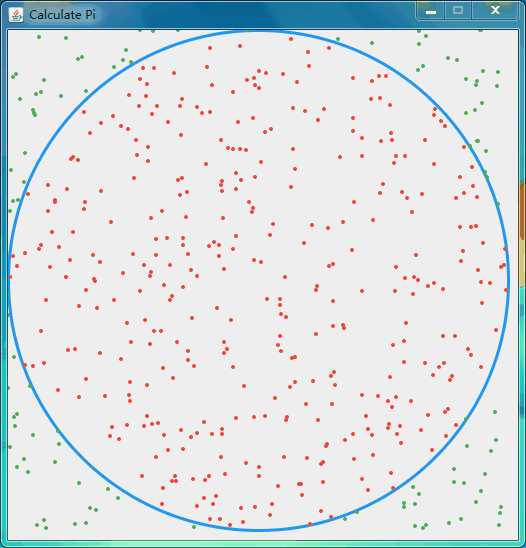
例子2:求圆周率给定一个边长为1的正方形,其内部有一个相切的圆根据高中知识,可以简单算出它们的面积之比是π/4。
当我们在(0,1)的范围内随机选择一个坐标(x, y)时,每个坐标点被选中的概率相等。则坐标落在直径为1的正方形中的圆的概率为:
由切比雪夫不等式可知,在生成大量随机点的前提下我们能得到尽可能接近圆周率的值。
现在,在这个正方形内部,随机产生10000个点(即10000个坐标对 (x, y)),计算它们与中心点的距离,从而判断是否落在圆的内部。
如果这些点服从均匀分布,那么圆内的点应该占到所有点的 π/4,因此将这个比值乘以4,就是π的值。通过R语言随机模拟30000个点,π的估算值与真实值相差0.07%。
例子3:设0≤f(x)≤1,求定积分设随机变量XX服从[0,1]上的均匀分布,则Y=f(X)的数学期望为
以估计J的值就是估计f(X)的数学期望值。由辛钦大数定律,可以用f(X)的观察值的均值取估计f(X)的数学期望。具体做法:先用计算机产生n个服从[0,1]上均匀分布的随机数:
对每一个xi,计算f(xi)。然后计算
其精确值和用蒙特卡洛法得到的模拟值如下:
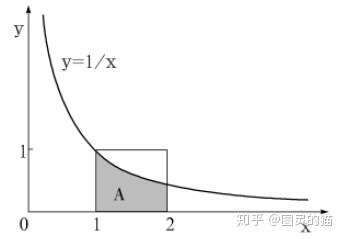
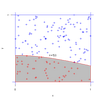
例子4:求自然底数e首先考虑如下积分接下来分别用蒙特卡洛积分和牛顿莱布尼兹公式计算,在蒙特卡洛方法中样本很多时,它们的值应该相等。利用蒙特卡洛方法,图像大致如下
上述积分的目的是求阴影部分的面积,所以先在所标矩形内取n对随机点
对于每一对
考察是否满足如下条件
假设满足上述条件的点有 m个,而全部的点有 n 个,所以得到近似公式为
而依据牛顿莱布尼兹公式可以得到
这两种方法结果应该是相等的,即有
更多机器学习、编程、AI相关知识,欢迎关注我的公众号“图灵的猫”。后台回复“学习资料”,即可获得海量机器学习、深度学习书籍等免费PDF资源~


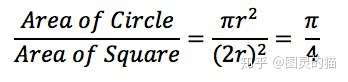
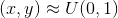
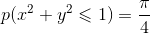
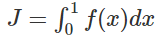
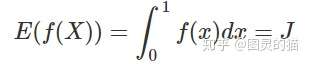
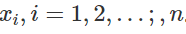
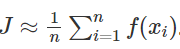

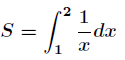
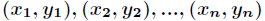
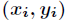
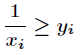
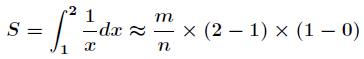

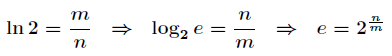

 浙公网安备 33010602011771号
浙公网安备 33010602011771号