不知道取什么名字的文章

## 1. 所有的三次函数的图像都是中心对称图形

数学老师上课讲的.

对于任意三次函数 $ f(x) = ax^3 + bx^2 + cx + d $，其关于 $ ( m, n ) $ 中心对称的充要条件是 $ g(x) = f(x + m) - n $ 为奇函数,只需找出 $ m,n $ 即可.

令 $ g( x ) = -g( -x ) $

$$ f( x + m ) - n = -(f( -x + m ) - n) $$

$$ f( x + m ) + f( -x + m ) = 2n $$

$$ a( x + m )^3 + b( x + m )^2 + c( x + m ) + d + a( -x + m )^3 + b( -x + m )^2 + c( -x + m ) + d = 2n $$

整理一下:

$$ ( 3ma + b )x^2 + m^3 a + m^2 b + mc + d = n $$

结果与 $ x $ 的值无关，令 $ 3ma + b = 0 $，所以有:

$$
\large\left\{\begin{matrix}
3ma + b = 0 \\
m^3 a + m^2 b + mc + d = n
\end{matrix}\right.
$$

解得:
$$

\large{ \left\{\begin{matrix}
m = -\frac{b}{3a} \\

n = \frac{2b^3}{27a^2} - \frac{bc}{3a} + d
\end{matrix}\right.}

$$

命题得证，且三次函数 $ f(x) = ax^3 + bx^2 + cx + d $ 关于 $ (-\frac{b}{3a}, \frac{2b^3}{27a^2} - \frac{bc}{3a} + d) $ 对称.

这个点在三次函数上，而且其左边三次函数增加量越来越小，其右边三次函数增加量越来越大——这个点是函数的 拐点.

所以也可以令 $ f(x) $ 的二阶导数为零时得出 $ m $ 值:

$$ f(x) = ax^3 + bx^2 + cx + d $$

$$ f'(x) = 3ax^2 + 2bx + c $$

$$ f''(x) = 6ax + 2b $$

令 $ f''(x) = 0 $，得到:

$$ x = -\frac{b}{3a} $$

即

$$ m = -\frac{b}{3a} $$

代入解析式，得到:

$$ n = \frac{2b^3}{27a^2} - \frac{bc}{3a} + d $$

## 2.正多面体只有五种: 正四面体，正六面体，正八面体，正十二面体，正二十面体

随眼看到的，觉得很神奇

前置知识: 欧拉公式: $ V - E + F = 2 $，其中 $ V $ 为多面体的顶点数，$ E $ 为多面体的棱数，$ F $ 为多面体的面数.

设每个点连接 $ m $ 条棱，每个面的多边形为正 $ n $ 边形.

则对于每个面来说有 $ n $ 条边，对于所有面的边数求和再除以 $ 2 $ 就是棱数 $ E $（相邻两个面共用一条棱）.

即:

$$ E = \frac{nF}{2} \qquad (1) $$

同理，对于所有点连接的棱数求和再除以 $ 2 $ 就是棱数 $ E $

即:

$$ E = \frac{mV}{2} \qquad (2) $$

又有欧拉公式:

$$ V - E + F = 2 \qquad (3) $$

联立 $ (1)(2)(3) $ 式，解得:

$$
\large
\left\{\begin{matrix}
V = \frac{4n}{2m + 2n - mn} \\
F = \frac{4m}{2m + 2n - mn} \\
E = \frac{2mn}{2m + 2n - mn}
\end{matrix}\right.

$$

由此，我们将一个拓扑学问题转化成了一个数论问题.

显然有 $ 2m + 2n - mn > 0 $，问题的关键就是找符合要求的整数 $ m,n $.

把曲线 $ 2m + 2n - mn $ 的图像画出来，标明对应 $ 2m + 2n - mn > 0 $ 的解集；

因为恒有 $ m,n \ge 3 $，于是再标明 $ m \ge 3 $ 和 $ n \ge 3 $ 的解集:


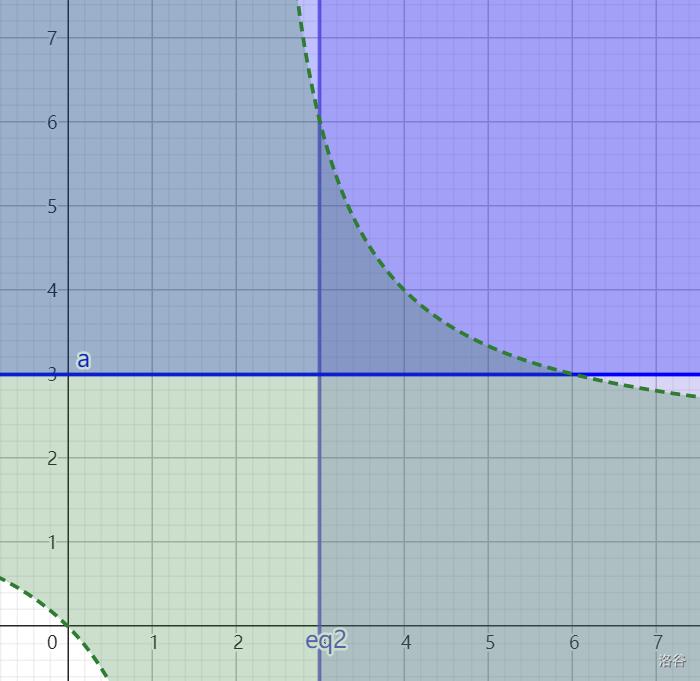
找出在共同解集中的点:


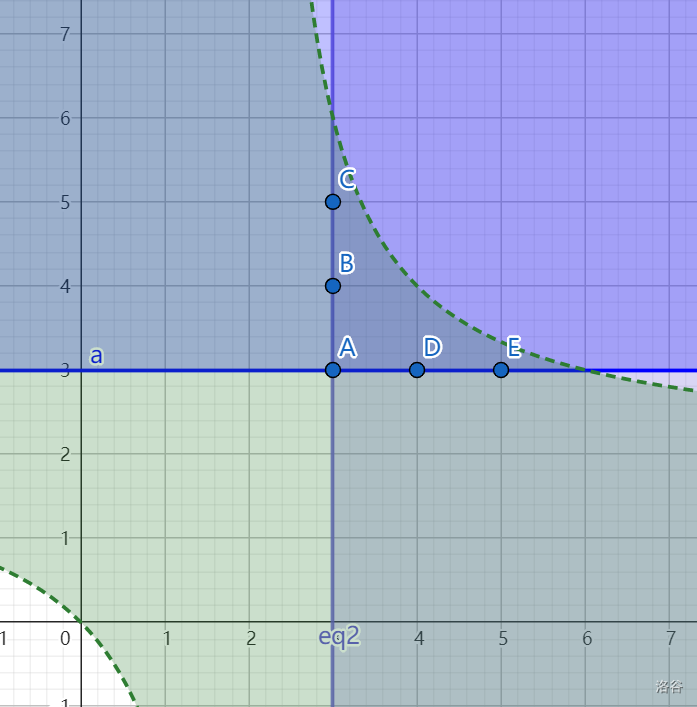
发现只有五个点，将其 $ m,n $ 值分别代入 $ F $ 的表达式，可以得出 $ F $ 的值分别为 $ 4, 6, 8, 12, 20 $.

## 3.椭圆的第 inf 个性质——斜率之比

对于椭圆 $ C:\frac{x^{2}} {a^{2}} + \frac{y^{2}} {b^{2}} $，过 $ x $ 轴某点 $ P(-x_0,0) $ 作直线交椭圆 $ C $ 与点 $ M,N $，则 $ \frac{k_{AM}} {k_{BN}} = \frac{a+x_0} {a-x_0} $（算了一节课算出来的），联立后方程为 $ (a^{2} k^{2} + b^{2} ) x^{2} + 2 a^{2} x_0 k^{2} x + a^{2} x_0 ^{2} k^{2} - a^{2} b^{2}=0 $，结果因式分解后为：

$$ \frac{(a+x_{0})(a^{2} x_{0} k^{2} - a b^{2} + x_{2} (k^{2} a^{2} + b^{2}))} {(a-x_{0})(a^{2} x_{0} k^{2} - a b^{2} + x_{2} (k^{2} a^{2} + b^{2}))} $$

当 $ -x_0 = -c $ 时，$ \frac{k_{AM}}{k_{BN}} = \frac{a+c}{a-c} = \frac{1+e}{1-e} $。