ABC311补题

A

小丑题

B

小丑题

C

_题意：给定一张 $n$ 个节点的图，每个节点有且仅有一条出边，求任意一条原图的环。It can be shown that a solution exists under the constraints of this problem.

显然原图不一定联通。

对于图的一个连通块，容易发现该连通块有且仅有一个环：

1. 若无环，则定有一点出度为 $0$，与题意矛盾

2. 若有超过两个环，则定有一点出度大于等于 $2$，与题意矛盾。

于是就可以从图上任意一点开始进行 dfs，一路标记，直至遇到已经 dfs 过的点（也就是找到了一个环），输出即可。

由于一个点有且仅有一条出边，所以在 dfs 的过程中一定会遇到环。

提交记录

D

小丑题，直接 dfs 即可。

细节挺多（好像也不是特别多），vis数组、dfs 函数需要比原来多维护一个方向信息。

提交记录

E

题意：在 $H$ 行 $W$ 列的矩形中有 $N$ 个特殊点，要求计算出矩形内所有不包含特殊点的正方形数量。

DP 好题。

设 $f_{i,j}$ 为 以 $(i,j)$ 为右下角端点的正方形数量。

如何转移？

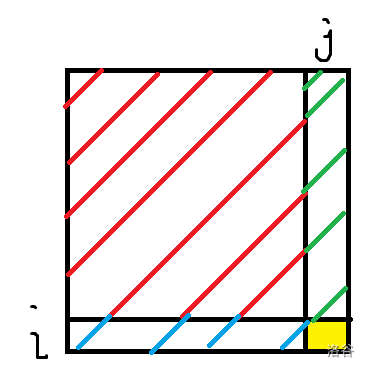
设一个合法正方形边长为 $a$。

则要求边长为 $a$ 的正方形包含的蓝色、红色、绿色区域不能有特殊点；

也就是说，如果有一方特殊点在该正方形内，边长为 $a$ 的以 $(i,j)$ 为右下角端点的正方形不存在（废话）。

观察到与最大合法正方形相关。

设最大合法正方形边长为 $a_0$；

那么 $f_{i,j}=a_0$。

于是问题转化为如何转移出 $a_0$，并且发现 $f_{i,j}$ 的另一含义是以 $(i,j)$ 为右下角端点的最大合法正方形边长。

容易发现，$a_0=min\{f_{i,j-1},f_{i-1,j},f_{i-1,j-1}\}+1$.

于是得到状态转移方程：

$f_{i,j}=min\{f_{i,j-1},f_{i-1,j},f_{i-1,j-1}\}+1$.

暴力 DP 即可。

提交记录

双倍经验 (从计数改成求最大值)

F

有 $n\times m$ 的网格，有一些点为 $1$，其余点为 $0$。可以将 $1$ 染色为 $0$。求合法染色方案数。

定义一个染色方案合法当且仅当对于任意整数 $i\in [1,n),j\in [1,m)$ 且 $(i,j)$ 为 $1$，有 $(i+1,j+1),(i+1,j)$ 为 $1$。

对 $998244353$ 取模。

根据题意，不难发现：

1. 如果一个点 $(i,j)$ 为 $1$，那么 $(i+1,j)$ 及以下的点均为 $1$。
2. 如果一个点 $(i,j)$ 为 $1$，那么 $(i-2,j-1)$ 及以上的点均为 $0$。

（对后续转移有大用）

设 $f_{i,j}$ 为以 $(i,j)$ 为黑色点且上方均为白色点时的方案数，$to{p}_j$ 为初始状态时第 $j$ 列最上方的黑色点的行坐标。

写出转移方程：

$f_{i,j}=\sum f_{k,j-1}$，其中$k\in max[\{1,i+1\},n],i\in [1,to{p}_j]$。

发现 $\sum$ 那坨东西可以用前缀和优化掉。

细节挺多，主要是各种边界条件。

提交记录

G

我不会，长大后再学习。

Ex

我不会，长大后再学习。

后记：

more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?more and more vegetable,what should i do?