CF1788C Matching Numbers 题解

题意简述

给定一整数 $ n $，每次从 $ [1,2n] $ 里面取出两个数加和放进新序列。要求 $ n $ 次操作后将新序列排序时，新序列为一个公差为 $ 1 $ 的等差数列。构造一组取数方案使得满足要求，若不存在输出 $ -1 $。

Sol

神奇构造题。

设如果存在合法方案，则排序后数列为 $ s = \{ s_i \} ,i \in [1,n] $。

首先考虑不合法的情况，根据样例可知显然所有 $ n $ 为偶数的情况是不合法的：

若 $ n $ 为偶数时存在合法解，则 $ \sum_{i = 1} ^ {2n} i = \frac{2n(2n + 1)}{2} = n(2n + 1) $。

$ s $ 中所有数的平均数为 $ \frac{n(2n + 1)}{n} = 2n + 1 $。

但实际上如果 $ n $ 为偶数，$ s $ 中所有数的平均数应该是小数点后有一位 $ 5 $。

矛盾，所以 $ n $ 为偶数时不存在合法解。

接下来只需要对每个奇数 $ n $ 构造一组通解即可。

可以举一个 $ n = 5 $ 的例子：

最终序列为 $ 9,10,11,12,13 $。

可构造 $ 9 = 3 + 6, 10 = 2 + 8, 11 = 1 + 10, 12 = 5 + 7, 13 = 4 + 9 $。

如下图：

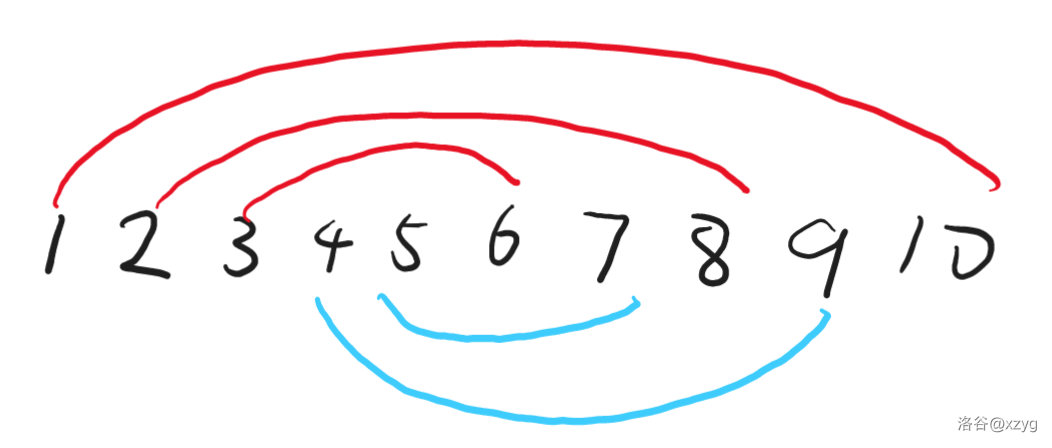
我们钦定 $ 1 $ 总是与 $ 2n $ 配对形成最终序列里最中间的数。

若 $ i \in [1, \lceil \frac{n}{2} \rceil] $，则可以将 $ i $ 与 $ 2n - 2(i-1) $ 即 $ 2n - 2i + 2 $ 配对。

若 $ i \in [\lceil \frac{n}{2} \rceil + 1, n] $，则可以将 $ i $ 与 $ 2n - 1 - 2(i - (\lceil \frac{n}{2} \rceil + 1) ) $ 即 $ 2n - 2i+ 2\lceil \frac{n}{2} \rceil + 1 $ 配对。

至于这样构造为什么是合法的，这里给出一个简单的证明：

对于每种情况，与 $ i $ 配对的数随着 $ i $ 的增大而减小，在每种情况内不会用重复的数，且该数一定在 $ [n+1, 2n] $ 范围内。

对于第一种情况，与 $ i $ 配对的数一定是偶数；对于第二种情况，与 $ i $ 配对的数一定是奇数。

两种情况互补，所有的数都没有重复的可能性，并且最终构造结果长度合法，所以该方案一定合法。

代码：

#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<algorithm> 
#define ll long long

using namespace std;

int main(){
    ll T;
    cin >> T;
    while(T--){
        ll n;
        cin >> n;
        if(n & 1){
            cout << "Yes\n";
            for(ll i = 1; i <= n/2 + 1; i++)
                cout << i << " " << 2 * n - 2 * i + 2 << '\n'; 
            for(ll i = n/2 + 2; i <= n; i++)
                cout << i << " " << 2 * n - 2 * i + 2 * (n + 1) / 2 + 1 << '\n';
        }else{
            cout << "No\n";
        }
    }
    return 0;
}