三角函数学习笔记

三角函数的定义

在初中范围内，三角函数是这样定义的：

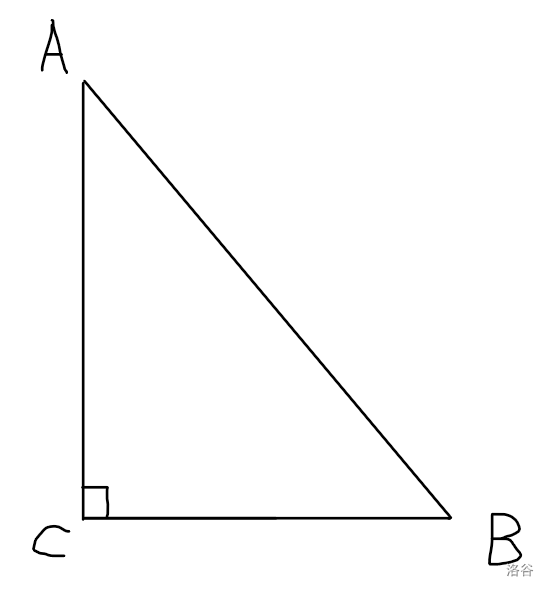
如图，在 \(Rt\triangle ABC\) 中，\(\angle C = 90^\circ\)，\(\angle A,\angle B\) 所对的边分别为 \(a,b\)，则：

\(\sin A = \dfrac{a}{c}\)，这个是 $\angle A $ 的正弦；

\(\cos A = \dfrac{b}{c}\)，这个是 $\angle A $ 的余弦；

\(\tan A = \dfrac{a}{b}\)，这个是 $\angle A $ 的正切；

$\sin A,\cos A,\tan A $ 是 $\angle A $ 的锐角三角函数。

所以，在初中没有钝角的三角函数

根据定义，得到 \(\sin B,\cos B,\tan B\) 的值：

\(\sin B = \dfrac{b}{c}\)

\(\cos B = \dfrac{a}{c}\)

\(\tan B = \dfrac{b}{a}\)

不难发现：

若 \(\angle A + \angle B = 90^\circ\),则：

\(\sin A = \cos B\)

\(\cos A = \sin B\)

\(\tan A \cdot \tan B = 1\)

同时，对于一个锐角 \(\alpha\)

\(\sin^2 \alpha + \cos^2 \alpha = \dfrac{a^2}{c^2} + \dfrac{b^2}{c^2} = \dfrac{a^2 + b^2}{c^2} = \dfrac{c^2}{c^2} = 1\)

$ \dfrac{\sin \alpha}{\cos \alpha} = \dfrac{\dfrac{a}{c}}{\dfrac{b}{c}} = \dfrac{a}{b} = \tan \alpha$

而在高中，三角函数是这样定义的：

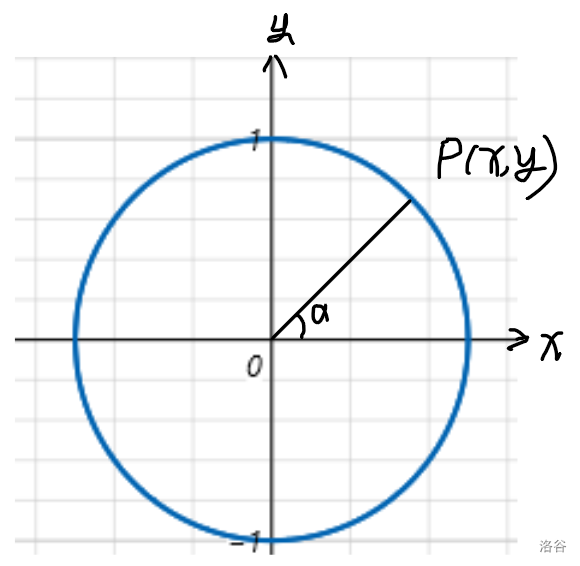
设 \(\alpha\) 是一个任意角，\(\alpha \in \mathbf R\)，它的终边 \(OP\) 与单位圆相交于点 \(P(x,y)\).

\(y\) 叫做 \(\alpha\) 的正弦函数:\(\qquad y = \sin \alpha\)

\(x\) 叫做 \(\alpha\) 的余弦函数:\(\qquad x = \cos \alpha\)

\(\frac{y}{x}\) 叫做 \(\alpha\) 的正切函数:\(\qquad \dfrac{y}{x} = \tan \alpha(x \ne 0)\)

将正弦函数、余弦函数和正切函数统称为三角函数.

通常将它们记为：

正弦函数 \(\quad y = \sin x,x \in \mathbf R\)

余弦函数 \(\quad y = \cos x,x \in \mathbf R\)

正切函数 \(\quad y = \tan x,x \ne \frac{\pi}{2}+k\pi(k \in \mathbf Z)\) \(\qquad\) （这里用的是弧度制）

当然，\(x\) 的范围就不仅仅局限于锐角了。

三角恒等变换

和差角公式

利用单位圆和旋转法：

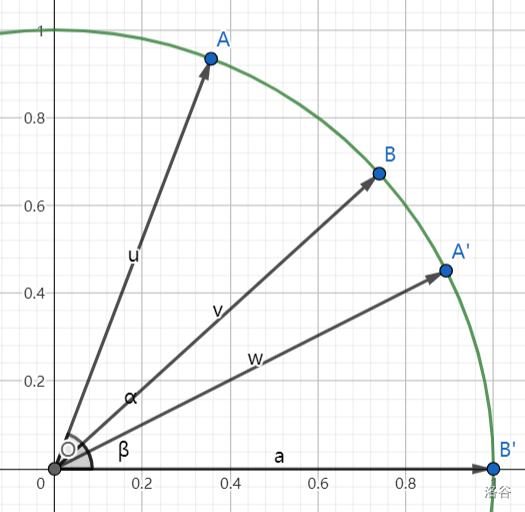
表示出 $ A,B,A' $ 的坐标：

$ A(\cos \alpha ,\sin \alpha),B(\cos \beta ,\sin \beta),A'(\cos (\alpha - \beta) ,\sin (\alpha - \beta)) $

由圆的旋转对称性可知： $ AB = A'B' $

所以有：

$ (\cos \alpha - \cos \beta)^2 + (\sin \alpha - \sin \beta)^2 = (\cos (\alpha - \beta) - 1)^2 + (\sin (\alpha - \beta) - 0)^2, $

$ \cos^2 \alpha + \cos^2 \beta - 2 \cos \alpha \cos \beta + \sin^2 \alpha + \sin^2 \beta - 2 \sin \alpha \sin \beta = \cos^2 (\alpha - \beta) - 2 \cos(\alpha - \beta) + 1 + \sin^2 (\alpha - \beta) $

整理，得：

$ \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta. $

由诱导公式可以得到其它三个和差角公式：

$ \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta, $

$ \sin(\alpha - \beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta, $

$ \sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta. $

根据三角函数的商数关系得到正切的和差角公式：

$ \tan(\alpha + \beta) = \frac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)} = \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin \beta} = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} $

$ \tan(\alpha - \beta) = \frac{\sin(\alpha - \beta)}{\cos(\alpha - \beta)} = \frac{\sin \alpha \cos \beta - \cos \alpha \sin \beta}{\cos \alpha \cos \beta + \sin \alpha \sin \beta} = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} $

二倍角公式

在和差角公式中，令 $ \beta = \alpha $，得到二倍角公式：

$ \sin 2\alpha = 2 \sin \alpha \cos \alpha, $

$ \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha, $

$ \tan 2\alpha = \frac{\sin 2\alpha}{\cos 2\alpha} = \frac{2 \sin \alpha \cos \alpha}{\cos^2 \alpha - \sin^2 \alpha} = \frac{2 \tan \alpha}{1 - \tan^2 \alpha} $

对 $ \cos 2\alpha $ 简单变换：

$ \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = 2\cos^2 \alpha - 1 = 1 - 2 \sin^2 \alpha. $

降幂公式/半角公式

根据连等式 $ \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = 2\cos^2 \alpha - 1 = 1 - 2 \sin^2 \alpha $，则有：

$ \cos \alpha = 2\cos^2 \frac{\alpha}{2} - 1 = 1 - 2 \sin^2 \frac{\alpha}{2}. $

用 $ \cos \alpha $ 表示 $ \cos \frac{\alpha}{2},\sin \frac{\alpha}{2},\tan \frac{\alpha}{2}$得到：

$ \cos \frac{\alpha}{2} = \pm \sqrt{\frac{1 + \cos \alpha}{2}} $

$ \sin \frac{\alpha}{2} = \pm \sqrt{\frac{1 - \cos \alpha}{2}} $

$ \tan \frac{\alpha}{2} = \frac{\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} = \pm \frac{ \sqrt{\frac{1 - \cos \alpha}{2}}}{\sqrt{\frac{1 + \cos \alpha}{2}}} = \pm \sqrt{\frac{1 - \cos \alpha}{1 + \cos \alpha}} $